关于二进制

读《程序是怎样跑起来的》

用二进制表示计算机信息的原因

 计算机内部是由IC（集成电路）这种电子部件构成的。CPU和内存也是IC的一种，IC有几种不同的形状，有的像一条黑色的蜈蚣，在其两侧有数个乃至数百个引脚；有的则像插花用的针盘，引脚在IC内部并排排列着。IC的所有引脚，只有直流电压0V和+5V两个状态。也就是说，IC的一个引脚，只能表示两个状态。

 IC的这种特性，决定了计算机的信息数据只能用二进制树来处理。由于1位（引脚）只能表示两个状态，所以二进制的计数方式就变成了0、1、10、11、100……这种形式。虽然二进制树并不是专门为IC而设计的，但是和IC的特性非常吻合。计算机处理信息的最小单位 —位，就相当于二进制中的一位。位的英文是bit。

 二进制的位数一般是8位、16位、32位……也就是8的倍数，这是因为计算机所处理的信息的基本单位是8位二进制数。8位二进制数被称为一个字节。字节是最基本的信息计量单位。位是最小单位，字节是基本单位。

 用字节单位处理数据时，如果数字小于存储数据的字节数（=二进制数的位数），那么高位上就用0填补。例如，100111这个6位二进制数，用8位（=1字节）表示时为00100111，用16位（=2字节）表示时为0000000000100111。奔腾等32位微处理器，具有32个引脚以用于信息的输入和输出。也就是说，奔腾一次可以处理32位（32位=4字节）的二进制数据信息。

 程序中，即使是用十进制数和文字等记录信息，在编译后也会转换成二进制数的值，所以程序运行时计算机内部处理的也是用二进制数表示的信息。

什么是二进制

 二进制的值转十进制的值，是将二进制数的各数位的值和位权相乘，然后将相乘的结果相加。

例如：

00100111（二进制数）

各位数的值和位权相乘，即：

$$(0\ast 2^7)+(0\ast 2^6)+(0\ast 2^5)+(0\ast 2^4)+(0\ast 2^3)+(0\ast 2^2)+(0\ast 2^1)+(0\ast 2^0)$$
结果等于：

39（十进制）

十进制转二进制：

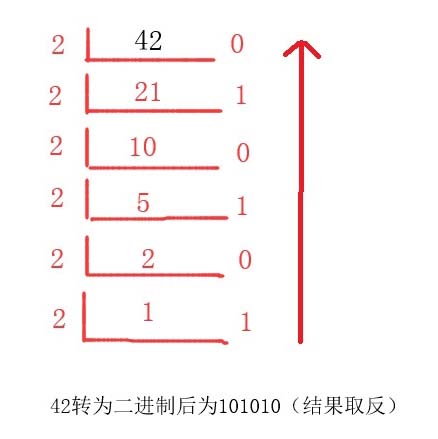
​ 位权的概念

 例如：十进制的39的各个数位的数值，并不是简单的3和9。3表示的是3x10=30，9表示的是9x1=9。这里和各个数位的数值相乘的10和1就是位权。同样，也适用于二进制数，即第1位是2的0次幂（=1），第2位是2的1次幂（=2），第3位是2的2次幂（=4），……这里的2是位权。

​ 基数的概念

 接上，十进制中，3x10中10是基数，二进制中2是基数。

移位运算和乘除运算的关系

移位运算是指将二进制数值的各位数位进行左右移位的运算，移位有左移（像高位方向）和右移（像低位方向）两种。

a=39;
b=a << 2;

例如，上面将a保存的十进制39左移两位后再将运算结果存储到变量b的C语言程序中。<<表示左移，>>表示右移。

由于移位运算是针对二进制数值的位操作，十进制39的移位，需要先将十进制的39转成二进制，然后在进行移位操作。左移两位后，右边空出来的低位要进行补0操作。注意，这个只适用于左移运算。具体流程如下：

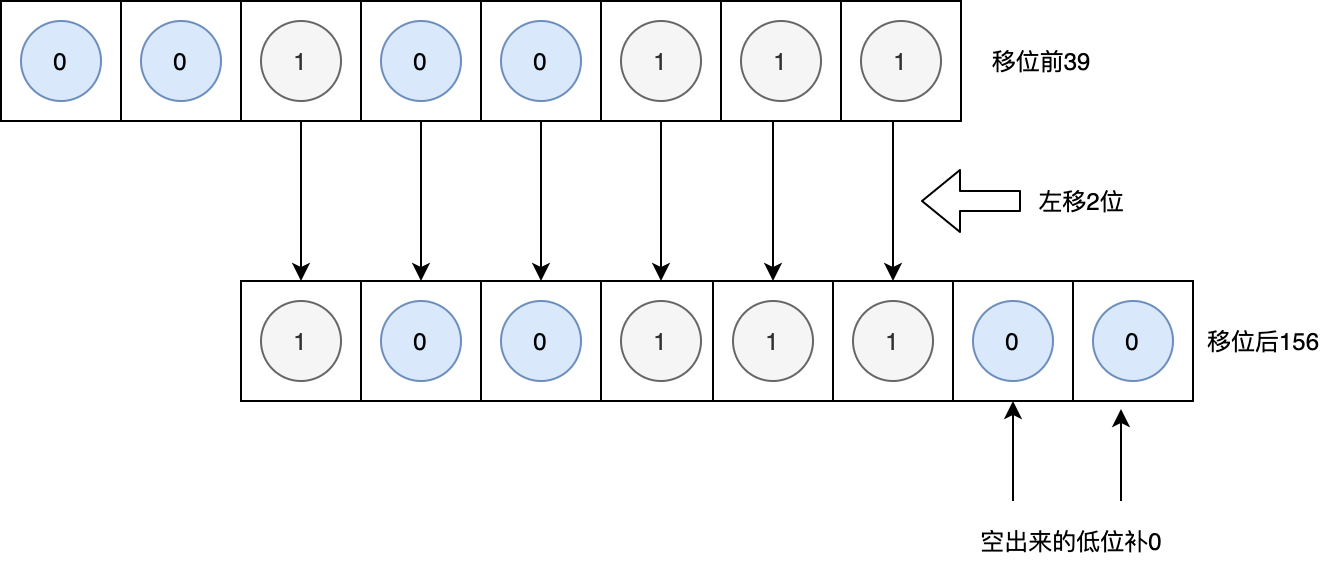
形象地说，移位运算就好比使用二进制表示的图片模式像霓虹灯一样左右流动的样子。

不过，移位运算也可以通过数位移动来代替乘法运算和除法运算，十进制数左移后会变成原来的10倍、100倍、1000倍……同样，二进制数左移后就会变成原来的2倍、4倍、8倍……反之，二进制数右移则会变成原来的1/2、1/4、1/8……。

关于补数

二进制中表示负数值时，一般会把最高位作为符号来使用，因此我们把这个最高位称为符号位。符号位是0时表示正数，符号位是1时表示负数。

那么-1用8位二进制数来表示的话是什么呢？可能很多人认为“1的二进制数00000001，因此-1就是10000001“，但这个答案是错误的，正确答案是11111111。

为什么这样呢？是因为计算机在做减法运算时，实际上内部时在做加法运算。用加法运算来现实减法运算，为此，在表示负数时就需要使用”二进制的补数“。补数就是用正数来表示负数。

为了获得补数，我们需要先将二进制数的各数位的数值全部取取反，然后再将结果加1。例如用8位的二进制表示-1时，只需求的1，也就是00000001的补数即11111110，然后+1得到1111111，即为十进制-1的值。

图示如下：

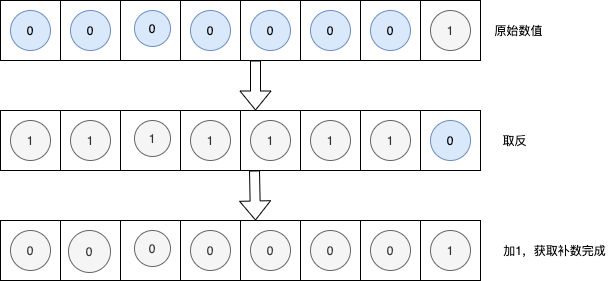
逻辑右移与算术右移

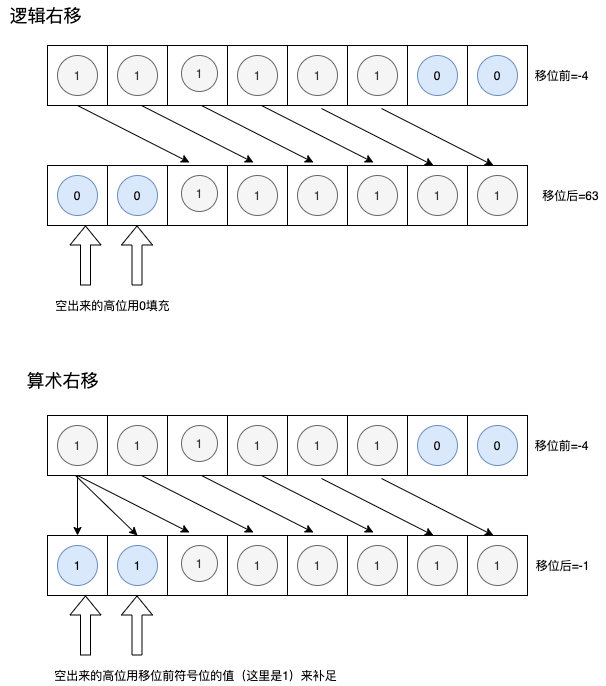
了解了补数，现在回到右移这个话题，右移不像左移（左移只需要在低位补0），右移移位后高位有补0和补1两种情况。当二进制数的值表示图形模式而非数值时，移位后需要在最高位补0。类似于霓虹灯往右滚动的效果。这种情况称为逻辑右移。

将二进制数作为带符号的数值进行运算时，移位后要在最高位填充移位前符号位的值（0或1）。这就称为算术右移。如果数值是用补数表示的负数值，那么右移后在空出来的最高位补1，就可以正确地实现1/2、1/4、1/8等数值运算。如果是正数，只需要在最高位补0即可。

例如，将-4（=11111100）右移两位。这时，逻辑右移的情况下结果就会变成00111111，也就是十进制数63，显然不是-4的1/4。而算术右移的情况下，结果就会变成11111111，用补数表示就是-1，即-4的1/4。

用二进制表示小数

由于计算机内部所有的信息都是以二进制数的形式来处理的，因此在这一点上，整数和小数并无差别。不过，使用二进制数来表示整数和小数的方法却有很大不同。

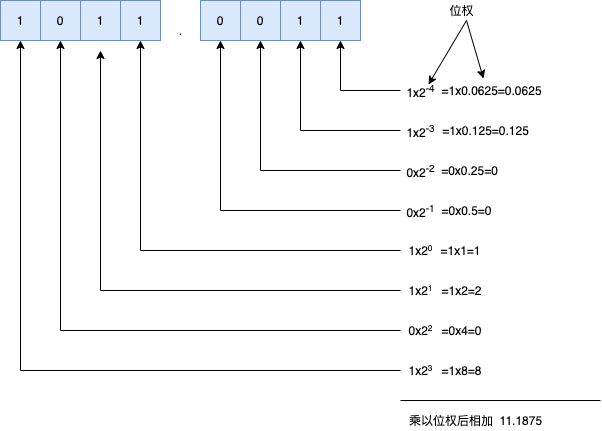
例如，把1011.0011这个有小数点的二进制数转换成十进制数，如下：

二进制数和十六进制数

在以位为单位表示数据时，使用二进制数很方便，但如果位数太多，看起来就比较麻烦。因此，在实际程序中，也经常会用十六进制数来代替二进制数。在C语言程序中，只需要在数值的开头加上0x就可以表示十六进制。

二进制的4位，正好相当于十六进制数的1位。例如，32位二进制数00111101110011001100110011001101用十六进制数来表示的话，就是3DCCCCCD这个8位数。

用十六进制数来表示二进制小数时，小数点后的二进制数的4位也同样相当于十六进制数的1位。不够4位时用0填补二进制数的低位即可。例如，1011.011的低位补0后为1011.0110，这时就可以表示为十六进制数B.6。

十六进制数的小数点后第1位的位权是16的-1次幂即1/16=0.0635。