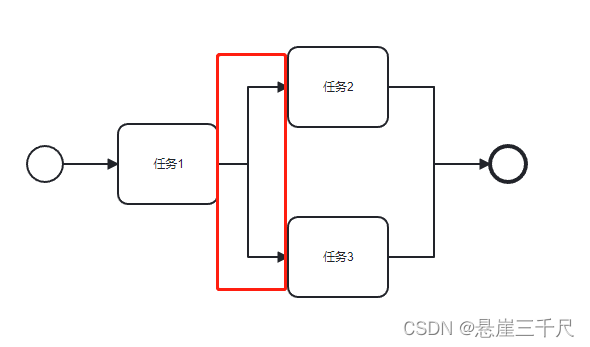
树:无回路 图:有回路
代码在最下面
邻接矩阵:重点:矩阵
(一)图的创建
存储方式
如图:

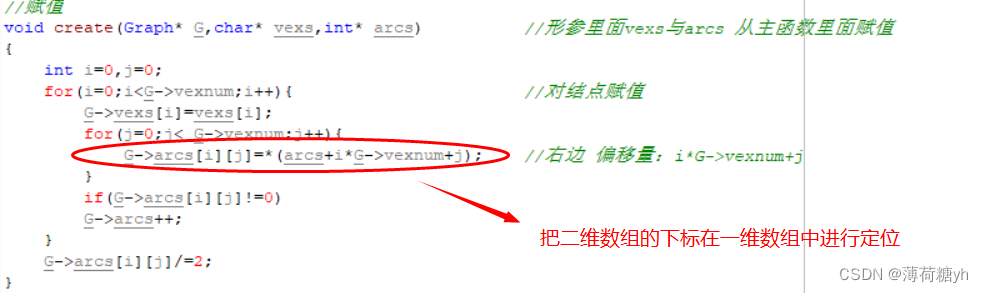
代码截图分析:顶点用一维数组存,边用两个点之间的值为0或1来表现,【比如说,你要看第一个结点与其他边的联系,就在上图的第一行看,这就好比二级指针的使用方法:指向不同行的一维数组。】

要点:二级指针的开辟空间方式

(二 图的遍历)
一)DFS:深度优先遍历
口诀:一条路走到黑;不到南墙不回头;撞墙之后再回头;回头之后再撞墙;
算法过程如下:
1.找一个结点
2访问这个结点可以访问的结点(深度优先),若下一个将要访问的结点都已经访问过了,退回去。
3.重复第二步,直到所有结点访问完毕。
G->arcs[index][i]==1&&!visited[i] //当前节点index与i有边,且没有被访问过就进入DFS并且遍历它。横着走是出度//【】G->arcs[index][i]==1表示index结点到i结点之间可以连,但是不能是连过的!!所以visited[i]==0才可以
for(i=0;i<G->vexnum;i++){
if(G->arcs[index][i]==1&&!visited[i]){
DFS(G,visited,i); //i作为index
}
}
二)bfs 广度优先遍历(有点像二叉树的层次遍历,也要用队列)
图是特殊的树,
图一转化为图二(画的比较像树):
核心算法:
Quene* Q=initQuene();
printf("%c",G->vexs[index]);
visited[index]=1;
inQuene(Q,index);
while(!isEmpty(Q)){
int i=outQuene(Q);
int j=0;
for(j=0;j<G->vexnum;j++){
//一次while只管一个顶点所连的其他子结点 ,这些结点在for里面进队
if(G->arcs[i][j]==1&&!visited[j]){
printf("%c",G->vexs[j]);
visited[j]=1;
inQuene(Q,j);
}
}
}
//图的创建 ,【邻接矩阵和无向图】
#include<stdio.h>
#include<stdlib.h>
#define MAXSIZE 5
typedef struct Quene{
int front;
int rear;
int data[MAXSIZE];
}Quene;
typedef struct Graph{
char* vexs;
int** arcs;
int vexnum;
int arcnum;
}Graph;
//初始化
Graph* initGraph(int vexnum)
{
int i=0;
Graph* G=(Graph*)malloc(sizeof(Graph));
G->vexs=(char*)malloc(sizeof(char)*vexnum);
G->arcs=(int**)malloc(sizeof(int*)*vexnum);
for(i=0;i<vexnum;i++){
G->arcs[i]=(int*)malloc(sizeof(int)*vexnum);
}
G->vexnum=vexnum;
G->arcnum=0;
return G;
}
//图的创建
void createGraph(Graph* G,char* vexs,int* arcs)
{
int i=0,j=0;
for(i=0;i<G->vexnum;i++){
G->vexs[i]=vexs[i];
for(j=0;j<G->vexnum;j++){
G->arcs[i][j]=*(arcs+i*G->vexnum+j);
if(G->arcs[i][j]!=0)G->arcnum++;
}
}
G->arcnum/=2;
}
//DFS
void DFS(Graph* G,int* visited,int index)
{
int i=0;
printf("%c\t",G->vexs[index]);
visited[index]=1;
for(i=0;i<G->vexnum;i++){
if(G->arcs[index][i]==1&&!visited[i]){
DFS(G,visited,i);
}
}
}
//对的初始化
Quene* initQuene()
{
Quene* Q=(Quene*)malloc(sizeof(Quene));
Q->front=Q->rear=0;
return Q;
}
//判断队满
int isFull(Quene* Q)
{
if((Q->rear+1)%MAXSIZE==Q->front)return 1;
else return 0;
}
//判断对空
int isEmpty(Quene* Q)
{
if(Q->front==Q->rear)return 1;
else return 0;
}
//入队
int inQuene(Quene* Q,int data)
{
if(isFull(Q))return 0;
else {
Q->data[Q->rear]=data;
Q->rear=(Q->rear+1)%MAXSIZE;
return 1;
}
}
//出队
int outQuene(Quene* Q)
{
if(isEmpty(Q))return -1;
else {
int i=0;
i=Q->data[Q->front];
Q->front=(Q->front+1)%MAXSIZE;
return i;
}
}
//BFS[广度优先]
void BFS(Graph* G,int* visited,int index)
{
Quene* Q=initQuene();
printf("%c",G->vexs[index]);
visited[index]=1;
inQuene(Q,index);
while(!isEmpty(Q)){
int i=outQuene(Q);
int j=0;
for(j=0;j<G->vexnum;j++){ //一次while只管一个顶点所连的其他子结点 ,这些结点在for里面进队
if(G->arcs[i][j]==1&&!visited[j]){
printf("%c",G->vexs[j]);
visited[j]=1;
inQuene(Q,j);
}
}
}
}
int main(){
int i=0;
Graph* G=initGraph(5);
int* visited=(int*)malloc(sizeof(int)*G->vexnum);
for(i=0;i<G->vexnum;i++)visited[i]=0;
int arcs[5][5]={
0,1,1,1,0,
1,0,1,1,1,
1,1,0,0,0,
1,1,0,0,1,
0,1,0,1,0
};
createGraph(G,"ABCDE",(int*)arcs);
DFS(G,visited,0);
printf("\n");
for(i=0;i<G->vexnum;i++)visited[i]=0;
BFS(G,visited,0);
printf("\n");
return 0;
}