OpenSSL

常用证书生成工具包括三个：ssh-keygen、cfssl、openssl。这里介绍 OpenSSL , OpenSSL 是一个开源项目，其组成主要包括一下三个组件：

openssl：多用途的命令行工具

libcrypto：加密算法库

libssl：加密模块应用库，实现了ssl及tls

openssl可以实现：秘钥证书管理、对称加密和非对称加密 。

openssl实现对称加密

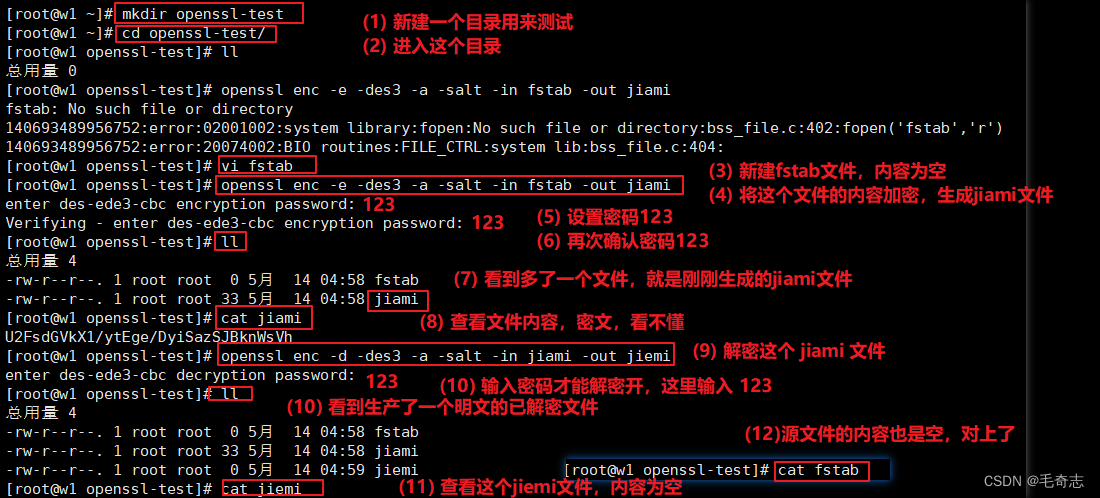
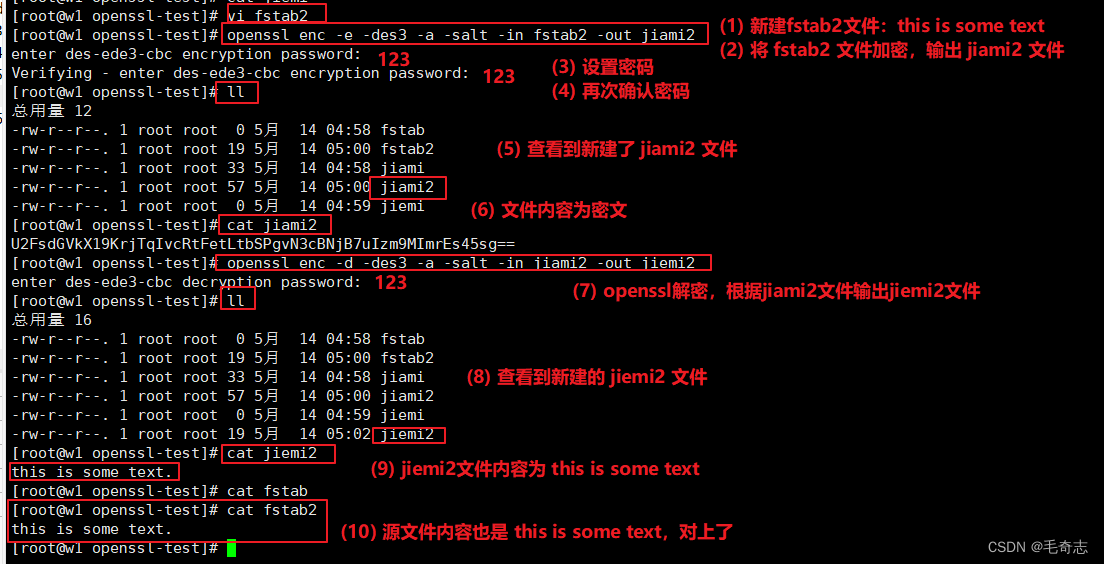
加密：]# openssl enc -e -des3 -a -salt -in fstab -out jiami
解密：]# openssl enc -d -des3 -a -salt -in jiami-out jiemi

openssl实现非对称加密

生成密钥对

首先需要先使用 genrsa 标准命令生成私钥，然后再使用 rsa 标准命令从私钥中提取公钥。

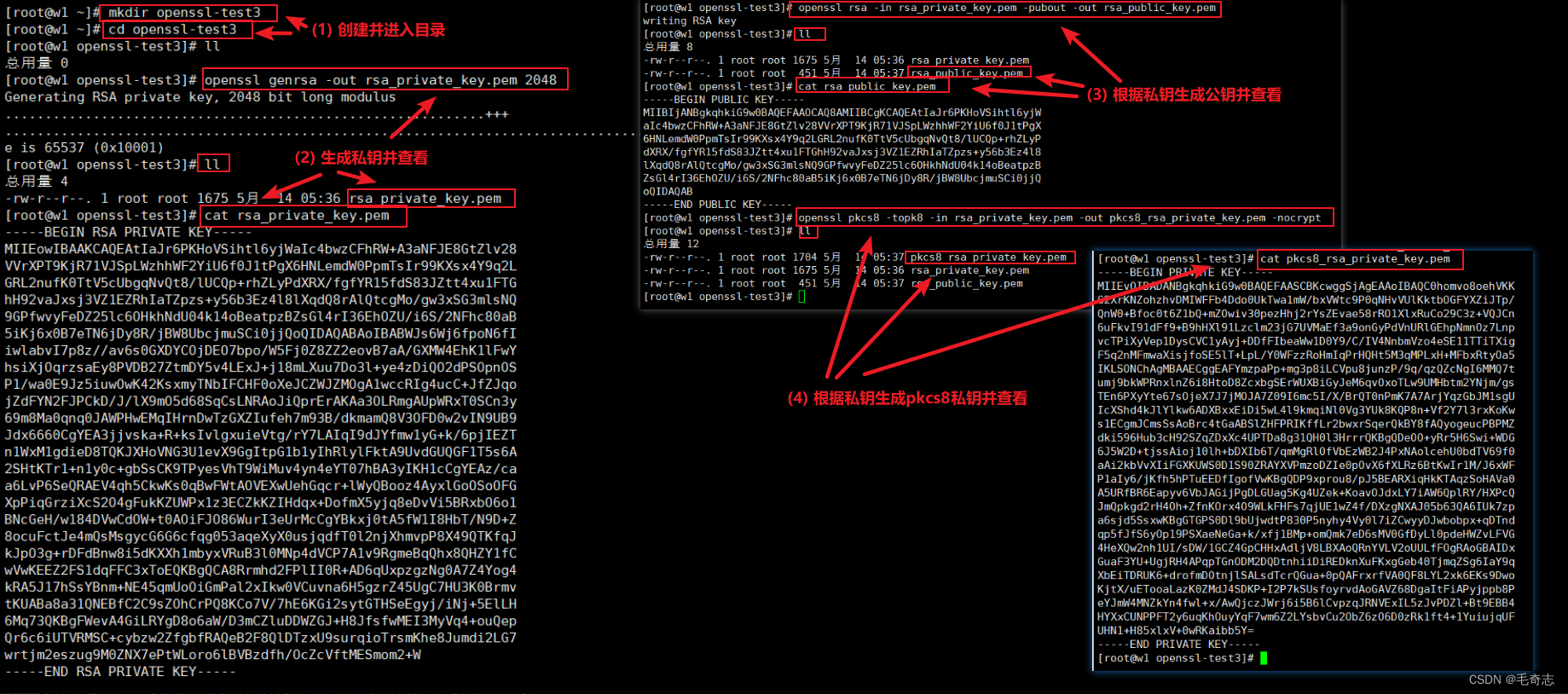
生成密钥对，使用 openssl genrsa / openssl rsa / openssl pkcs8 命令

# openssl genrsa 是命令(生成RSA私钥)，-out rsa_private_key.pem 是输出，2048是加密长度
openssl genrsa -out rsa_private_key.pem 2048
# 也可以执行 openssl genrsa -out rsa_private_key.pem 1024
# openssl rsa 是命令(根据私钥生成公钥)，-pubout 表示首先需要先使用 genrsa 标准命令生成私钥，然后再使用 rsa 标准命令从私钥中提取公钥，-out rsa_public_key.pem 是输出
openssl rsa -in rsa_private_key.pem -pubout -out rsa_public_key.pem
# openssl pkcs8 是命令(对私钥PKCS#8编码)，-in rsa_private_key.pem是输出私钥
# -out pkcs8_rsa_private_key.pem 是输出pkcs8编码的私钥，-nocrypt 表示不采取任何二次加密
openssl pkcs8 -topk8 -in rsa_private_key.pem -out pkcs8_rsa_private_key.pem -nocrypt

生成私钥: openssl genrsa这条命令让openssl随机生成一份私钥，加密长度是1024位。加密长度是指理论上最大允许”被加密的信息“长度的限制，也就是明文的长度限制。随着这个参数的增大（比方说2048），允许的明文长度也会增加，但同时也会造成计算复杂度的极速增长。一般推荐的长度就是2048位。

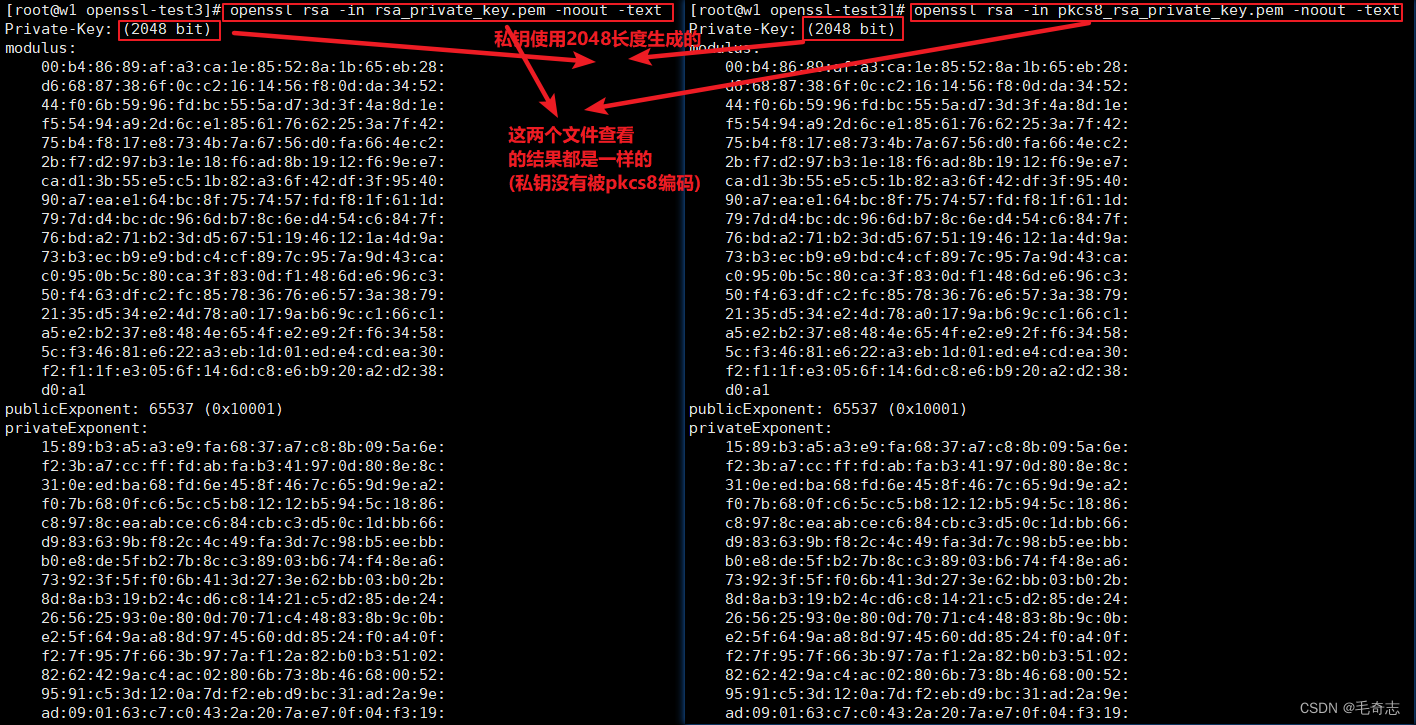
私钥查看，使用 openssl rsa 命令

openssl rsa -in rsa_private_key.pem -noout -text
openssl rsa -in pkcs8_rsa_private_key.pem -noout -text

非对称加密

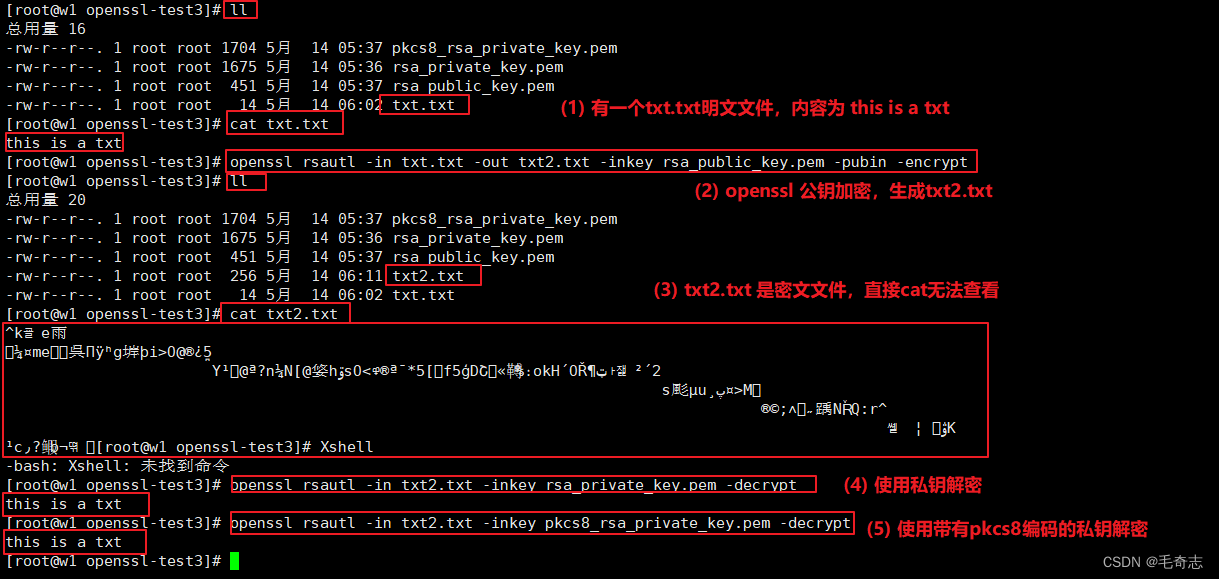
公钥加密，私钥解密，使用 ，使用 openssl rsautl 命令

# 公钥加密
# openssl rsautl 是命令，-in txt.txt 是输入明文，-out txt2.txt 是输出密文
# -inkey rsa_public_key.pem 是密钥， -pubin 说明是这个密钥是公钥
# -encrypt 说明整个命令是加密
openssl rsautl -in txt.txt -out txt2.txt -inkey rsa_public_key.pem -pubin -encrypt

# 私钥解密
# openssl rsautl 是命令，-in txt2.txt 是输入密文
# -inkey pkcs8_rsa_private_key.pem 是密钥，-decrypt 说明整个命令是解密
openssl rsautl -in txt2.txt -inkey rsa_private_key.pem -decrypt
openssl rsautl -in txt2.txt -inkey pkcs8_rsa_private_key.pem -decrypt

数字签名

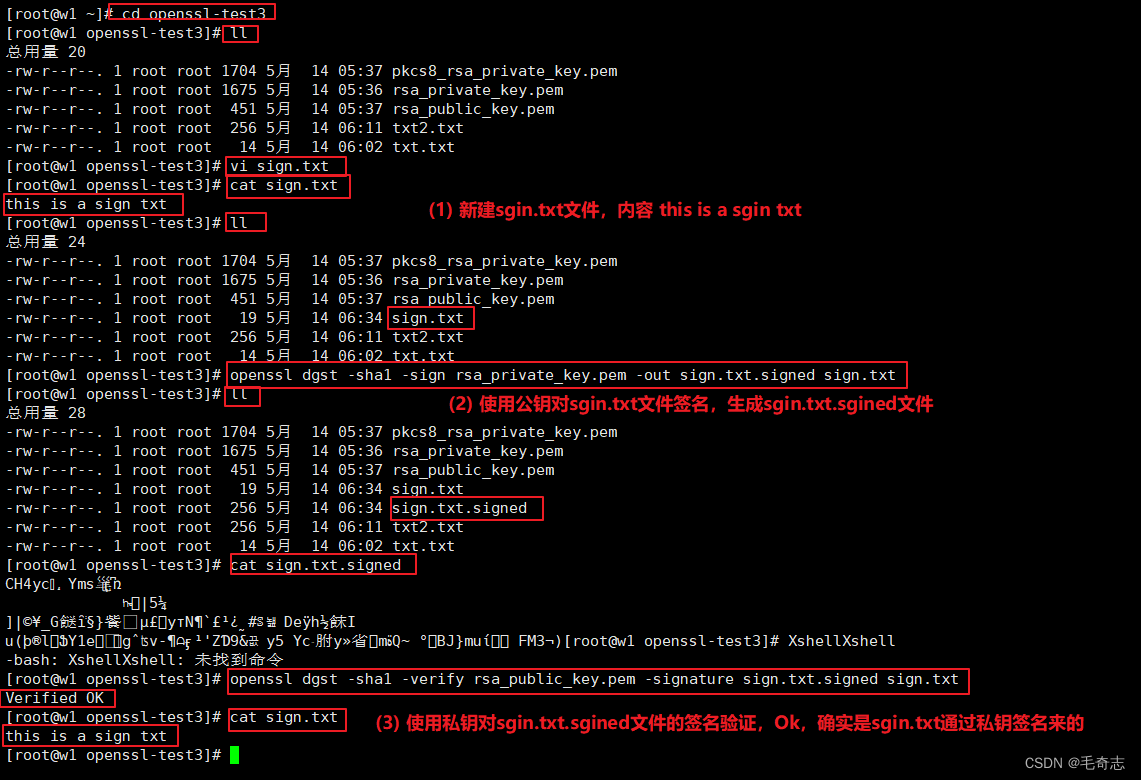
私钥签名，公钥验证，使用 openssl dgst 命令

# 私钥签名
# openssl dgst 是命令，-sha1是签名算法，-sign rsa_private_key.pem 是用于签名的私钥
# -out sign.txt.signed 表示输出的签名文件，sign.txt 表示要签名的文件
openssl dgst -sha1 -sign rsa_private_key.pem -out sign.txt.signed sign.txt
# 公钥验签
# openssl dgst 是命令，-sha1是签名算法，-verify rsa_public_key.pem 是用于验证的公钥
# -signature sign.txt.signed 表示需要被验证的签名文件，sign.txt 表示用来对比的源文件
openssl dgst -sha1 -verify rsa_public_key.pem -signature sign.txt.signed sign.txt

小结

RSA 是非对称加密算法，算法是公开的；公钥加密数据，私钥解密数据；私钥加密数据，公钥解密数据；公钥可以有多个，私钥只要一个。

openssl用来实现非对称加密的常用指令
genrsa 生成一个 RSA 私钥
rsautl 使用 RSA 密钥进行加密、解密、签名和验证等运算
rsa 处理 RSA 密钥的格式转换等问题

非对称加密加密特点
(1) 加密的安全性非常高，加密解密使用不一样的密钥；
(2) 运算的效率非常低，一般只用于加密小数据，或者用于数字签名。

$ openssl rsautl -encrypt -in a.txt -inkey public.pem -pubin -out enc.txt
$ cat enc.txt

1��，~��~Dn�P�Q�

               ]X

��wa�؆���ޅ��T���sJ��z���，l쩨�l��，Y�i�����vD9^Y��)D�:�
RSA 非对称式加解演算法因为先天的限制，无法加密过大的档案，若遇到这个问题时，OpenSSL 会输出如下的错误讯息

Copy
RSA operation error
140736003920840:error:0406D06E:rsa routines:RSA_padding_add_PKCS1_type_2:data too large for key size:/BuildRoot/Library/Caches/com。apple。xbs/Sources/libressl/libressl-22.50。3/libressl/crypto/rsa/rsa_pk1.c:158:

根据CA颁布证书

在linux中与CA相关的信息在/etc/pki目录下，里面有CA，nssdb，rpm-gpg，tls，CA目录就是我们在当前创建CA所要依赖的目录，tls目录是openssL的配置文件存放目录，要在此文件中修改CA的相对路径为绝对路径。

在CA目录中会看到private目录，这个目录是存放CA自己的私钥的

生成ca私钥和ca证书

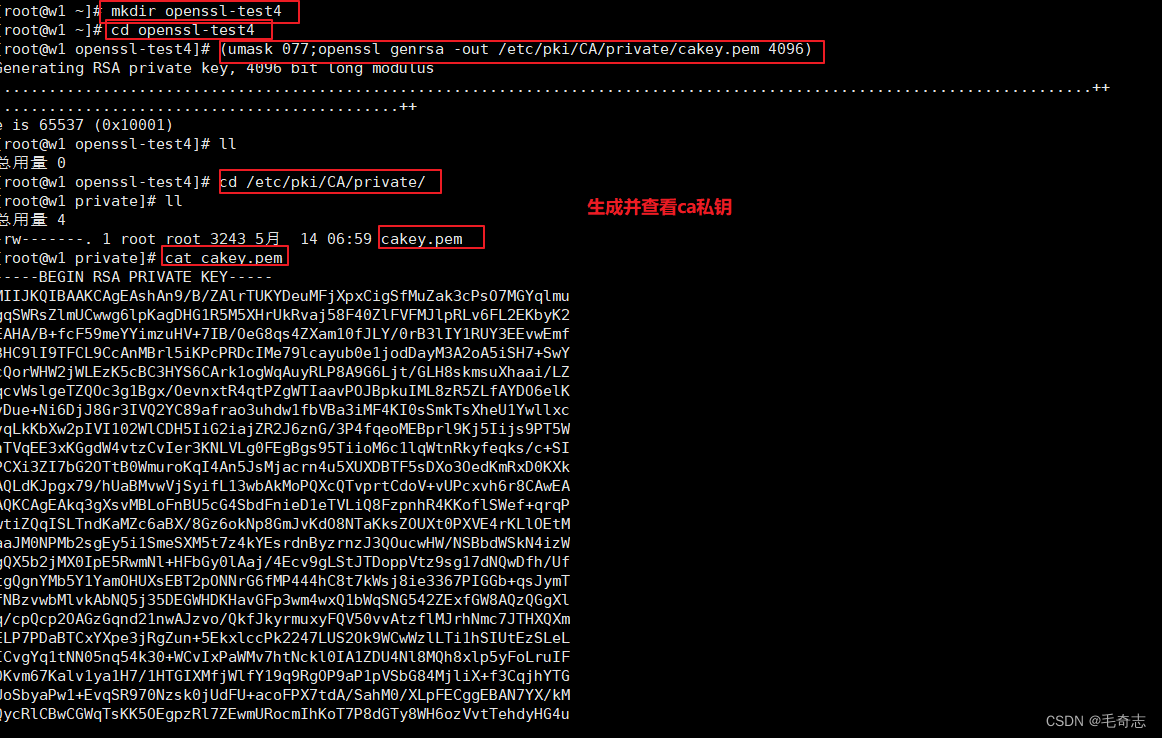
(umask 077;openssl genrsa -out /etc/pki/CA/private/cakey.pem 4096)
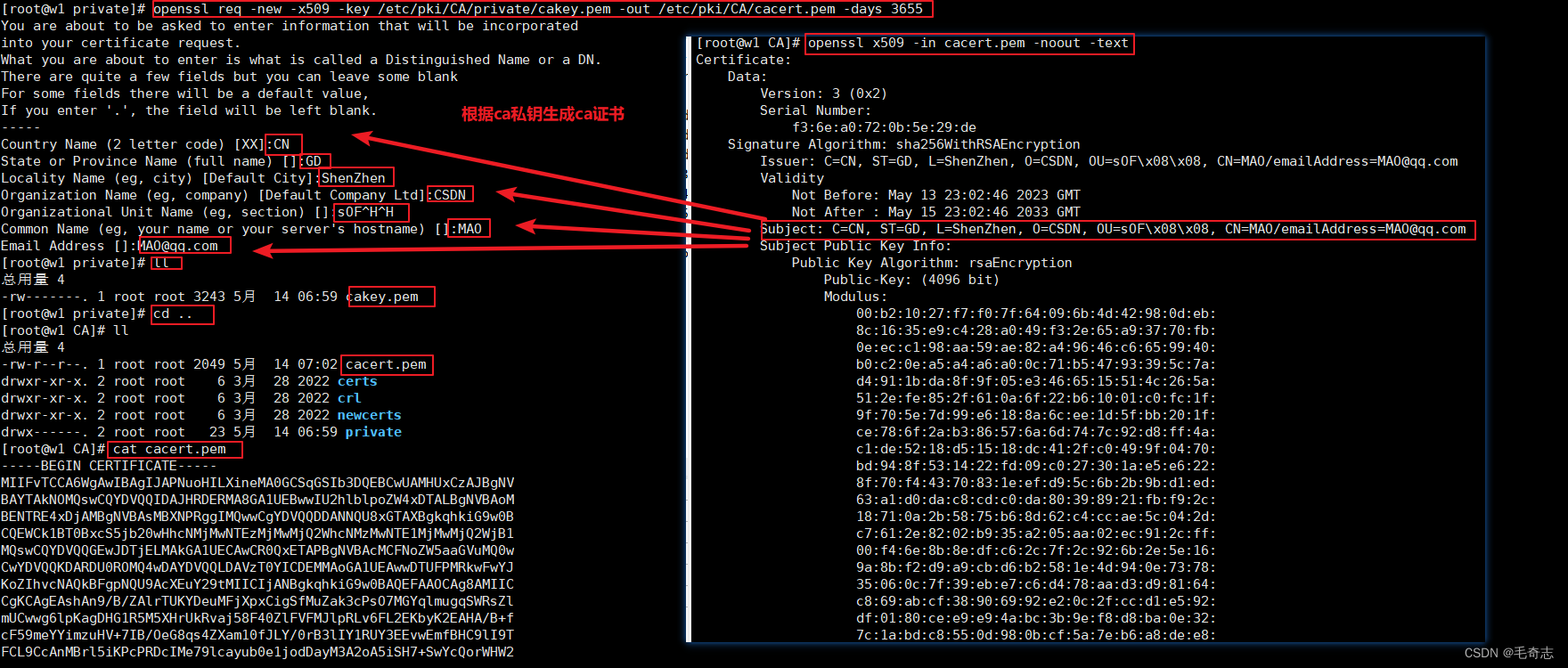
openssl req -new -x509 -key /etc/pki/CA/private/cakey.pem -out /etc/pki/CA/cacert.pem -days 3655
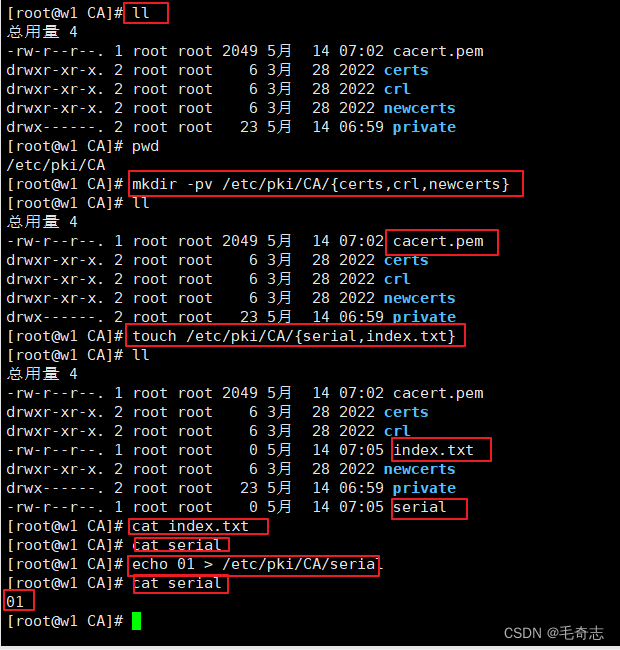
mkdir -pv /etc/pki/CA/{certs,crl,newcerts}
touch /etc/pki/CA/{serial,index.txt}
echo 01 > /etc/pki/CA/serial

根据ca生成证书

要用到证书进行安全通信的服务器，需要向CA请求签署证书

步骤：

1、在用到证书的主机上生成私钥

~]# mkdir /etc/httpd/ssl
~]# cd /etc/httpd/ssl
~]# (umask 077;openssl genrsa -out /etc/httpd/ssl/httpd.key 2048)
blob.png

2、根据私钥 生成 证书签署请求csr

]# openssl req -new -key httpd.key -out httpd.csr -days 365
blob.png

3、将请求csr发送到CA服务器上

]# scp httpd.csr root@10.1.154.97:/etc/pki/CA/certs

4、在CA上,根据证书请求csr,得到crt证书

]#openssl ca -in httpd.csr -out httpd.crt -days 365
blob.png

5、签署证书之后，将证书拷贝给请求的主机

]#scp httpd.crt root@10.1.154.94:/etc/httpd/ssl
blob.png

6、查看证书中的信息

]# openssl x509 -in httpd.crt -noout -text

-serial：查看证书序列号
-subject：查看证书主体信息

7、如何吊销证书，需要在CA上执行

（1）客户端获取要吊销证书的serial

]# openssl x509 -in httpd.crt -noout -serial -subject

（2）CA吊销证书

先根据客户提交的serial和subject信息，对比其与本机数据库index.txt中存储的是否一致，一致，则吊销

]#openssl ca -revoke ./certs/httpd.crt
blob.png

（3）生成证书吊销列表

]#echo 01 > /etc/pki/CA/crlnumber

（4）更新证书吊销列表

]#openssl ca -gencrl -out ./certs/httpd.crt

尾声

OpenSSL 最常用的三个知识点：
第一，对称加密
第二，非对称加密：生成密钥对、公钥加密私钥解密、私钥签名公钥验证
第三，生成CA证书并使用CA证书颁发Server证书

参考文档：OpenSSL 对称加密
生成密钥对
公钥加密，私钥解密
生成密钥对、公钥加密私钥解密、公钥签名私钥验证
生成CA证书、使用CA证书颁发服务端证书
使用CA证书颁发服务端证书