一、堆

1.1堆的特点

1.2如何构造一个最大堆

（1）最大堆的构造以及常用方法的实现

（2）添加操作

（3）删除操作

（3）将任意数组调整为堆

二、TopK问题

2.1使用优先级队列

（1）找最大元素

（2）找最小元素

优先级队列：入队和队列是一样的默认都是队尾入队，出队的时候按照优先级出队，优先级相同的元素按照FIFO出队，优先级高的元素首先出队。

优先级队列的两大特点：

（1）按照优先级出队。

（2）优先级高的元素首先出队。

一、堆

堆是优先级队列背后的数据结构。

我们此处讲得堆其实是二叉堆，基于完全二叉树的二叉堆，广义的堆还有多叉堆（多叉树）。

还有索引堆，普通的对只知道堆顶元素的大小，索引堆可以取得堆中任意位置元素=》在图的最小生成树prim算法和最短路径Diijkstra算法的优化中使用索引堆。

1.1堆的特点

（1）堆首先是完全二叉树，一般使用动态数组（不用存储null结点，元素都靠左排序）存储具体元素。

（2）元素元素的值：

堆中任意一个节点的值<=父节点值（最大堆/大根堆）数据结点>=子树节点。

堆中任意一个节点的值>=父节点值（最小堆/小根堆）数据结点<=子树节点，JDK中的优先级队列默认是最小堆的实现。

在堆中，结点值的大小和节点所处的层次没有明确关系。

关于完全二叉树的节点编号：根据编号以及索引关系，在数据中寻找某一个结点的子节点与父节点编号和索引位置，都从0开始编号，若某个节点的编号（索引）为x。

性质1：判断父节点：

如何判定父结点存在，若存在，索引是多少？parent（x） = （x-1）/2。

当x>0，则一定存在父节点（在二叉树中，只有根节点（根节点索引为0）没有父节点），且父节点的编号为（x-1）/2。

性质2：判断左子树结点

如何判断当前节点x还存在左子树结点？左子树结点编号是多少》

当前完全二叉树的结点个数<=数组最大长度，左子树结点编号为2x+1<size（当前数组种有效的元素个数）。

性质3：判断右子树结点：

右子树结点编号为2x+2<size。

1.2如何构造一个最大堆

（1）最大堆的构造以及常用方法的实现

创建一个线性表的数组，然后创建一个int类型的size来判断存储了多少个数据。

默认状态数组长度为10，也可以通过有参构造自定义数组的长度。

创建三个判断父节点左右节点坐标的方法以及判空方法和输出方法。

public class MaxHeap {
    private List<Integer> arr;
    private int size;
    public MaxHeap() {
        this(10);
    }
    public MaxHeap(int capacity) {
        this.arr = new ArrayList<>(capacity);
    }
    private int parent(int k){
        return (k-1)>>1;
    }
    private int leftChild(int k){
        return (k<<1)+1;
    }
    private int rightChild(int k) {
        return (k << 1) + 2;
    }
    public boolean isEmpty() {
        return size == 0;
    }
    public String toString() {
        return arr.toString();
    }
}

（2）添加操作

尾插方法很简单直接调用线性表的add方法即可，然后size++，在调用我们的siftUp方法。

任意数组都可以看做一颗完全二叉树，因此向堆中插入一个数据，就相当于在数组中插入一个数据（默认尾插）。

siftUp（上浮）不断比较插入后的元素和其父节点的值大小关系，若当前节点值>父节点值，交换他俩元素顺序，直到这个元素落在了正确位置。结束条件：要么此时k==0，已经走到了树根节点，要么此刻arr[k]<=arr[parent[k]]，当前上浮操作结束。

在创建一个swap方法，用来调换两个元素。

    public void add(int val){
        this.arr.add(val);
        size++;
        siftUp(size - 1);
    }
    private void siftUp(int k) {
        while(k>0&&arr.get(k)>arr.get(parent(k))){
            swap(k,parent(k));
            k = parent(k);
        }
    }
    private void swap(int i, int j) {
        int temp = arr.get(i);
        arr.set(i,arr.get(j));
        arr.set(j,temp);
    }

    public static void main(String[] args) {
        MaxHeap heap = new MaxHeap();
        heap.add(17);
        heap.add(11);
        heap.add(3);
        heap.add(2);
        heap.add(5);
        System.out.println(heap);
        heap.add(20);
        System.out.println(heap);
    }

一开始创建好的堆如下。

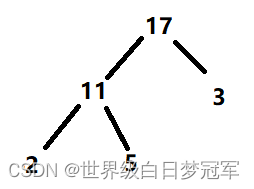
然后要向尾部加入一个元素20。

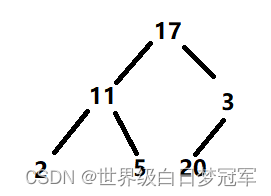
然后调用siftUp方法，先将20与它的父结点值进行比较发现20更大那么就调用swap进行交换。

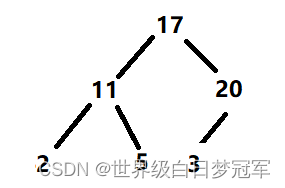
然后继续比较父节点的值，发现还是20更大继续交换。

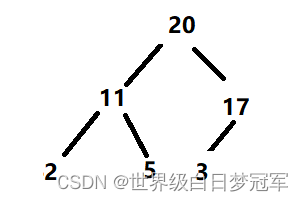
到这时20已经没有父节点了，所以插入操作就结束了。

（3）删除操作

extractMax()：移除当前堆的最大值并返回。

最大堆的最大值在堆顶，删除树根之后，为了对其他子树影响最小，将数组的最后一个元素顶到当前二叉树的堆顶=》这个二叉树仍然是一颗完全二叉树。

需要进行运算的下沉操作siftDown，不断比较当前元素和子节点的最大值的关系，不断交换当前元素和子树的最大值，直到落到正确的位置。也有两个终止条件：1、此时元素已经落到了叶子结点）没有子树了。2、arr[k] >= arr[child[k]]，大于左右子树的最大值，落在最终位置。

实际删除的也是数组的最后一个元素。

peekMax()：查看当前最大堆的最大值元素。

    public int extractMax(){
        if (isEmpty()) {
            throw new NoSuchElementException("heap is empty!cannot extract!");
        }
        int k = arr.get(0);
        arr.set(0,arr.get(size-1));
        arr.remove(size-1);
        size--;
        siftDown(0);
        return k;
    }
    private void siftDown(int k) {
        while (leftChild(k) <size){
            int j = leftChild(k);
            if(j+1<size&&arr.get(j+1)>arr.get(j)){
                j = j+1;
            }
            if(arr.get(k)>=arr.get(j)){
                break;
            }else{
                swap(k,j);
                k = j;
            }
        }
    }

    public static void main(String[] args) {
        MaxHeap heap = new MaxHeap();
        heap.add(3);
        heap.add(2);
        heap.add(5);
        heap.add(17);
        heap.add(11);
        System.out.println(heap);
        heap.add(20);
        System.out.println(heap);
        System.out.println(heap.extractMax());
        System.out.println(heap);
    }

一开始插入操作得到的堆如下：

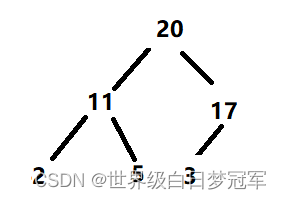
然后删除根节点，将最后一个元素补上。

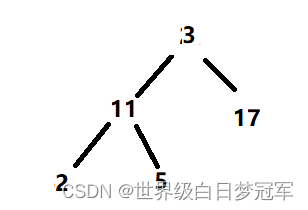
然后比较根节点3的左右子树获取最大值与根节点进行比较，右子树更大并且比根节点还打所以两个位置交换。

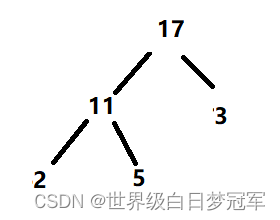
这时3已经是叶子结点不能再继续比较，所以删除操作结束。

（3）将任意数组调整为堆

因为任意数组都可以看做是一棵完全二叉树，将完全二叉树进行适当的调整就可以得到一个堆。

从最后一个非叶子节点开始进行元素的siftDown操作，直到根节点。（最后一个叶子节点的父节点就是最后一个非叶子节点）。

空间复杂度为O（n）。

    public MaxHeap(int[] num){
        this.arr = new ArrayList<>();
        for(int i:num){
            arr.add(i);
            size++;
        }
        for (int i = parent(size-1);i>=0;i--){
            siftDown(i);
        }
    }

    public static void main(String[] args) {
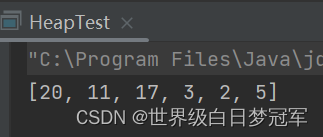
        int[] num = {3,2,17,11,20,5};
        System.out.println(new MaxHeap(num));
    }

二、TopK问题

在一组非常大的数组中，找出前k个最大/最小的元素。

最能想到的方法就是先降序，然后依次取出前50个元素即可。时间复杂度是O（nlogn）。

2.1使用优先级队列

8字口诀：取大用小，取小用大。

这类问题的难点在于如何自定义“大小关系”，巧妙自定义类来定义大小关系，所有的TopK问题都可以使用相同的思路解决。

（1）找最大元素

如果是在100w个数据中心，找出前50个最大的元素。

就建立一个大小为50的最小堆，不断使用最小堆扫描整个数组，扫描完毕之后，最小堆中恰好能保存前50个最大元素。

1、当堆中元素<k，扫描元素直接保存到堆中。

2、当堆中元素个数>=k时，不断比较当前扫描的元素和堆顶元素的情况。

若当前扫描的元素<=堆顶元素，则这个元素小于当前堆中所有元素，直接跳过，一定不是要找的值。若扫描元素>堆顶元素，将堆顶元素移除，将当前元素添加到堆中。

扫描过程中不断地把最小堆的堆顶元素替换为越来越大的值。

3、当整个集合扫描完毕，堆中一定保存了最大的k各元素。

首先用前k各元素创建一个最小堆。

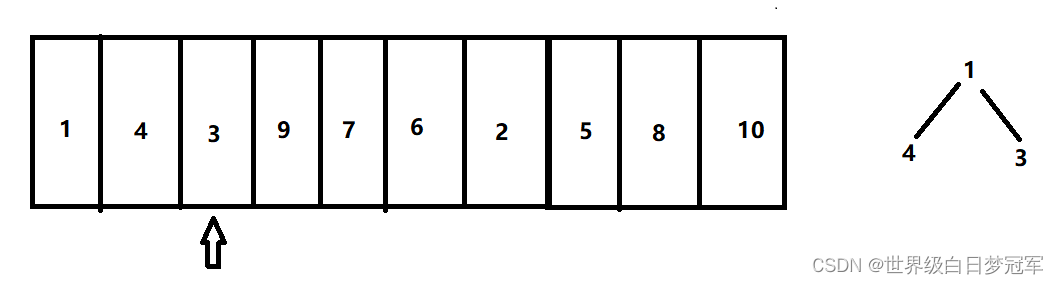
然后走到元素9，比对顶元素大，则出队，然后入队。

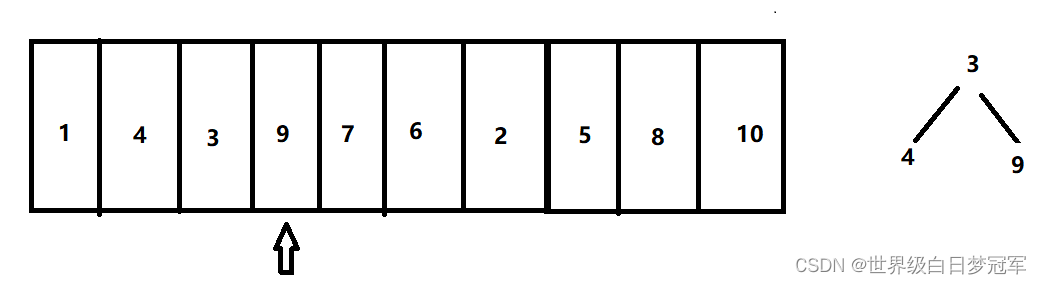
然后走到元素7，比对顶元素大，则出队，然后入队。

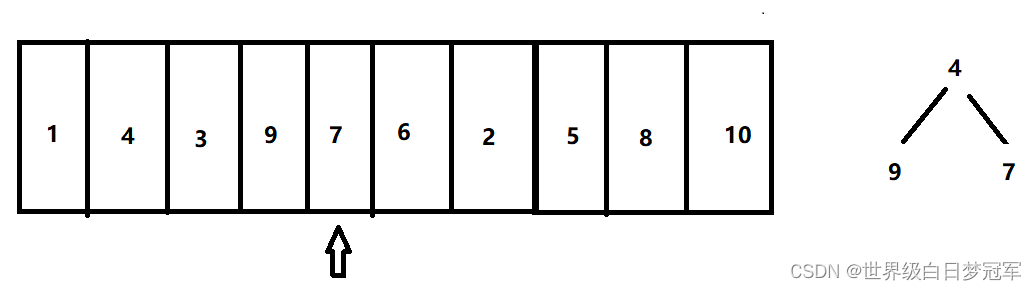
然后走到元素6，比对顶元素大，则出队，然后入队。

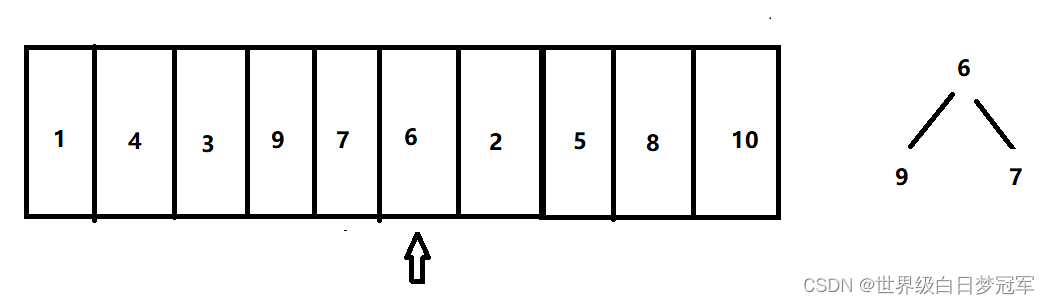
再走到元素2，比堆顶元素小则直接不入队，下一个元素5同理。然后走到元素8，比对顶元素大，则出队，然后入队。

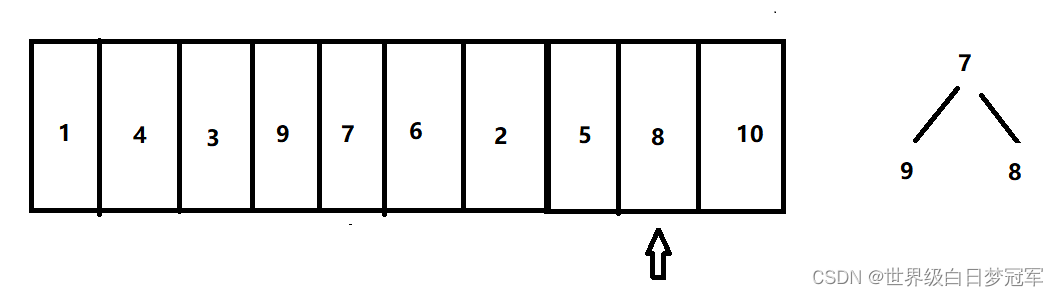
然后最后一个元素10，比对顶元素大，则出队，然后入队。到此优先级队列中的三个元素就是这10个元素里的前3个最大元素。

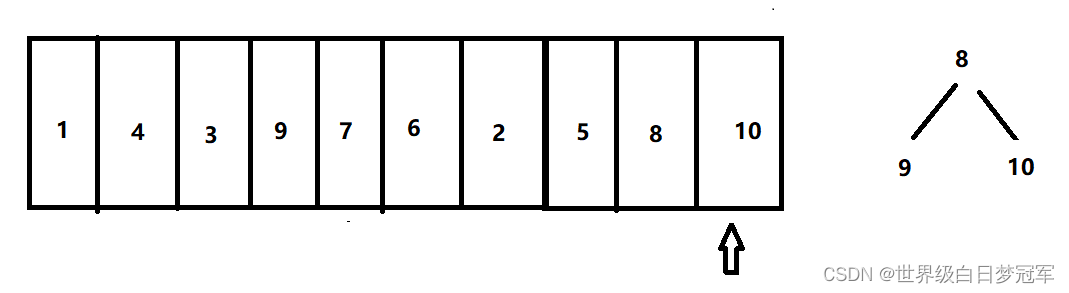
    public static void main(String[] args) {
        int[] arr = {1,4,3,9,7,6,2,5,8,10};
        int k = 3;
        Queue<Integer> queue = new PriorityQueue<>();
        for(int i : arr){
            if(queue.size()<k){
                queue.offer(i);
            }else{
                int top = queue.peek();
                if(i>top){
                    queue.poll();
                    queue.offer(i);
                }
            }
        }
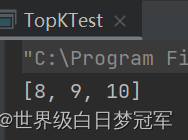
        System.out.println(queue);
    }

第二种解法：直接让所有的元素逐渐入队，如果queue长度超过k，就直接poll，就是移除对顶元素，也是扔出最小的元素，仍然留下k个元素。

    public static void main(String[] args) {
        int[] arr = {1,4,3,9,7,6,2,5,8,10};
        int k = 3;
        Queue<Integer> queue = new PriorityQueue<>();
        for(int i : arr){
            queue.offer(i);
            if(queue.size()>k){
                queue.poll();
            }
        }
        System.out.println(queue);
    }

（2）找最小元素

就需要用到之前讲过的比较器，将JDK中默认的最大堆改为最小堆。

其他的都和最小堆的使用一样。

class IntDesc implements Comparator<Integer>{
    @Override
    public int compare(Integer o1, Integer o2) {
        return o2-o1;
    }
}
public class TopKTest {
    public static void main(String[] args) {
        int[] arr = {1,4,3,9,7,6,2,5,8,10};
        int k = 3;
        Queue<Integer> queue = new PriorityQueue<>(new IntDesc());
        for(int i : arr){
            queue.offer(i);
            if(queue.size()>k){
                queue.poll();
            }
        }
        System.out.println(queue);
    }
}