卡方检验是一种常用的假设检验方法,通常用于分析两个或多个分类变量之间的关系。在医学研究中,卡方检验被广泛应用于分析两种或多种治疗方法的疗效,或者分析某种疾病的发病率与某些危险因素之间的关系。下面我们来看一个卡方检验在医学实例中的应用。
假设我们有一组数据,记录了某种癌症的患病情况和年龄分布。数据如下表所示:
| 年龄段 | 患病人数 | 未患病人数 | 合计 |
|---|---|---|---|
| 20-39 | 35 | 65 | 100 |
| 40-59 | 65 | 135 | 200 |
| 60-79 | 55 | 145 | 200 |
| 80以上 | 45 | 55 | 100 |
| 合计 | 200 | 400 | 600 |
我们的研究假设是,年龄与患癌症的发生率之间存在关系。具体而言,我们想知道,不同年龄段的人群中,患癌症的人数是否与预期相符,还是存在显著差异。
为了回答这个问题,我们需要进行卡方检验。具体步骤如下:
建立假设:我们需要建立一个原假设和一个备择假设。原假设是指不同年龄段的人群中,患癌症的人数符合预期的分布。备择假设是指不同年龄段的人群中,患癌症的人数存在显著差异。
一、基本公式法
实际频数A,理论频数T,Trc=行合计*列合计/总例数。
卡方值=∑((A-T)^2/T),自由度=(R-1)*(C-1)。
1.计算期望值:
例如:100*200/600=33.3333
| 年龄段 | 患病人数期望值 | 未患病人数期望值 |
|---|---|---|
| 20-39 | 33.3333 | 66.6667 |
| 40-59 | 66.6667 | 133.3333 |
| 60-79 | 66.6667 | 133.3333 |
| 80以上 | 33.3333 | 66.6667 |
2.计算卡方值:
卡方值 =∑((A-T)^2/T)= Σ(观察值 – 期望值)^2 / 期望值
例如: (35-33.3333)^2/33.3333=0.0833
| 年龄段 | 患病人数(A-T)^2 /T | 未患病人数(A-T)^2 /T |
|---|---|---|
| 20-39 | 0.0833 | 0.0417 |
| 40-59 | 0.0417 | 0.0208 |
| 60-79 | 2.0417 | 1.0208 |
| 80以上 | 4.0834 | 2.0417 |
卡方值=0.0833+0.0417+0.0417+0.0208+2.0417+1.0208+4.0834+2.0417=9.3751
自由度=(4-1)*(2-1)=3
查卡方临界值表,根据卡方值和自由度可以查找到对应的临界值和p值。在本例中,自由度为3,显著性水平设为0.05。查表可得,卡方临界值为7.81,因为卡方值(9.3751)大于临界值(7.81),所以p值小于显著性水平0.05,所以可以拒绝原假设,接受备择假设,认为不同年龄段的人群中,患癌症的人数存在显著差异。
二、行×列专用公式法
计算公式:
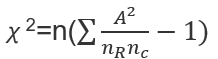
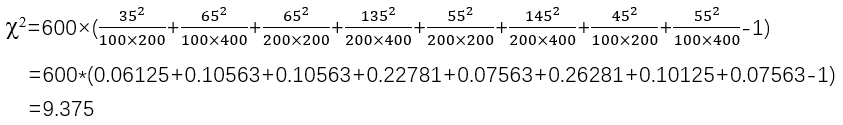
自由度=(4-1)*(2-1)=3
结论同基本公式法。
(卡方检验.医学统计实例详解 - 天兰统计-医学统计助手★卡方检验,t检验,F检验,秩和检验,方差分析)