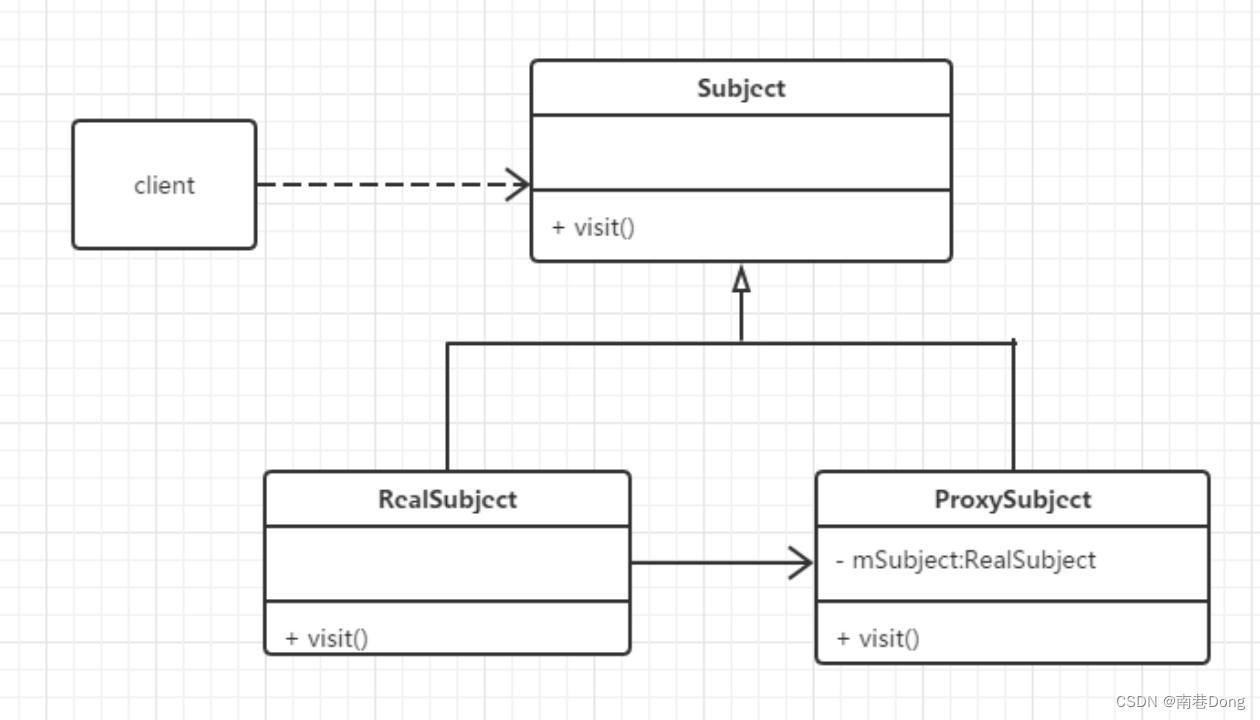
存储系统原理
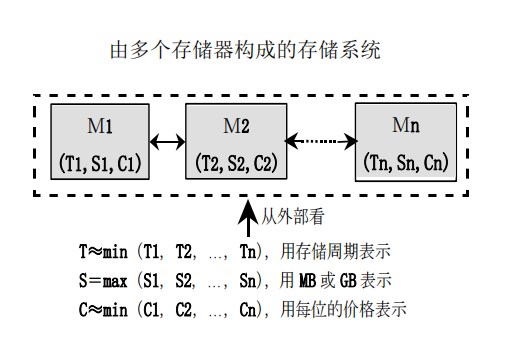
两种典型的存储系统:Cache存储系统和虚拟存储系统。前者主要目的是提高存储器速度,后者有主存储器和硬盘构成,主要用于扩大存储器容量。
存储系统的访问效率
e
=
T
1
T
=
1
H
+
(
1
−
H
)
×
T
2
T
1
=
f
(
H
,
T
2
T
1
)
e=\frac{T_1}{T}=\frac{1}{H+(1-H)\times\frac{T_2}{T_1}}=f(H,\frac{T_2}{T_1})
e=TT1=H+(1−H)×T1T21=f(H,T1T2)
可见访问效率主要与命中率和两级存储器的速度之比有关,访问效率实际上是表示存储系统访问速度能到达系统中访问较快组件的百分之多少。
交叉访问存储器
- 高位交叉访问存储器
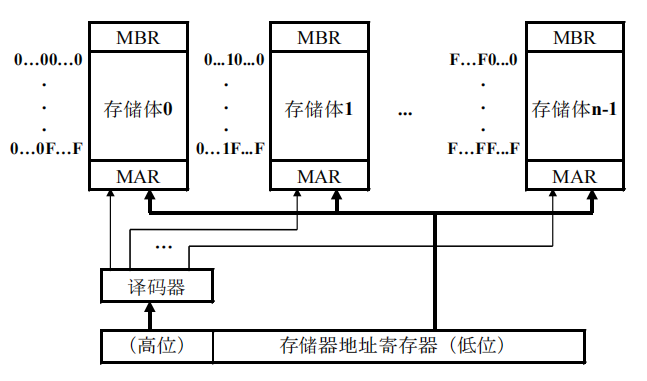
- 低位交叉访问存储器
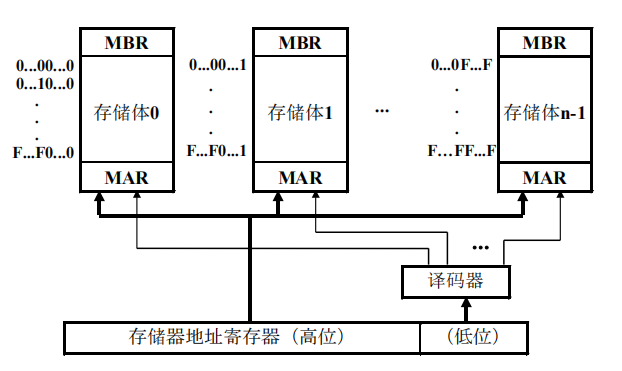
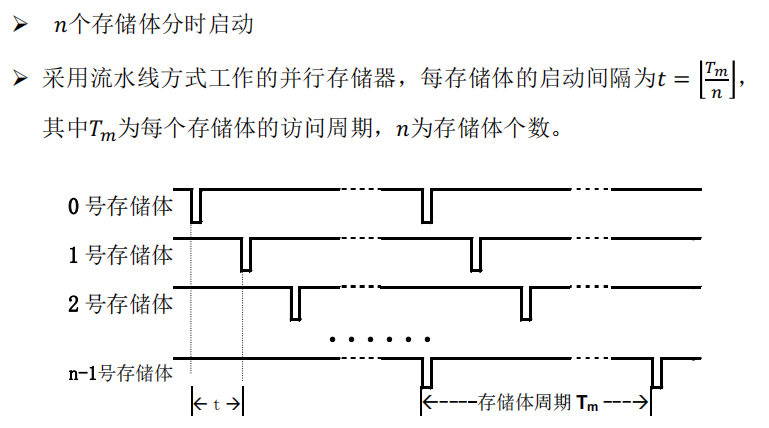
用概率刻画访问冲突问题
共有
n
n
n个存储体,每个存储周期只能取到
k
k
k个有效字,其余
n
−
k
n-k
n−k个存储体有冲突。假设
p
(
k
)
p(k)
p(k)是
k
k
k的概率密度函数PDF,
k
k
k的平均值为:
N
=
∑
k
=
1
n
k
×
p
(
k
)
N=\sum_{k=1}^{n}k\times p(k)
N=k=1∑nk×p(k)
N
N
N是每个存储周期内能够访问到的平均有效字个数,通常称为并行存储器的加速比。
定义转移成功的概率为 g g g,即读出的是转移指令且转移成功的概率。我们有 p ( k ) = ( 1 − g ) k − 1 g , k = 1 , 2 , ⋅ ⋅ ⋅ , n − 1 p(k)=(1-g)^{k-1}g, k=1,2,···,n-1 p(k)=(1−g)k−1g,k=1,2,⋅⋅⋅,n−1,前 ( k − 1 ) (k-1) (k−1)个字不是转移指令或者是不成功的转移指令,第 k k k个字是转移指令且成功转移。
加速比可以通过以下方式计算:
N
=
g
+
2
(
1
−
g
)
g
+
3
(
1
−
g
)
2
g
+
.
.
.
+
(
n
−
1
)
(
1
−
g
)
n
−
2
g
+
n
(
1
−
g
)
n
−
1
N=g+2(1-g)g+3(1-g)^2g+...+(n-1)(1-g)^{n-2}g+n(1-g)^{n-1}
N=g+2(1−g)g+3(1−g)2g+...+(n−1)(1−g)n−2g+n(1−g)n−1
这是一个等差 × \times ×等比数列求和问题(梦回高中)。
首先乘上等比数列的比
(
1
−
q
)
(1-q)
(1−q),得
(
1
−
g
)
N
=
(
1
−
g
)
g
+
2
(
1
−
g
)
2
g
+
3
(
1
−
g
)
3
g
+
.
.
.
+
(
n
−
1
)
(
1
−
g
)
n
−
1
g
+
n
(
1
−
g
)
n
(1-g)N=(1-g)g+2(1-g)^2g+3(1-g)^3g+...+(n-1)(1-g)^{n-1}g+n(1-g)^{n}
(1−g)N=(1−g)g+2(1−g)2g+3(1−g)3g+...+(n−1)(1−g)n−1g+n(1−g)n
和原式作差(注意最后一项形式是不同的(少了
g
g
g)不能相减)得
N
−
(
1
−
g
)
N
=
[
g
+
(
1
−
g
)
g
+
(
1
−
g
)
2
g
+
.
.
.
+
(
1
−
g
)
n
−
2
g
]
+
n
(
1
−
g
)
n
−
1
−
n
(
1
−
g
)
n
−
(
n
−
1
)
(
1
−
g
)
n
−
1
g
N-(1-g)N=[g+(1-g)g+(1-g)^2g+...+(1-g)^{n-2}g]+n(1-g)^{n-1}-n(1-g)^{n}-(n-1)(1-g)^{n-1}g
N−(1−g)N=[g+(1−g)g+(1−g)2g+...+(1−g)n−2g]+n(1−g)n−1−n(1−g)n−(n−1)(1−g)n−1g
前面一部分利用等比数列求和公式
S
n
=
a
1
−
a
n
q
1
−
q
S_n=\frac{a_1-a_nq}{1-q}
Sn=1−qa1−anq,进行求和得到
g
N
=
[
g
−
(
1
−
g
)
n
−
1
g
1
−
(
1
−
g
)
]
+
n
(
1
−
g
)
n
−
1
−
n
(
1
−
g
)
n
−
(
n
−
1
)
(
1
−
g
)
n
−
1
g
gN=[\frac{g-(1-g)^{n-1}g}{1-(1-g)}]+n(1-g)^{n-1}-n(1-g)^{n}-(n-1)(1-g)^{n-1}g
gN=[1−(1−g)g−(1−g)n−1g]+n(1−g)n−1−n(1−g)n−(n−1)(1−g)n−1g
g
N
=
1
−
(
1
−
g
)
n
−
1
+
n
(
1
−
g
)
n
−
1
−
n
(
1
−
g
)
n
−
(
n
−
1
)
(
1
−
g
)
n
−
1
g
gN=1-(1-g)^{n-1}+n(1-g)^{n-1}-n(1-g)^{n}-(n-1)(1-g)^{n-1}g
gN=1−(1−g)n−1+n(1−g)n−1−n(1−g)n−(n−1)(1−g)n−1g
进行合并同类项可得
g
N
=
1
+
(
n
−
1
)
(
1
−
g
)
n
−
1
−
n
(
1
−
g
)
n
−
(
n
−
1
)
(
1
−
g
)
n
−
1
g
gN=1+(n-1)(1-g)^{n-1}-n(1-g)^{n}-(n-1)(1-g)^{n-1}g
gN=1+(n−1)(1−g)n−1−n(1−g)n−(n−1)(1−g)n−1g
g
N
=
1
+
(
n
−
1
)
(
1
−
g
)
n
−
n
(
1
−
g
)
n
gN=1+(n-1)(1-g)^{n}-n(1-g)^{n}
gN=1+(n−1)(1−g)n−n(1−g)n
g
N
=
1
−
(
1
−
g
)
n
gN=1-(1-g)^{n}
gN=1−(1−g)n
最终得到
N
=
1
−
(
1
−
g
)
n
g
N=\frac{1-(1-g)^{n}}{g}
N=g1−(1−g)n
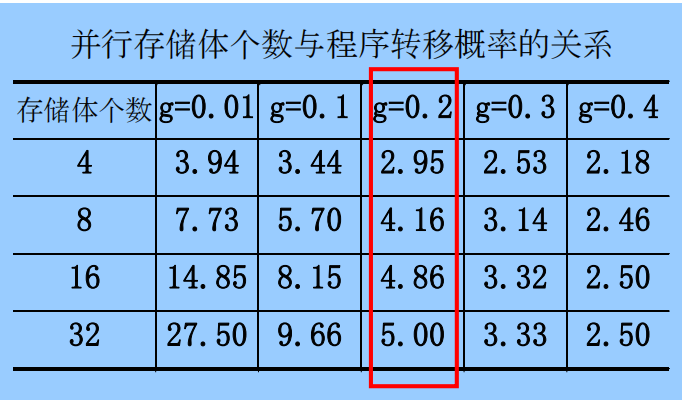
通过打表查看,加速比和存储体个数以及程序转移概率之间的关系,由于转移指令的存在,实际的加速比大受限制。
虚拟存储器
多级页表

保证最后一级页表可以容纳所有虚实页号之间的映射:
2
g
×
N
p
N
d
≥
N
v
N
p
2^g\times\frac{N_p}{N_d}\geq\frac{N_v}{N_p}
2g×NdNp≥NpNv
取对数得
g
(
l
o
g
2
N
p
−
l
o
g
2
N
d
)
≥
(
l
o
g
2
N
v
−
l
o
g
2
N
p
)
g(log_2N_p-log_2N_d)\geq(log_2N_v-log_2N_p)
g(log2Np−log2Nd)≥(log2Nv−log2Np)
最小满足以上条件的
g
g
g为
l
o
g
2
N
v
−
l
o
g
2
N
p
l
o
g
2
N
p
−
l
o
g
2
N
d
\frac{log_2N_v-log_2N_p}{log_2N_p-log_2N_d}
log2Np−log2Ndlog2Nv−log2Np。
快慢表

- 快表按内容相联访问,内容:用户号+虚页号+实页号
- 慢表按地址,将用户号和虚页号视为地址,内容:1位装入位+实页号
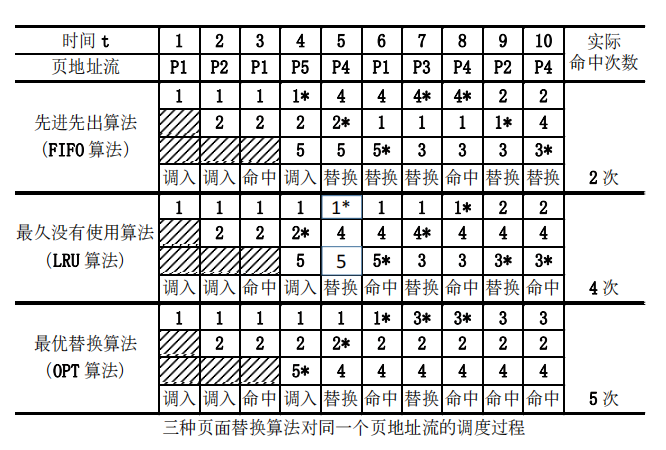
页面替换算法



高速缓冲存储器
todo