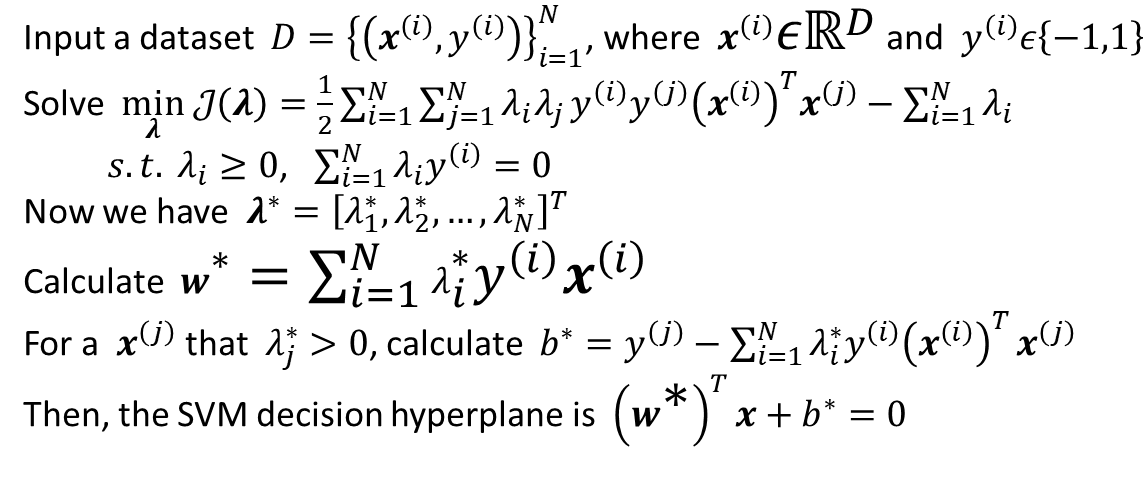经典动态规划：最长递增子序列

news2025/4/8 20:09:53

力扣第300题：[最长递增子序列]，这道题是非常经典的动态规划和二分查找的题目，我们先看dp:

第一种解法：动态规划

我们先看题目的示例1：

输入：nums = [10,9,2,5,3,7,101,18]
输出：4
解释：最长递增子序列是 [2,3,7,101]，因此长度为 4 。

我们写这个题前，先理解一下题目的意思，题目中说的[最长递增子序列]是什么意思，结合案例我们知道，可以是不连续的，只要大就算。
我们观察一下示例1，最长递增子序列是[2,3,7,101],那我们从下标为0的数开始观察，看看有什么规律，为了方便，我们定义一个数组arr来记录一下最长递增子序列的长度，数组的长度自然为nums数组的长度。那么arr[i]就表示以nums[i]这个数结尾的最长递增子序列的长度。
观察示例1我们不难发现，arr应该长这样：

nums = [10,9,2,5,3...
arr  = [1,1,1,2,2...

因为10本身是一个，所以是1，9呢又比10小，所以也是1，2比前面的都小，所以也是1,那么5呢？5前面有个比他小的2，加上本身，所以是不是就是2了？同理，arr[4]也是2。
我们推举出来了arr[0..4]的结果，那么后面的应该是什么呢？
我们学过数学归纳法，我们先假设这个结论在 i < n 时成立，然后根据这个假设，想办法推导证明出 i = n 的时候此结论也成立，那么按照前面的规律来说，我们想找到i=n时的结论，是不是就要找到前i-1个比nums[i]小的数，然后统计有几个这样的数，arr[i]是不是就等于多少？ 换句话说，是不是只要找到了比nums[i]小的数，假如下标为j，那么

arr[i] = arr[j] + 1

事实证明，就是这样的，所以arr[5]=arr[4] + 1 = 3，arr[6]=arr[5] + 1 = 4。但是这是没有重复的前提下，那如果有重复呢？此时就要改成

 arr[i] = Math.max(arr[i],arr[j] + 1);

那么这个数组arr更像什么？没错就是我们熟悉的dp,所以将数组更名为dp
那么我们的思路是不是就是

for (int i = 0; i < nums.length; i++) {
    for (int j = 0; j < i; j++) {
        // 寻找 nums[0..j-1] 中比 nums[i] 小的元素
        if (nums[i] > nums[j]) {
            // 把 nums[i] 接在后面，即可形成长度为 dp[j] + 1，
            // 且以 nums[i] 为结尾的递增子序列
            dp[i] = Math.max(dp[i], dp[j] + 1);
        }
    }
}

我们还需要找到一个满足条件的最大值：

int res = 0;
for (int i = 0; i < nums.length; i++) {
    for....
    res = Math.max(res,dp[i]);
}

所以完整的代码如下：

 public int lengthOfLIS(int[] nums) {
       int[] dp = new int[nums.length];
        int res = 0;
        Arrays.fill(dp,1);
        for(int i =0;i<nums.length;i++){
            for(int j = 0;j<i;j++){
                if(nums[i] > nums[j]){
                    dp[i] = Math.max(dp[i],dp[j] + 1);
                }
            }
            res = Math.max(res,dp[i]);
        }
        return res;
    }

🔴第二种解法：二分查找

相信大家都玩过Windows的经典游戏—[ 蜘蛛纸牌 ]
游戏大致玩法就是，将小的牌放到大牌下面，先收集玩A-K的即为胜利
有一种叫做patience game的纸牌玩法和他类似：
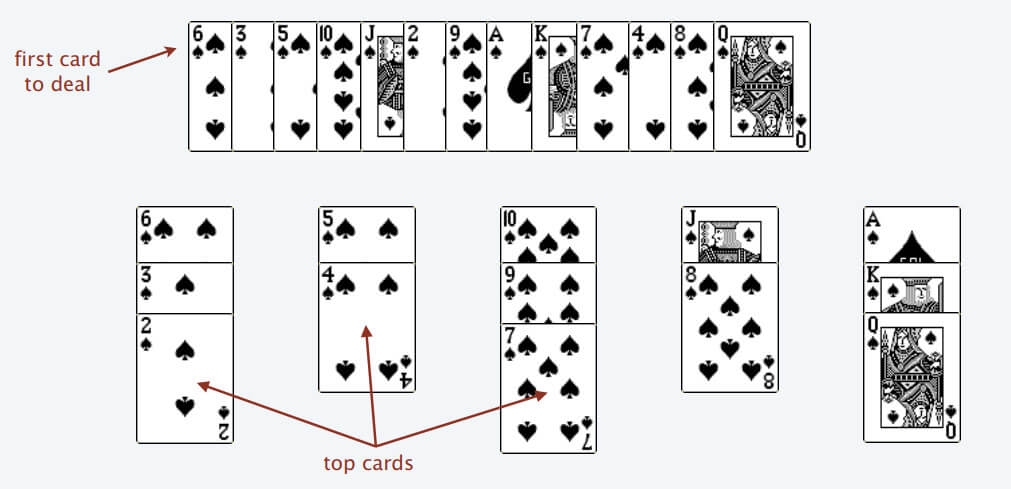
首先，给你一排扑克牌，我们像遍历数组那样从左到右一张一张处理这些扑克牌，最终要把这些牌分成若干堆。

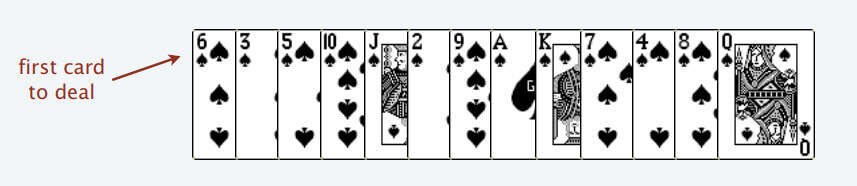
处理这些扑克牌要遵循以下规则：
只能把点数小的牌压到点数比它大的牌上；如果当前牌点数较大没有可以放置的堆，则新建一个堆，把这张牌放进去；如果当前牌有多个堆可供选择，则选择最左边的那一堆放置。

比如说上述的扑克牌最终会被分成这样 5 堆（我们认为纸牌 A 的牌面是最大的，纸牌 2 的牌面是最小的）。

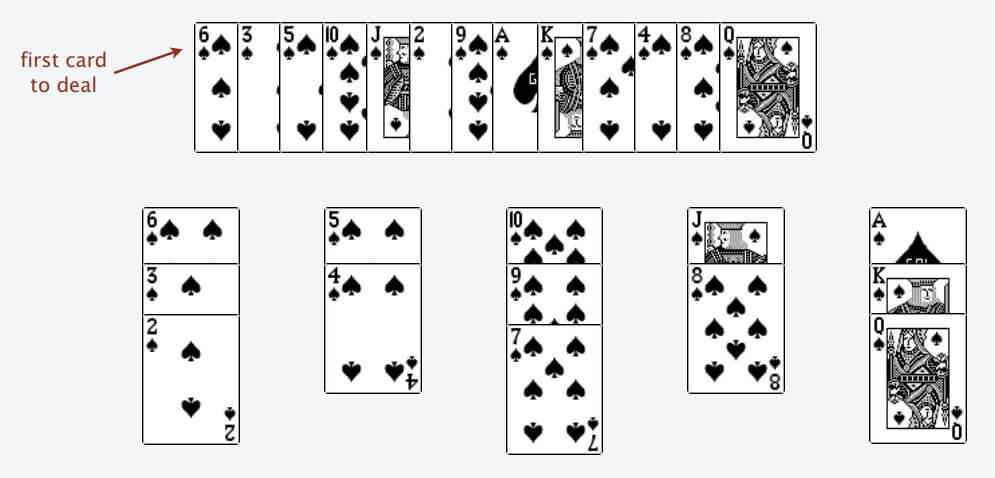
为什么遇到多个可选择堆的时候要放到最左边的堆上呢？因为这样可以保证牌堆顶的牌有序（2, 4, 7, 8, Q），证明略。

按照上述规则执行，可以算出最长递增子序列，牌的堆数就是最长递增子序列的长度，证明略。

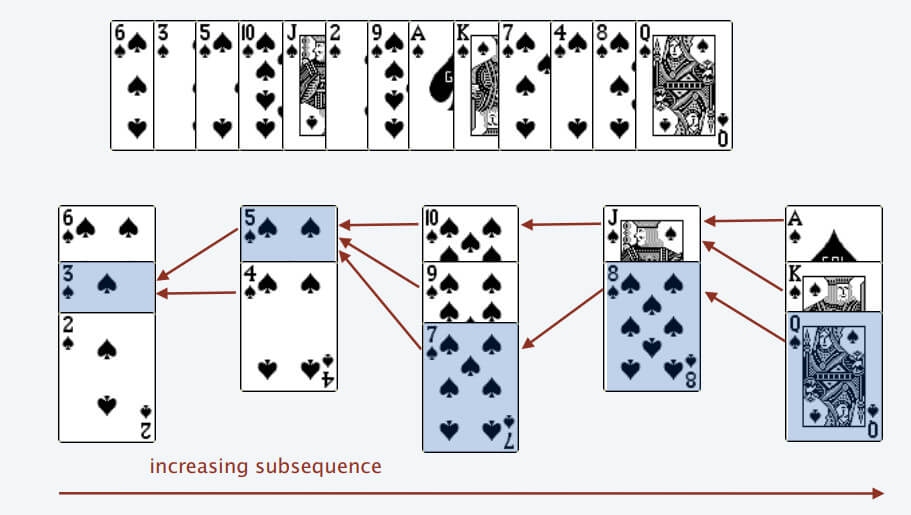
我们只要把处理扑克牌的过程编程写出来即可。每次处理一张扑克牌不是要找一个合适的牌堆顶来放吗，牌堆顶的牌不是有序吗，这就能用到二分查找了：用二分查找来搜索当前牌应放置的位置。

public int lengthOfLIS(int[] nums) {
	//顶部牌
       int[] top = new int[nums.length];
	//初始化牌堆为0
       int piles = 0;
       for(int i = 0;i<nums.length;i++){
	//当前需要排序的牌
           int poker = nums[i];
		//right为牌堆界
           int left = 0,right = piles;
	//此二分查找的目的不在于找到这个值，
	//目的在于找到left和right不断缩小过程中的非常趋近的区间k，
	//当left=right时跳出循环
           while(left < right){
               int mid = (left + right)/2;
               if(top[mid] >= nums[i]){
                   right = mid;
               }else{
                   left = mid +1;
               }
           }
	//如果k为边界（因为约定好只有有满足的，
        //优先选择左边第一个满足的，如果不满足到边界了，说明没有了）
	//没有找到合适的边界，新建一堆
           if(left == piles) piles++;
	   //覆盖顶部的值，因为每次找满足之后都会放到第一个，下面的值无所谓了
           top[left] = poker;
       }
	//堆的数量就是最长递增子序列的数量
       return piles;
    }