回归分析-简单线性回归模型

在大数据分析中，回归分析是一种预测性的建模技术，它研究的是因变量（目标）和自变量（预测器）之间的关系。这种技术通常用于预测分析，时间序列模型以及发现变量之间的因果关系。例如，司机的鲁莽驾驶与道路交通事故数量之间的关系，最好的研究方法就是回归。来自百度百科
可以说是数据分析中非常简单的一个知识点，有一点点统计、分析、建模经验的人都知道这个分析的含义，也会用各种工具来做这个分析。这里面想把这个分析背后的细节讲讲清楚，也就是后面的数学原理。

一元线性回归是最简单的形式，它只包含一个自变量和一个因变量，二者直接的关系可以用一条直线近似表示，这种回归分析被称为简单线性回归。

可以用下面的公式表示 y是因变量，x是自变量。
$$\overline{y}=ax+b\text{\hspace{1em}(1.1)}$$

假如广告投入与销售额存在这样一种线性关系，收集了一组广告投入与销售额的历史数据，那么如何确定a和b的值呢？这里先给出答案，后面再说推导过程。

$$b=\overline{y}-a\overline{x}\text{\hspace{1em}(1.2)}$$
$$a=\frac{{\sum }_{i=1}^n(x_i-\overline{x})(y_i-\overline{y})}{{\sum }_{i=1}^n(x_i-\overline{x}{)}^2}\text{\hspace{1em}(1.3)}$$

通过例子验算

摘自《商务与经济统计》这本书的一个示例

Armand比萨饼连锁店是经营意大利食品的餐馆，它们分布在美国5个州的范围内。Armand比萨饼连锁店的最佳位置在大学校园附近。管理人员确信，这些连锁店的季度销售收入(用y表示)与学生人数(用x表示)是正相关的。也就是说，学生较多比学生较少的校园附近的连锁店有获得较大的季度销售收入的倾向。利用回归分析，我们能求出一个说明因变量y是如何依赖自变量x的方程。

下面是10家Armand比萨饼店的季度销售数据，观测次数n=10，数据中给出了应变量为比萨饼店季度销售额，自变量为当前比萨饼店所在的学校的学生人数，现有一家新开的比萨饼店，已知这家店附近的学生人数，求比萨饼店季度销售额。

数据如下表

序号	$x_i$	$y_i$	$x_i-\overline{x}$	$y_i-\overline{y}$	$(x_i-\overline{x}{)}^2$	$(x_i-\overline{x})(y_i-\overline{y})$
1	2	58	-12	-72	144	864
2	6	105	-8	-25	64	200
3	8	88	-6	-42	36	252
4	8	118	-6	-12	36	72
5	12	117	-2	-13	4	26
6	16	137	2	7	4	14
7	20	157	6	27	36	162
8	20	169	6	39	36	234
9	22	149	8	19	64	152
10	26	202	12	72	144	864

根据上表计算
$\overline{x}=14$ ；$\overline{y}=130$ ；${\sum }_{i=1}^n(x_i-\overline{x}{)}^2=568$ ；${\sum }_{i=1}^n(x_i-\overline{x})(y_i-\overline{y})=2840$

求解简单线性回归方程

按公式 1.3 计算系统 a
$$a=\frac{{\sum }_{i=1}^n(x_i-\overline{x})(y_i-\overline{y})}{{\sum }_{i=1}^n(x_i-\overline{x}{)}^2}=5$$
按公式1.2 计算系数 b
$$b=\overline{y}-a\overline{x}=60$$
解得方程为
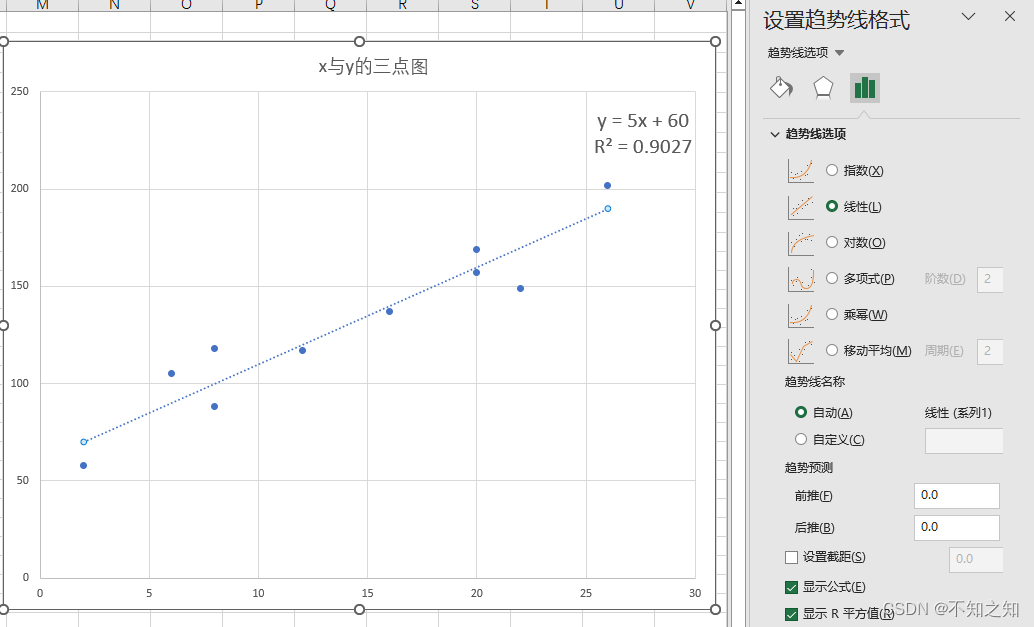
$$\overline{y}=5x+60$$

与用Excel生成散点图，添加趋势线，显示的线性方程一致。

推导过程

因为本人基本忘光了高中和大学的数学知识，所以在学习原理的过程中废了很多时间，这个推导过程适合和我一样数学底子弱的人，大神可以略过！！

---

言归正传，上述方程（1.1）叫做Y对x的回归直线方程，b叫做回归系数。要想确定回归直线方程，我们只需确定a与回归系数b即可。

该方程预测出来的y值和实际的值差别越小越好，只有如此才能使直线最贴近已知点。我们求回归直线方程的过程其实就是求差别最小值的过程。

一个很自然的想法是把各个差加起来作为总差。可是，由于差有正有负，直接相加会互相抵消， 一般做法是我们用差的平方和，即：

$$Q=\sum _{i=1}^n(y_i-\widehat{y_i}{)}^2=\sum _{i=1}^n(y_i-(a{x}_i+b){)}^2=\sum _{i=1}^n(y_i-a{x}_i-b{)}^2\text{\hspace{1em}(2.1)}$$

Q作为总差 ，并使之达到最小。这样回归直线就是所有直线中Q取最小值的那一条。由于平方又叫二乘方，所以这种使“离差平方和为最小”的方法，叫做最小二乘法。

---

怎么求最小的Q值呢？这是一个二次函数，对其求导，导数为0的时候取得最小值。至于为什么导数为了取值最小可以参考这篇文章极值与导数。这里就引出了导数，对导数不明白的可以参考这篇文章导数概念。

由于公式2.1描述的是因变量Q关于自变量a,b的函数 $Q=f(a,b) $ 是个二元函数，对二元函数求导，可以让其中一个自变量b固定（即看作常量），这时它就是a的一元函数，这时函数对a求导，就称为二元函数Q对于a的偏导数，又引入了偏导数的概念，不明白偏导数的可以参考这篇文章偏导数。

求导过程

$$\frac{\partial f}{\partial b}=2\sum _{i=1}^n(y_i-a{x}_i-b))\text{\hspace{1em}(2.2)}$$

2.2 式的推导过程
①幂函数求导公式
若$f(x)=x^n$，则$f\prime (x)=n\cdot x^{n-1}$
②复合函数求导法则
$ f(g(x)) $ 求导
令 $u=g(x)$ ，$[f(g(x))]\prime =f\prime (u)g\prime (x)$
③ 根据上两条规程推导
令 $u=y_i-ax_i-b $
$\frac{\partial f}{\partial b}=\sum_{i=1}^n{2u} \cdot (-1)=-2\sum_{i=1}^n(y_i-ax_i-b) $

$$\frac{\partial f}{\partial a}=\sum _{i=1}^{n}2(y_i-a{x}_i-b)\cdot (-x_i)=-2(\sum _{i=1}^n{x}_i{y}_i-a\sum _{i=1}^n{x}_i^2-b\sum _{i=1}^n{x}_i)\text{\hspace{1em}(2.3)}$$

令 $\frac{\partial f}{\partial a}=0$，$\frac{\partial f}{\partial b}=0$， $n\overline{x}={\sum }_{i=1}^n{x}_i$ ， $n\overline{y}={\sum }_{i=1}^n{y}_i$
求解 a 和 b
$$n\overline{y}-an\overline{x}-nb=0\text{\hspace{1em}(2.4)}$$
$$\sum _{i=1}^n{x}_i{y}_i-a\sum _{i=1}^n{x}_i^2-b\sum _{i=1}^n{x}_i=0\text{\hspace{1em}(2.5)}$$
$$b=\overline{y}-a\overline{x}\text{\hspace{1em}(2.6)}$$
$$\sum _{i=1}^n{x}_i{y}_i-a\sum _{i=1}^n{x}_i^2-\overline{y}\sum _{i=1}^n{x}_i+a\overline{x}\sum _{i=1}^n{x}_i=0\text{\hspace{1em}(2.7)}$$

$$a=\frac{{\sum }_{i=0}^n{x}_i{y}_i-\overline{y}{\sum }_{i=0}^n{x}_i}{{\sum }_{i=0}^n{x}_i^2-\overline{x}{\sum }_{i=0}^n{x}_i}=\frac{{\sum }_{i=0}^n(x_i-\overline{x})(y_i-\overline{y})}{{\sum }_{i=0}^n(x_i-\overline{x}{)}^2}\text{\hspace{1em}(2.8)}$$

式2.8 的推导请看求和性质

求和性质

求和性质，具体可以参考Introductory Econometrics A Modern Approach (Fourth Edition) 一书（计量经济学导论，第4版，杰弗里·M·伍德里奇 著）的附录A。

求和性质证明

$$\begin{array}{rl}& \sum _{i=0}^n(x_i-\overline{x}{)}^2=\sum _{i=0}^n(x_i^2-2x_i\overline{x}+{\overline{x}}^2)\\ & =\sum _{i=0}^n{x}_i^2-2\overline{x}\sum _{i=0}^n{x}_i+\sum _{i=0}^n{\overline{x}}^2\\ & =\sum _{i=0}^n{x}_i^2-2n{\overline{x}}^2+n{\overline{x}}^2\\ & =\sum _{i=0}^n{x}_i^2-n{\overline{x}}^2\\ & =\sum _{i=0}^n{x}_i^2-\overline{x}\sum _{i=0}^n{x}_i\end{array}$$

分母得证

$$\begin{array}{rl}& \sum _{i=0}^n(x_i-\overline{x})(y_i-\overline{y})\\ & =\sum _{i=0}^n(x_i{y}_i-x_i\overline{y}-\overline{x}{y}_i+\overline{x}\overline{y})\\ & =\sum _{i=0}^n{x}_i{y}_i-n\overline{x}\overline{y}-n\overline{x}\overline{y}+n\overline{x}\overline{y}\\ & =\sum _{i=0}^n{x}_i{y}_i-\overline{y}\sum _{i=0}^n{x}_i\end{array}$$

分子得证

很原始（笨）的导数推导过程

求函数f(x,y),对x的偏导

$$\frac{\partial f}{\partial x}=\underset{\Delta x\to 0}{\lim }\frac{f(x+\Delta x,y)-f(x,y)}{\Delta x}\text{\hspace{1em}(3.1)}$$

求函数f(x,y),对y的偏导

$$\frac{\partial f}{\partial y}=\underset{\Delta y\to 0}{\lim }\frac{f(x,y+\Delta y)-f(x,y)}{\Delta y}\text{\hspace{1em}(3.2)}$$

对 a 求偏导

$$\frac{\partial f}{\partial a}=\underset{\Delta a\to 0}{\lim }\sum _{i=1}^n\frac{(yi-((a+\Delta a)x_i+b){)}^2-(y_i-(a{x}_i+b){)}^2}{\Delta a}\text{\hspace{1em}(3.3)}$$

$$\frac{\partial f}{\partial a}=\underset{\Delta a\to 0}{\lim }\sum _{i=1}^n\frac{((yi-b)-(a+\Delta a)x_i{)}^2-((y_i-b)-a{x}_i{)}^2}{\Delta a}\text{\hspace{1em}(3.4)}$$

$$\frac{\partial f}{\partial a}=\underset{\Delta a\to 0}{\lim }\sum _{i=1}^n\frac{((yi-b{)}^2-2x_i(yi-b)(a+\Delta a)+x_i^2(a+\Delta a{)}^2)-((y_i-b{)}^2-2a(y_i-b)x_i+a^2{x}_i^2)}{\Delta a}\text{\hspace{1em}(3.5)}$$

$$\frac{\partial f}{\partial a}=\underset{\Delta a\to 0}{\lim }\sum _{i=1}^n\frac{(yi-b{)}^2-2x_i(y_i-b)(a+\Delta a)+x_i^2(a+\Delta a{)}^2-(y_i-b{)}^2+2a(y_i-b)x_i-a^2{x}_i^2}{\Delta a}\text{\hspace{1em}(3.6)}$$

$$\frac{\partial f}{\partial a}=\underset{\Delta a\to 0}{\lim }\sum _{i=1}^n\frac{-2x_i(a+\Delta a)(y_i-b)+x_i^2(a+\Delta a{)}^2+2a(y_i-b)x_i-a^2{x}_i^2}{\Delta a}\text{\hspace{1em}(3.7)}$$

$$\frac{\partial f}{\partial a}=\underset{\Delta a\to 0}{\lim }\sum _{i=1}^n\frac{-2x_i(y_i-b)\Delta a+x_i^2(a+\Delta a{)}^2-a^2{x}_i^2}{\Delta a}\text{\hspace{1em}(3.8)}$$

$$\frac{\partial f}{\partial a}=\underset{\Delta a\to 0}{\lim }\sum _{i=1}^n\frac{-2x_i(y_i-b)\Delta a+x_i^2(a^2+2a\Delta a+\Delta a^2)-a^2{x}_i^2}{\Delta a}\text{\hspace{1em}(3.9)}$$

$$\frac{\partial f}{\partial a}=\underset{\Delta a\to 0}{\lim }\sum _{i=1}^n\frac{-2x_i(yi-b)\Delta a+a^2{x}_i^2+x_i^{2}2a\Delta a+x_i^2\Delta a^2-a^2{x}_i^2}{\Delta a}\text{\hspace{1em}(3.10)}$$

$$\frac{\partial f}{\partial a}=\lim \sum _{i=1}^n-2x_i(y_i-b)+x_i^{2}2a+x_i^2\Delta a\text{\hspace{1em}(3.11)}$$

$$\frac{\partial f}{\partial a}=\lim \sum _{i=1}^{n}2x_i^{2}a-2x_i{y}_i+2x_{i}b\text{\hspace{1em}(3.12)}$$

$$\frac{\partial f}{\partial a}=\lim \sum _{i=1}^{n}2x_i(x_{i}a-y_i+b)\text{\hspace{1em}(3.13)}$$

$$\frac{\partial f}{\partial a}=-2\lim \sum _{i=1}^n{x}_i(y_i-x_{i}a-b))\text{\hspace{1em}(3.14)}$$

对 b 求偏导

$$\frac{\partial f}{\partial b}=\underset{\Delta b\to 0}{\lim }\sum _{i=1}^n\frac{(yi-(a{x}_i+(b+\Delta b){)}^2-(y_i-(a{x}_i+b){)}^2}{\Delta b}\text{\hspace{1em}(4.1)}$$

$$\frac{\partial f}{\partial b}=\underset{\Delta b\to 0}{\lim }\sum _{i=1}^n\frac{((y_i-a{x}_i)-(b+\Delta b){)}^2-((y_i-a{x}_i)-b){)}^2}{\Delta b}\text{\hspace{1em}(4.2)}$$

$$\frac{\partial f}{\partial b}=\underset{\Delta b\to 0}{\lim }\sum _{i=1}^n\frac{(y_i-a{x}_i{)}^2-2(y_i-a{x}_i)(b+\Delta b)+(b+\Delta b{)}^2-(y_i-a{x}_i{)}^2+2(y_i-a{x}_i)b-b^2}{\Delta b}\text{\hspace{1em}(4.3)}$$

$$\frac{\partial f}{\partial b}=\underset{\Delta b\to 0}{\lim }\sum _{i=1}^n\frac{\Delta b^2+2b\Delta b-2(y_i-a{x}_i)\Delta b}{\Delta b}\text{\hspace{1em}(4.4)}$$

$$\frac{\partial f}{\partial b}=\underset{\Delta b\to 0}{\lim }\sum _{i=1}^{n}2b-2(y_i-a{x}_i)\text{\hspace{1em}(4.5)}$$

$$\frac{\partial f}{\partial b}=\underset{\Delta b\to 0}{\lim }\sum _{i=1}^{n}2(b+a{x}_i-y_i)\text{\hspace{1em}(4.6)}$$

参考最小二乘法推导