题目描述

题目链接：AcWing 243. 一个简单的整数问题2
给定一个长度为 N 的数列 A，以及 M 条指令，每条指令可能是以下两种之一：

C l r d，表示把 A[l],A[l+1],…,A[r] 都加上 d。
Q l r，表示询问数列中第 l∼r 个数的和。
对于每个询问，输出一个整数表示答案。

输入格式

第一行两个整数 N,M。

第二行 N 个整数 A[i]。

接下来 M 行表示 M 条指令，每条指令的格式如题目描述所示。

输出格式

对于每个询问，输出一个整数表示答案。

每个答案占一行。

数据范围

1 ≤ N, M ≤ $10^5$,
|d| ≤ 10000,
|A[i]| ≤ $10^9$

输入示例

10 5
1 2 3 4 5 6 7 8 9 10
Q 4 4
Q 1 10
Q 2 4
C 3 6 3
Q 2 4

输出示例

4
55
9
15

思路分析

树状数组模板题，但是需要好好地分析：
1、最重要的一点，区间修改，所以一定用到差分
2、然后再来看，假设b数组是a数组的差分，那么就很简单地推出
a[1] = b[1]
a[2] = b[1] + b[2]
a[3] = b[1] + b[2] + b[3] …

在此基础上要求a[l] + a[l + 1] + … + a[r]，
这种求区间的很直观，使用前缀和解决，即：
a[l] + a[l + 1] + … + a[r] = (a[1] ~ a[r]) - (a[1] ~ a[l - 1])

所以，再找a[1] + a[2] + … + a[x]是多少呢？如图，是所有红色数的和

我们发现这其实是一个二维的矩阵，通过补齐可以看到：

此时a[1] + a[2] + a[3] + … + a[x]
= $(n+1)\ast {\sum }_1^x{b}_i-(b_1+2b_2+3b_3+...+x\ast b_x)$
= $(n+1)\ast {\sum }_1^x{b}_i-{\sum }_1^{x}i{b}_i$

所以只需维护好$b_i$和$i{b}_i$的前缀和即可

3、一些问题：
上面二维数组并不是对称的，不可以直接除以2，仔细发现对于每个$b_i$（即每一列中），除了最中间的列，其余列红色和黑色部分的个数都是不一样的

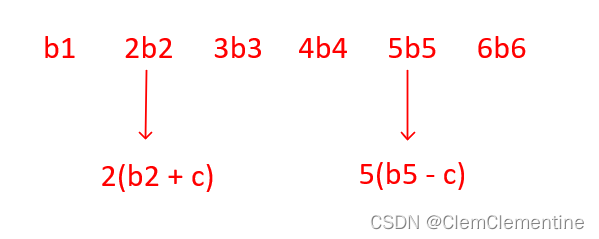
$i{b}_i$的维护会麻烦一些，因为变化的是$b_i$，所以记得加减系数

代码

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;
using LL = long long;
const int N = 1e5 + 10;
int n, m;
LL a[N], tr1[N], tr2[N];

int lowbit(int x) {
    return x & -x;
}

void add(LL tr[], int x, LL c) {
    for (int i = x; i <= n; i += lowbit(i))
        tr[i] += c;
}

LL query(LL tr[], int x) {
    LL res = 0;
    for (int i = x; i; i -= lowbit(i))
        res += tr[i];
    return res;
}

LL get_sum(int x) {
    return (x + 1) * query(tr1, x) - query(tr2, x);
}

int main()
{
    cin >> n >> m;
    for (int i = 1; i <= n; i++) {
        cin >> a[i];
        int b = a[i] - a[i - 1];
        add(tr1, i, b);
        add(tr2, i, (LL)b * i);    
    }

        
    
    while(m--) {
        char ch;
        LL l, r, d;
        cin >> ch >> l >> r;
        if(ch == 'C') {
            cin >> d;
            // a[l] += d
            add(tr1, l, d), add(tr2, l, l * d);
            // a[r + 1] -= d
            add(tr1, r + 1, -d), add(tr2, r + 1, (r + 1) * -d);
        }else {
            cout << get_sum(r) - get_sum(l - 1) << endl;
        }
    }
    return 0;
}