一、时间复杂度

算法（Algorithm）是指用来操作数据、解决程序问题的一组方法。

衡量代码的好坏，包括两个非常重要的指标：

 1.运行时间；
 2.占用空间。

算法复杂度分为时间复杂度和空间复杂度。其作用： 时间复杂度是指执行算法所需要的计算工作量；而空间复杂度是指执行这个算法所需要的内存空间。

时间复杂度：

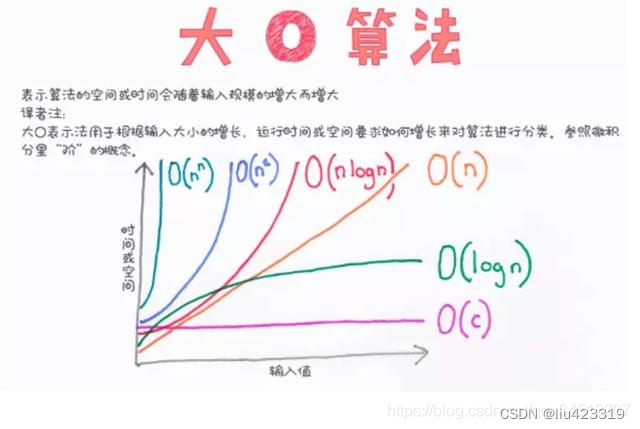
若存在函数 f(n)，使得当n趋近于无穷大时，T(n)/ f(n)的极限值为不等于零的常数，则称 f(n)是T(n)的同数量级函数。记作 T(n)= O(f(n))，称O(f(n)) ，全称为算法的渐进时间复杂度，简称时间复杂度。其中f(n) 表示每行代码执行次数之和，而 O 表示正比例关系。

时间复杂度用大写O来表示，所以也被称为大O表示法（也可读作big O）

如何推导出时间复杂度呢？有如下几个原则：

1.如果运行时间是常数量级，用常数1表示；

2.保留时间函数中的最高阶项；忽略低阶项

3.如果最高阶项存在，则忽略最高阶项的系数。

常见的时间复杂度量级有：

1 常数阶O(1)
2 对数阶O(logN)
3 线性阶O(n)
4 线性对数阶O(nlogN)
5 平方阶O(n²)
6 立方阶O(n³)
7 K次方阶O(n^k)
8 指数阶(2^n)

上面从上至下依次的时间复杂度越来越大，执行的效率越来越低。

常数阶O(1)：

无论代码执行了多少行，只要是没有循环等复杂结构，那这个代码的时间复杂度就都是O(1)，如：

int i = 1;
int j = 2;
++i;
j++;
int m = i + j;

上述代码在执行的时候，它消耗的时候并不随着某个变量的增长而增长，那么无论这类代码有多长，即使有几万几十万行，都可以用O(1)来表示它的时间复杂度。

对数阶O(logN):

int x = 1;
while(x< n)
{  
   x= x * 2;
   ......
}
1

由于每次count乘以2之后，就距离n更近了一分。由2^x=n 得到x=logn。所以这个循环的时间复杂度为O（logn）。二分查找时间复杂度也是O(logn)

线性阶O(n):

for(i=1; i<=n; ++i)
{
   j = i;
   j++;
}

这段代码，for循环里面的代码会执行n遍，因此它消耗的时间是随着n的变化而变化的，因此这类代码都可以用O(n)来表示它的时间复杂度。

线性对数阶O(nlogN)：
线性对数阶O(nlogN) 其实非常容易理解，将时间复杂度为O(logn)的代码循环N遍的话，那么它的时间复杂度就是 n * O(logN)，也就是了O(nlogN)。

就拿上面的代码加一点修改来举例：

for (x=1;x<=m;x++)
{
    i = 1;
    while(i<n)
    {
        i = i * 2;
    }
}

平方阶O(n²)：
平方阶O(n²) 就更容易理解了，如果把 O(n) 的代码再嵌套循环一遍，它的时间复杂度就是 O(n²) 了。
举例：

for(x=1; i<=n; x++)
{
   for(i=1; i<=n; i++)
    {
      ...
    }
}

这段代码其实就是嵌套了2层n循环，它的时间复杂度就是 O(n*n)，即 O(n²)
如果将其中一层循环的n改成m，即：

for(x=1; i<=m; x++)
{
   for(i=1; i<=n; i++)
    {
      ...
    }
}

那它的时间复杂度就变成了 O(m*n)

立方阶O(n³)、K次方阶O(n^k):
参考上面的O(n²) 去理解就好了，O(n³)相当于三层n循环，其它的类似。

指数阶 O(2ⁿ)：
指数阶的算法基本上已经很烂了，除非数据量很小，否则千万不要使用指数阶算法。

int fibRecur(N) {
  if(N <= 1) { // 递归终止条件
    return N;
  }
  return fibRecur(N - 1) + fibRecur(N - 2); // 向下递归
}

以上代码是一个递归算法的斐波那契数列解法，其时间复杂度为 O(2ⁿ)，也就是指数阶。

怎么证明的我就不放了我数学一般，网上有很多大佬对其进行了证明，感兴趣的可以自行查找。

二、空间复杂度

既然时间复杂度不是用来计算程序具体耗时的，那么我也应该明白，空间复杂度也不是用来计算程序实际占用的空间的。空间复杂度是对一个算法在运行过程中临时占用存储空间大小的一个量度，同样反映的是一个趋势，我们用 S(n) 来定义。

空间复杂度比较常用的有：O(1)、O(n)、O(n²)，我们下面来看看：

空间复杂度 O(1)

如果算法执行所需要的临时空间不随着某个变量n的大小而变化，即此算法空间复杂度为一个常量，可表示为 O(1)。

int i = 1;
int j = 2;
i++;
j++;
int m = i + j;

代码中的 i、j、m 所分配的空间都不随着处理数据量变化，因此它的空间复杂度 S(n) = O(1)。

空间复杂度 O(n)

int[] m = new int[n]
for(i = 1; i <= n; ++i) {
    j = i; 
    j++;
}

这段代码中，第一行new了一个数组出来，这个数据占用的大小为n，后面虽然有循环，但没有再分配新的空间，因此，这段代码的空间复杂度主要看第一行即可，即 S(n) = O(n)。

空间复杂度 O(n²)
一段代码，随着数据量的变化内存消耗呈平方变化的时候，空间复杂度为O(N²)。

int[][] arr = new int[n][n];
for(int i = 0; i < n; i++) {
  for(int j = 0; j < n; j++) {
    arr[i][j] = new Random().nextInt();
  }
}

总结

1 算法是用来解决某个问题（任务）的一组方法，在计算机领域中，它被描述为一系列的指令集合
2 时间复杂度：执行当前算法所消耗的时间
3 空间复杂度：执行当前算法需要占用的内存空间
4 无论是时间复杂度还是空间复杂度，考虑的都是问题规模 N 无限大的情况下，所需时间或所需空间变化的趋势
5 事实上，时间复杂度和空间复杂度描述的都是在问题规模无限大的情况下，所需时间或空间的增速
6 当问题规模 N 是有限的或很小的值，我们完全可以不考虑某个算法的时间复杂度或空间复杂度

三、排序算法

1.比较排序

1.1冒泡排序：

重复地走访过要排序的数列，每次比较相邻两个元素，如果它们的顺序错误就把它们交换过来，越大的元素会经由交换慢慢“浮”到数列的尾端。

时间复杂度为O(n²)，额外空间复杂度O(1)

下面添加过flag的是改良过的冒泡，有很多人说冒泡排序的最优的时间复杂度为：O(n)；就是因为在代码中使用一个flag来判断是否已经排序好，如果元素已经排序好，那么循环一次就直接退出；或者说元素开始就已经大概有序了，那么这种方法就可以很好减少排序的次数。严格来说时间复杂度为O(n²)。

动图演示：

public void bubbleSort(int[] arr) {
    int temp = 0;
    boolean swap;
    for (int i = arr.length - 1; i > 0; i--) { // 每次需要排序的长度
        // 增加一个swap的标志，当前一轮没有进行交换时，说明数组已经有序
        swap = false;
        for (int j = 0; j < i; j++) { // 从第一个元素到第i个元素
            if (arr[j] > arr[j + 1]) {
                temp = arr[j];
                arr[j] = arr[j + 1];
                arr[j + 1] = temp;
                swap = true;
            }
        }
        if (!swap){
            break;
        }
    }
}

1.2选择排序：

选择排序的思想其实和冒泡排序有点类似，都是在一次排序后把最小的元素放到最前面，或者将最大值放在最后面。但是过程不同，冒泡排序是通过相邻的比较和交换。而选择排序是通过对整体的选择，每一趟从前往后查找出无序区最小值，将最小值交换至无序区最前面的位置。

时间复杂度为O(n²)，额外空间复杂度O(1)

无论什么数据进去都是 O(n²) 的时间复杂度。所以用到它的时候，数据规模越小越好。唯一的好处可能就是不占用额外的内存空间了吧。

动图演示：

 public static void selectionSort(int[] arr){
        for(int i = 0; i < arr.length - 1; i++){//交换次数
            int minIndex = i; //先假设每次循环时，最小数的索引为i
            //每一个元素都和剩下的未排序的元素比较
            for(int j = i + 1; j < arr.length; j++){
                if(arr[j] < arr[minIndex]){//寻找最小数
                    minIndex = j;//将最小数的索引保存
                }
            }
            //经过一轮循环，就可以找出第一个最小值的索引，然后把最小值放到i的位置
            swap(arr, i, minIndex);
        }
    }
    private static void swap(int[] arr, int i, int j) {
        int temp = arr[i];
        arr[i] = arr[j];
        arr[j] = temp;
    }
    

1.3插入排序：

插入排序的代码实现虽然没有冒泡排序和选择排序那么简单粗暴，但它的原理应该是最容易理解的了，因为只要打过扑克牌的人都应该能够秒懂。插入排序是一种最简单直观的排序算法，它的工作原理是通过构建有序序列，对于未排序数据，在已排序序列中从后向前扫描，找到相应位置并插入。

插入排序的平均时间复杂度也是 O(n²)，空间复杂度为常数阶 O(1)

当待排序数组是有序时，是最优的情况，时间复杂度为O(n);
最坏的情况是待排序数组是逆序的，此时需要比较次数最多，时间复杂度O(n);
平均来说，A[1…j-1]中的一半元素小于A[j]，一半元素大于A[j]。插入排序在平均情况运行时间与最坏情况运行时间一样，是输入规模的二次函数 。

但是算法都是按最差情况评估时间复杂度，所以一般来说，插入排序时间复杂度也是 O(n²)

动图演示：

   public static void insertSort(int[] arr) {
        for (int i = 1; i < arr.length; i++) {
            for (int j = i - 1; j > 0 && arr[j] > arr[j + 1]; j--) {
                swap(arr, j, j+1);
            }
        }
    }

    private static void swap(int[] arr, int i, int j) {
        int t = arr[i];
        arr[i] = arr[j];
        arr[j] = t;
    }

1.4归并排序(非常重要)

这是我们目前第一个时间复杂度O(n*logn)的算法，比O(n²)算法要好很多

但是，在这之前，我们要先了解下递归
例子1：1-100之和

//普通方法for循环
public int sum(){
	int sum=0;
	for(int i=1;i<=100;i++){
		sum+=i;
	}
	return sum;
}
//递归方法
//求从1加到n的和；
/*
n=1 ,1
n=2, 2+sum(1)
n=3, 3+sum(2)
n,n+sum(n-1);
*/
public static int sum(int n){
	if(n==1){
		return 1;
	}
	return n+sum(n-1);
}

递归的缺点：当递归数量较大时会大量占用栈的内存，运行性能不如for循

例子2：斐波那契数列

这个数列从第3项开始，每一项都等于前两项之和;且第一项为0，第二项为1。

0、1、1、2、3、5、8、13、21、34.....
表达式：F[n]=F[n-1]+F[n-2](n>=2,F[0]=0,F[1]=1)

用java实现：

public static long fibonacci(long number) {
        if ((number == 0) || (number == 1))
            return number;
        else
            return fibonacci(number - 1) + fibonacci(number - 2);
    }

例子3：求最大值

public static int  getMax(int [] arr,int L,int R) {
		if (L==R) {
			return arr[L];
		}else {
			int mid=(L+R)/2;
			int leftMax=getMax(arr, L, mid);
			int rightMax=getMax(arr, mid+1, R);
			return Math.max(leftMax, rightMax);
		}
	}

递归行为时间复杂度估算：master公式:（非常重要）

T(n) = a*T(n/b) + O (n^d)

T(n)指的是样本量为n的情况下的时间复杂度；n/b指的是递归子过程的样本量（一个父问题划分为n/b个子问题，子问题样本量肯定比父问题样本量小，这里只用看父问题划分为子问题的第一步即可，比如上面的求最大值，aT(n/b)就是2T(n/2)）；a指的是子过程发生的次数；O (n^d)指的是除了子过程调用外剩下的过程的时间复杂度（比如单纯的大小比较）。
所以上面求最大值的时间复杂度为T(n) = 2T(n/2) + O (1)；因为除了子过程调用外，剩余的就是比较大小，是一个常数操作，也就是O(1)。
即：T(n) = 2T(n/2) + O (n^0)；a=2，b=2，d=0。用下面的公式计算，时间复杂度为：
O(n^log(b,a))==>O(n)。

满足master公式的，有一个固定解法：

1) log(b,a) > d -> 复杂度为O(n^log(b,a))
2) log(b,a) = d -> 复杂度为O(n^d * logn)
3) log(b,a) < d -> 复杂度为O(n^d)

归并排序：
时间复杂度为O(n*logn)
分解待排序的数组成两个各具 n/2 个元素的子数组，递归调用归并排序两个子数组，合并两个已排序的子数组成一个已排序的数组。

归并排序思路简单，速度仅次于快速排序，为稳定排序算法，一般用于对总体无序，但是各子项相对有序的数列。

动图演示：

public static void mergeSort(int[] arr) {
		if (arr == null || arr.length < 2) {
			return;
		}
		mergeSort(arr, 0, arr.length - 1);
	}

	public static void mergeSort(int[] arr, int l, int r) {
		if (l == r) {//这个范围上只有一个数
			return;
		}
		int mid = l + ((r - l) >> 1); //等同于l+(r-l)/2
		mergeSort(arr, l, mid);	//T(n/2)
		mergeSort(arr, mid + 1, r);//T(n/2)
		merge(arr, l, mid, r);//O(n)
	}

	public static void merge(int[] arr, int l, int m, int r) {
		int[] help = new int[r - l + 1];//辅助数组
		int i = 0;
		int p1 = l; //左侧第一个数
		int p2 = m + 1; //右侧第一个数
		while (p1 <= m && p2 <= r) {//谁小选谁，然后辅助数组和选中的数组下标移动一个位置
			help[i++] = arr[p1] < arr[p2] ? arr[p1++] : arr[p2++];
		}
		while (p1 <= m) {//拷贝剩余的（这2个while只会走一个）
			help[i++] = arr[p1++];
		}
		while (p2 <= r) {//拷贝剩余的
			help[i++] = arr[p2++];
		}
		for (i = 0; i < help.length; i++) {//辅助数组拷贝回原数组
			arr[l + i] = help[i];
		}
	}

时间复杂度计算 :T(n)=2T(n/2)+O(n)；代入master公式计算得：O(n * logn)
所以归并排序的时间复杂度为：O(n logn)，额外的空间复杂度：O(n)

注意：关于取中间值为什么说 l + ((r - l) >> 1） 优于 l+(r-l)/2，l+(r-l)/2优于**(l+r)/2**？

mid = (l + r) / 2的最大劣势就是有溢出可能：l + r可能会溢出int的最大范围，而l + (r - l) / 2不会，这里用减法替代了加法，这种思想很多地方都有用到。

	int x = 1999999998;
    int y = 1999999998;
    int mid = (x+y) / 2;
    int mid2 = x + (y-x) / 2;
    System.out.println(mid);    //-147483650
    System.out.println(mid2);  //1999999998

而位运算比算术运算快很多。虽然都是常数的，但是位运算的常数项要小。也就是说时间复杂度的指标是一样的，但相对来说位运算更好。

**两个经典的算法题：**小和问题和逆序对问题

1.小和问题
在一个数组中，每一个数左边比当前数小的数累加起来，叫做这个数组的小和。求一个数组的小和。
例子： [1,3,4,2,5]
1左边比1小的数，没有；
3左边比3小的数，1；
4左边比4小的数，1、3；
2左边比2小的数，1；
5左边比5小的数，1、3、4、2；
所以小和为1+1+3+1+1+3+4+2=16

解题思路
如果直接用两层for循环扫，时间复杂度是O(n²)；但是可以通过归并排序的方法将时间复杂度降到O(nlogn)

这道题换个角度来想，题目要求的是每个数左边有哪些数比自己小，其实不就是右边有多少个数比自己大，那么产生的小和就是当前值乘以多少个吗？

用归并排序来解：

public static int smallSum(int[] arr) {
		if (arr == null || arr.length < 2) {
			return 0;
		}
		return mergeSort(arr, 0, arr.length - 1);
	}

	public static int mergeSort(int[] arr, int l, int r) {
		if (l == r) {
			return 0;
		}
		int mid = l + ((r - l) >> 1);
		return mergeSort(arr, l, mid) 	// 左侧产生的小和
		+ mergeSort(arr, mid + 1, r) 	// 右侧产生的小和
		+ merge(arr, l, mid, r);		// merge过程中产生的小和
	}

	public static int merge(int[] arr, int l, int m, int r) {
		int[] help = new int[r - l + 1];
		int i = 0;
		int p1 = l;
		int p2 = m + 1;
		int res = 0;
		while (p1 <= m && p2 <= r) {
			res += arr[p1] < arr[p2] ? (r - p2 + 1) * arr[p1] : 0;
			help[i++] = arr[p1] < arr[p2] ? arr[p1++] : arr[p2++];
		}
		while (p1 <= m) {
			help[i++] = arr[p1++];
		}
		while (p2 <= r) {
			help[i++] = arr[p2++];
		}
		for (i = 0; i < help.length; i++) {
			arr[l + i] = help[i];
		}
		return res;
	}

2.逆序对问题
在一个数组中，左边的数如果比右边的数大，则这两个数构成一个逆序对，请打印所有逆序对。
同上面小和问题，也可以用归并来解。还可以利用树状数组求解

1.5快速排序（非常重要）

学快排之前先看一个荷兰国旗问题（partition）。
荷兰国旗是由红白蓝3种颜色的条纹拼接而成，如下图所示：

假设这样的条纹有多条，且各种颜色的数量不一，并且随机组成了一个新的图形，比如：

半部分，我们把这类问题称作荷兰国旗问题。

例：给定一个数组arr，和一个数num，请把小于num的数放在数组的左边，等于num的数放在数组的中间，大于num的数放在数组的右边。
要求额外空间复杂度O(1)，时间复杂度O(N)

	/**
	 * 在指定的数组角标范围内，完成荷兰国旗问题
	 * @param arr 		需要处理的数组
	 * @param l   		需要处理的数组范围-左侧角标
	 * @param r	  		需要处理的数组范围-右侧角标
	 * @param num   	给定的数
	 * @return    		返回等与区域的左右边界角标组成的数组
	 */
	public static int[] partition(int[] arr, int l, int r, int num) {
		int less = l - 1;
		int more = r + 1;
		while (l < more) {
			if (arr[l] < num) {
				swap(arr, ++less, l++);//放到小于区域，当前位置和小于区域的下一个数交换;然后当前位置走到下一个，l++
			} else if (arr[l] > num) {
				swap(arr, --more, l);//放到大于区域，当前位置和大于区域的前一个数交换，由于换过来的大于区域的值不确定是多大，所以当前位置l不变,继续比较
			} else {
				l++;	//=num相等则直接跳到下一个位置
			}
		}
		return new int[] { less + 1, more - 1 };//返回等与区域的左右边界角标组成的数组
	}
	
	public static void swap(int[] arr, int i, int j) {
		int tmp = arr[i];
		arr[i] = arr[j];
		arr[j] = tmp;
	}
	
	public static void printArray(int[] arr) {
		if (arr == null) {
			return;
		}
		for (int i = 0; i < arr.length; i++) {
			System.out.print(arr[i] + " ");
		}
		System.out.println();
	}

快速排序：
经典快排：
默认每次以数组最后一个数字来划分。把目标值放在中间，左边都是小于等于它的，右边是大于它的值。两边各自拿去递归。

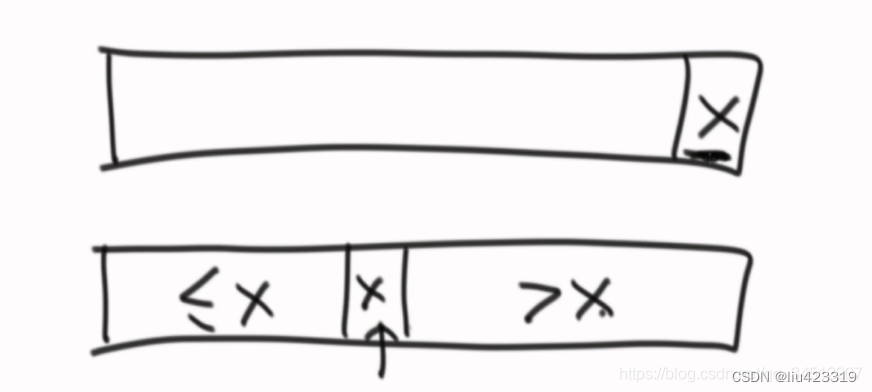
也就是每次只搞定了一个数，X。因为左侧小于区域也可能包含X，但会拿去进行下一轮递归操作。

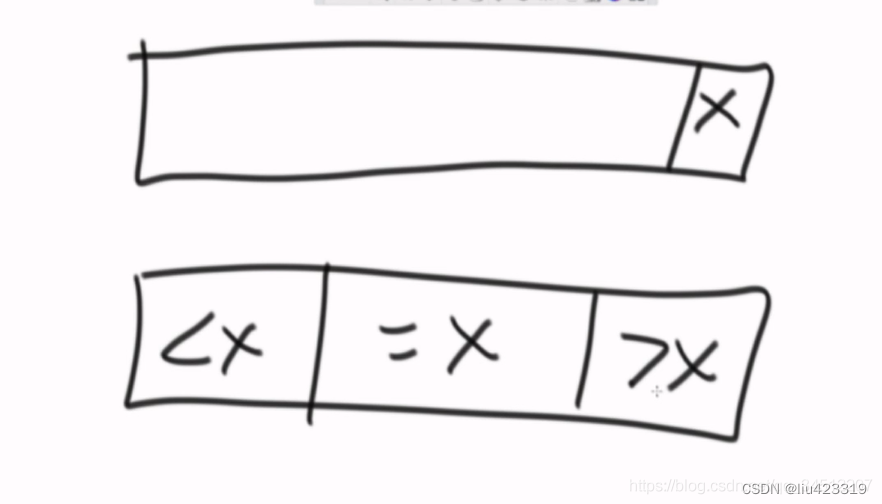
改进后的经典快排：
默认每次以数组最后一个数字来划分。用荷兰国旗思想改进，就划分为3个区域，小于，等于，大于。以避免等于的数字经过多次划而分浪费时间。

	public static void quickSort(int[] arr) {
		if (arr == null || arr.length < 2) {
			return;
		}
		quickSort(arr, 0, arr.length - 1);
	}
	// 是数组arr在l~r的范围内有序 
	public static void quickSort(int[] arr, int l, int r) {
		if (l < r) {//递归能发生的条件
			swap(arr, l + (int) (Math.random() * (r - l + 1)), r);//加上这行，就是随机快排。每次选的数据不是数组最后的数字，而是随机的
			int[] p = partition(arr, l, r);
			quickSort(arr, l, p[0] - 1);
			quickSort(arr, p[1] + 1, r);
		}
	}

	public static int[] partition(int[] arr, int l, int r) {
		int less = l - 1;
		int more = r;
		while (l < more) {
			if (arr[l] < arr[r]) {
				swap(arr, ++less, l++);
			} else if (arr[l] > arr[r]) {
				swap(arr, --more, l);
			} else {
				l++;
			}
		}
		swap(arr, more, r);//数组最后一个数和大于区域前一个数（是一定存在的）互换位置。
		return new int[] { less + 1, more };//返回的是等于区域的左右边界
	}

	public static void swap(int[] arr, int i, int j) {
		int tmp = arr[i];
		arr[i] = arr[j];
		arr[j] = tmp;
	}

经典快排的问题：划分出来的区域容易打偏（非常容易举出反例，如{6，5，4，3，2，1}）；时间复杂度最差为O(n²)。最佳情况为O(logn)。

随机快排：每次不用数组最后一个数来划分，而是随机选择一个数与数组最后一个数交换位置。虽然也可能打偏，但是复杂度会成为一个概率时间，用长期期望的方式来计算，时间复杂度为O(logn)（数学家证明好了，哈哈。其实这里我不是很理解，因为从概率上看随机快排也可能每次都打偏；但是反过来看，随机快排想举出反例却不好举了，那那那就相信数学家吧）

许多编程语言的内部元素排序实现中采用的就是快速排序，很多面试题中也经常遇到。
随机快排的时间复杂度是：O(logn)；额外空间复杂度是：O(logn)

1.6堆排序

先看两个概念：满二叉树和完全二叉树

完全二叉树：设二叉树的深度为h，除第 h 层外，其它各层 (1～h-1) 的结点数都达到最大个数，
第 h 层所有的结点都连续集中在最左边

满二叉树：深度为k且有2^k-1个结点的二叉树称为满二叉树

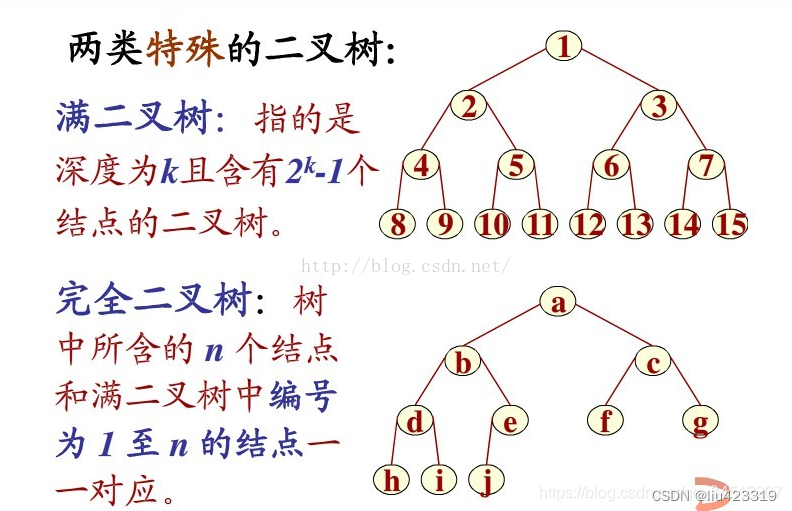
弄明白这个就很方便理解堆排序。

堆排序（Heapsort）是指利用堆这种数据结构所设计的一种排序算法。堆积是一个近似完全二叉树的结构，并同时满足堆积的性质：即子结点的键值或索引总是小于（或者大于）它的父节点。堆排序可以说是一种利用堆的概念来排序的选择排序。

分为两种方法：
大根堆：每个节点的值都大于或等于其子节点的值，在堆排序算法中用于升序排列；
小根堆：每个节点的值都小于或等于其子节点的值，在堆排序算法中用于降序排列；

堆排序的平均时间复杂度为 Ο(nlogn)。

父节点：（i - 1）/ 2
左节点：（2 * i）+1
右节点：（2 * i）+2

思路：
1.让数组形成大根堆，数组还是无序状态；但是此时堆顶一定是数组的最大值。（一般升序采用大根堆，降序采用小根堆)。
2.堆最后一个位置的数与堆顶交换，使末尾元素最大。heapsize减1。
3.剩下的heapsize范围中做heapify操作，重新生成大根堆。重复23操作，直到数组全部有序。

public static void heapSort(int[] arr) {
		if (arr == null || arr.length < 2) {
			return;
		}
		for (int i = 0; i < arr.length; i++) {
			heapInsert(arr, i); //形成大根堆
		}
		int size = arr.length;  //heapSize初始为数组长度
		swap(arr, 0, --size);  //交换堆顶和堆结构最后一个数，size-1
		while (size > 0) {
			heapify(arr, 0, size);  //交换完后下沉操作再次形成大根堆
			swap(arr, 0, --size);  //重复交换
		}
	}
	//将数组建立成大根堆，时间复杂度为O(N)
	public static void heapInsert(int[] arr, int index) {
		while (arr[index] > arr[(index - 1) / 2]) {
			swap(arr, index, (index - 1) / 2);
			index = (index - 1) / 2;
		}
	}
	//一个值变小后，往下沉的操作。
	public static void heapify(int[] arr, int index, int size) {
		int left = index * 2 + 1;
		while (left < size) {
			//左右孩子谁大，谁的下标作为largest
			int largest = left + 1 < size && arr[left + 1] > arr[left] ? left + 1 : left;
			//左右孩子较大的和当前index位置比较，谁大谁的下标作为largest 
			largest = arr[largest] > arr[index] ? largest : index;
			if (largest == index) {//和孩子比较自己最大，说明不用往下沉了
				break;
			}
			swap(arr, largest, index);//交换，接着进行下一轮while,直到越界或者不需要下沉
			index = largest;			
			left = index * 2 + 1;
		}
	}

	public static void swap(int[] arr, int i, int j) {
		int tmp = arr[i];
		arr[i] = arr[j];
		arr[j] = tmp;
	}

时间复杂度O(N*logN)，额外空间复杂度O(1)

堆结构非常重要

1，堆结构的heapInsert与heapify
2，堆结构的增大和减少
3，如果只是建立堆的过程，时间复杂度为O(N)
4，优先级队列结构，就是堆结构

1.7排序算法稳定性

假定在待排序的记录序列中，存在多个具有相同的关键字的记录，若经过排序，这些记录的相对次序保持不变，即在原序列中，r[i]=r[j]，且r[i]在r[j]之前，而在排序后的序列中，r[i]仍在r[j]之前，则称这种排序算法是稳定的；否则称为不稳定的。

「稳定性」有何意义？

如果我们只是面对简单的数字排序，那么稳定性确实也没有多大意义。比如，1 2 3 3 4的序列中如果第一个3和第二个3在sort方法反复执行之后位置也反复变化，但是对于调用sort方法所想要获得排序结果的上游应用而言，那么结果还是1 2 3 3 4，至于3的次序，无关紧要。

如果要排序的内容是一个复杂对象的多个数字属性，但是其原本的初始顺序毫无意义，那么稳定性依旧将毫无意义。

那么排序算法的「稳定性」在什么情况下才会变得有意义呢？

举个例子，一个班的学生已经按照学号大小排好序了，我现在要求按照年龄从小到大再排个序，如果年龄相同的，必须按照学号从小到大的顺序排列。那么问题来了，你选择的年龄排序方法如果是不稳定的，是不是排序完了后年龄相同的一组学生学号就乱了，你就得把这组年龄相同的学生再按照学号拍一遍。如果是稳定的排序算法，我就只需要按照年龄排一遍就好了。

从一个键上排序，然后再从另一个键上排序，第一个键排序的结果可以为第二个键排序所用。要排序的内容是一个复杂对象的多个数字属性，且其原本的初始顺序存在意义，那么我们需要在二次排序的基础上保持原有排序的意义，才需要使用到稳定性的算法。

排序算法的「稳定性」在很多情况下，并没有什么实质的意义，而在有些情况下却有很重要的意义。

有很多算法你现在看着没啥，但是当放在大数据云计算的条件下它的稳定性非常重要。举个例子来说，对淘宝网的商品进行排序，按照销量，价格等条件进行排序，它的数据服务器中的数据非常多，因此，当时用一个稳定性效果不好的排序算法，如堆排序、shell排序，当遇到最坏情形，会使得排序的效果非常差，严重影响服务器的性能，影响到用户的体验。

堆排序、快速排序、希尔排序、直接选择排序是不稳定的排序算法，而冒泡排序、直接插入排序、折半插入排序、归并排序是稳定的排序算法。

有关排序问题的补充： 1，归并排序的额外空间复杂度可以变成O(1)，但是非常难，不 需要掌握，可以搜“归并排序 内部缓存法” 2，快速排序可以做到稳定性问题，但是非常难，不需要掌握， 可以搜“01 stable sort” 3，有一道题目，是奇数放在数组左边，偶数放在数组右边，还 要求原始的相对次序不变，碰到这个问题，可以怼面试官。面试 官非良人

2.线性排序

桶排序、计数排序、基数排序

1，非基于比较的排序，与被排序的样本的实际数据状况很有关系，所以实际中并不经常使用 
2，时间复杂度O(N)，额外空间复杂度O(N) 
3，稳定的排序

2.1桶排序

		// only for 0~200 value
		public static void bucketSort(int[] arr) {
			if (arr == null || arr.length < 2) {
				return;
			}
			int max = Integer.MIN_VALUE;
			for (int i = 0; i < arr.length; i++) {
				max = Math.max(max, arr[i]);
			}
			int[] bucket = new int[max + 1];
			for (int i = 0; i < arr.length; i++) {
				bucket[arr[i]]++;
			}
			int i = 0;
			for (int j = 0; j < bucket.length; j++) {
				while (bucket[j]-- > 0) {
					arr[i++] = j;
				}
			}
		}

2.2计数排序

桶排序严格说不能算一种具体的排序，只是一种大的逻辑概念，有各种各样的实现方式。而计数排序可以理解为桶排序的一种具体实现。作为一种线性时间复杂度的排序，计数排序要求输入的数据必须是有确定范围的整数，也就是说适用范围很窄。

计数排序的核心在于将输入的数据值转化为键存储在额外开辟的数组空间中。

如下图：

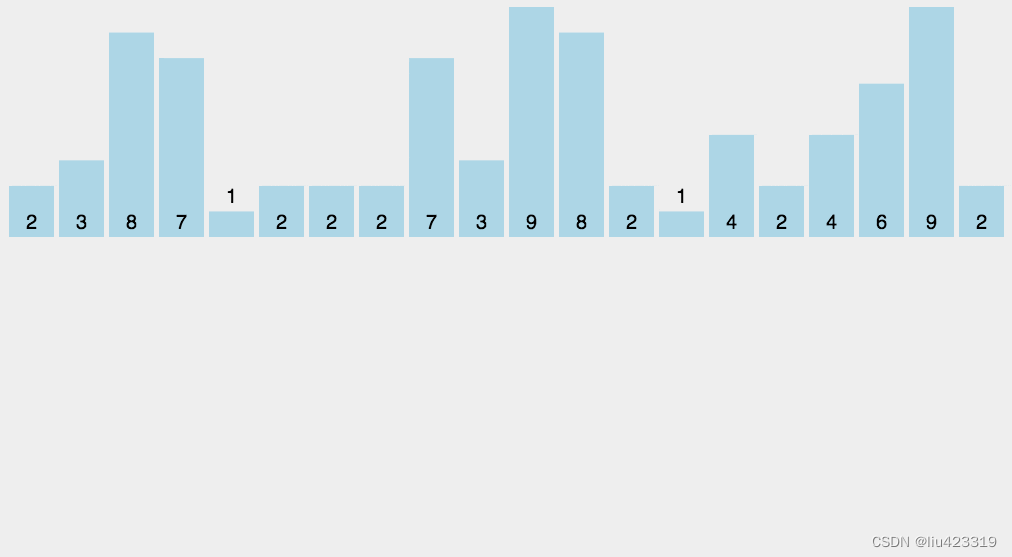
public void countSort(int[] arr) {
    int max = Integer.MIN_VALUE;
    int min = Integer.MAX_VALUE;
    for(int i = 0; i < arr.length; i++){//找出数组中最大值和最小值
        max = Math.max(max, arr[i]);
        min = Math.min(min, arr[i]);
    }

    int[] b = new int[arr.length]; 		// 存储数组
    int[] count = new int[max - min + 1]; // 计数数组

    for (int num = min; num <= max; num++) { //count数组初始化各元素值为0（元素个数为max-min+1）
        count[num - min] = 0;
    }
	
    for (int i = 0; i < arr.length; i++) {//每个元素数量计数
        int num = arr[i];
        count[num - min]++; // 每出现一个值，计数数组对应元素的值+1
        // 此时count[i]表示数值等于i的元素的个数
    }

    for (int i = min + 1; i <= max; i++) {
        count[i - min] += count[i - min - 1];
        // 此时count[i]表示数值<=i的元素的个数
    }

    for (int i = 0; i < arr.length; i++) {
            int num = arr[i]; // 原数组第i位的值
            int index = count[num - min] - 1; //加总数组中对应元素的下标
            b[index] = num; // 将该值存入存储数组对应下标中
            count[num - min]--; // 加总数组中，该值的总和减少1。
    }

    // 将存储数组的值替换给原数组
    for(int i=0; i < arr.length;i++){
        arr[i] = b[i];
    }
}

t经典题：相邻两数最大差值：给定一个数组，求如果排序之后，相邻两数的最大差值，要求时间复杂度O(N)，且要求不能用非基于比较的排序。

这里是一种非常巧妙的算法解决该问题。
思路：

1.假如数组中有n个数，遍历一遍数组得到数组中的最大值max，最小值min，然后我们为这n个数准备n+1个桶来装这n个数。

2.若min等于max，则说明数组中的这9个数都是一样的，那立马返回相邻两数的最大差值为0.

3.若min不等于max，此刻假设min=0，max=99，然后因为数组有9个数，那桶的数量就为10个。

4.再从头开始遍历数组，数组中的最小值一定进入0号桶，数组中的最大值一定进入9号桶，数组中的其他元素也依次进对应的桶，并且每个桶中只需要保留最大和最小的数，以及是否进来过数字即可。

5.那就是，9个数，10个桶，遍历完一轮数组之后，其中第一个桶和最后一个桶一定不为空，而且，中间的桶必定至少有一个桶是空桶！

6.相邻两个桶的差值就是后一个桶的最小值 - 前一个桶的最大值；最大差值一定是相邻两个桶之间的差值中最大的一个。

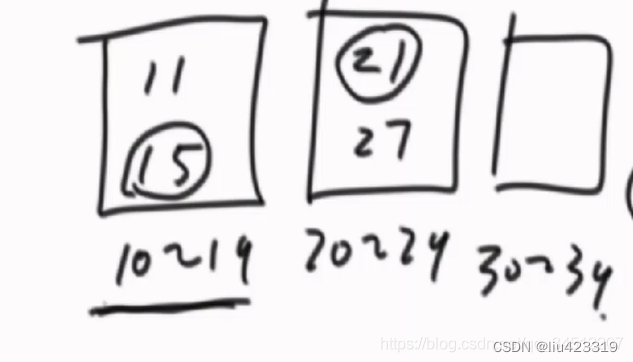
public static int maxGap(int[] nums) {
		if (nums == null || nums.length < 2) {
			return 0;
		}
		int len = nums.length;  
		int min = Integer.MAX_VALUE; //最小值设为系统最大值
		int max = Integer.MIN_VALUE; //最大值设为系统最小值
		for (int i = 0; i < len; i++) {//for找出数组中最大值和最小值
			min = Math.min(min, nums[i]);
			max = Math.max(max, nums[i]);
		}
		if (min == max) {
			return 0;
		}
		//三个长度为 len + 1 的数组，即0号桶到 len + 1 号桶的三个信息
		boolean[] hasNum = new boolean[len + 1];	//桶中是否有数
		int[] maxs = new int[len + 1];				//桶中数的最大值
		int[] mins = new int[len + 1];				//桶中数的最小值
		int bid = 0;
		for (int i = 0; i < len; i++) {//确定当前数属于几号桶，并改变该桶的最大值，最小值，以及确定是否有数
			bid = bucket(nums[i], len, min, max);
			mins[bid] = hasNum[bid] ? Math.min(mins[bid], nums[i]) : nums[i];
			maxs[bid] = hasNum[bid] ? Math.max(maxs[bid], nums[i]) : nums[i];
			hasNum[bid] = true;
		}
		int res = 0;//记录最大差值
		int lastMax = maxs[0];//记录前一个桶的最大值
		int i = 1;
		//找到每个非空桶，和它左边理它最近的非空桶。计算差值
		for (; i <= len; i++) {
			if (hasNum[i]) {
				res = Math.max(res, mins[i] - lastMax);//计算相邻两个桶的最大差值，并记录整个桶结构中的最大差值
				lastMax = maxs[i];
			}
		}
		return res;
	}

//确定当前数属于几号桶	
public static int bucket(long num, long len, long min, long max) {
		return (int) ((num - min) * len / (max - min));
	}

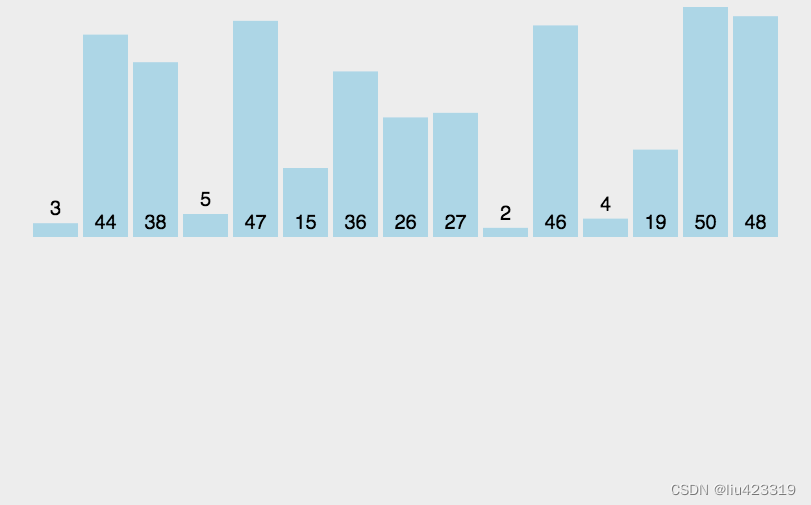
第一次看这个代码，有个疑问，为什么不直接找到空桶两侧的非空桶，他们两个之间的最大差值不就是整个桶结构中的最大差值吗？

如下图：

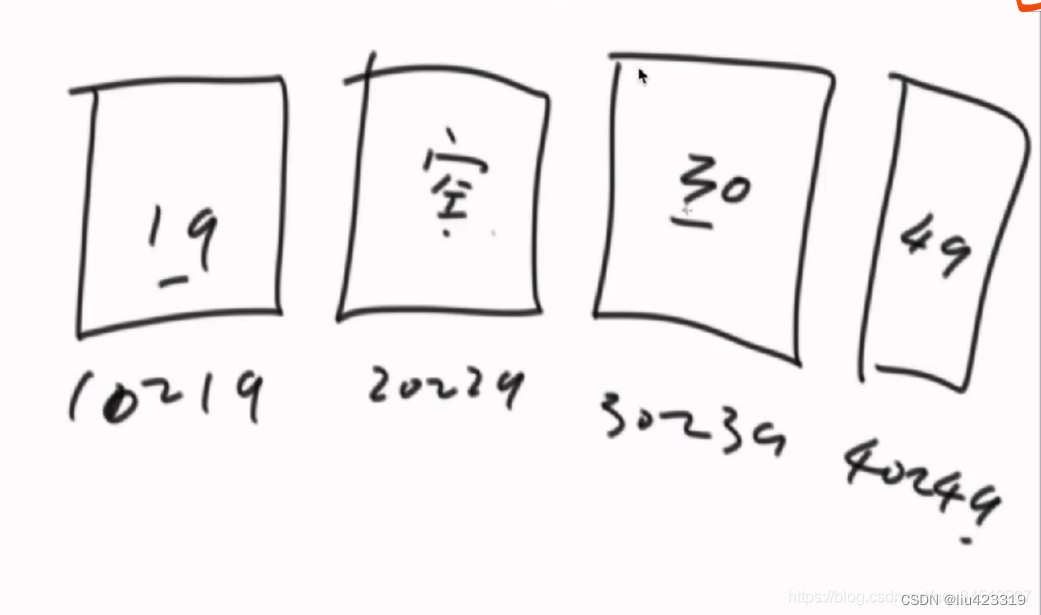
很明显，最大差值并不是来自空桶2侧的非空桶

设计一个空桶的分析方式在于：最大差值一定不来自一个桶的内部；也就是一个桶内部的差值一定不是我们需要的答案（因为有空桶的存在，空桶两侧非空桶的差值一定会比任意一个桶内部的差值要大），但是并不代表空桶两侧的非空桶之间的差值就是我们需要的答案

2.3基数排序

// only for no-negative value
		public static void radixSort(int[] arr) {
			if (arr == null || arr.length < 2) {
				return;
			}
			radixSort(arr, 0, arr.length - 1, maxbits(arr));
		}

		public static int maxbits(int[] arr) {
			int max = Integer.MIN_VALUE;
			for (int i = 0; i < arr.length; i++) {
				max = Math.max(max, arr[i]);
			}
			int res = 0;
			while (max != 0) {
				res++;
				max /= 10;
			}
			return res;
		}

		public static void radixSort(int[] arr, int begin, int end, int digit) {
			final int radix = 10;
			int i = 0, j = 0;
			int[] count = new int[radix];
			int[] bucket = new int[end - begin + 1];
			for (int d = 1; d <= digit; d++) {
				for (i = 0; i < radix; i++) {
					count[i] = 0;
				}
				for (i = begin; i <= end; i++) {
					j = getDigit(arr[i], d);
					count[j]++;
				}
				for (i = 1; i < radix; i++) {
					count[i] = count[i] + count[i - 1];
				}
				for (i = end; i >= begin; i--) {
					j = getDigit(arr[i], d);
					bucket[count[j] - 1] = arr[i];
					count[j]--;
				}
				for (i = begin, j = 0; i <= end; i++, j++) {
					arr[i] = bucket[j];
				}
			}
		}

		public static int getDigit(int x, int d) {
			return ((x / ((int) Math.pow(10, d - 1))) % 10);
		}