一、前言

前面学习了SS算法、R-CNN网络，接下来继续学习Fast-RCNN网络。
在这里插入图片描述

本文两个目的，其一作为个人笔记，方便自己巩固复习知识；其二帮助正在自学的朋友，希望拙劣的见解可以帮助到大家。

二、Fast-RCNN原理步骤

Fast-RCNN可以分为三个步骤：

1)使用SS算法生成大概1-2k的候选框。
2)参考SPPnet模型来将整张图片输入网络得到特征图，再将第一步得到的候选框映射到特征矩阵来提取特征矩阵。
3）特征层通道ROI pooling操作缩放到7*7大小，展平连接一系列的全连接层得到分类结果和边界框回归参数。

2.1候选区域的生成

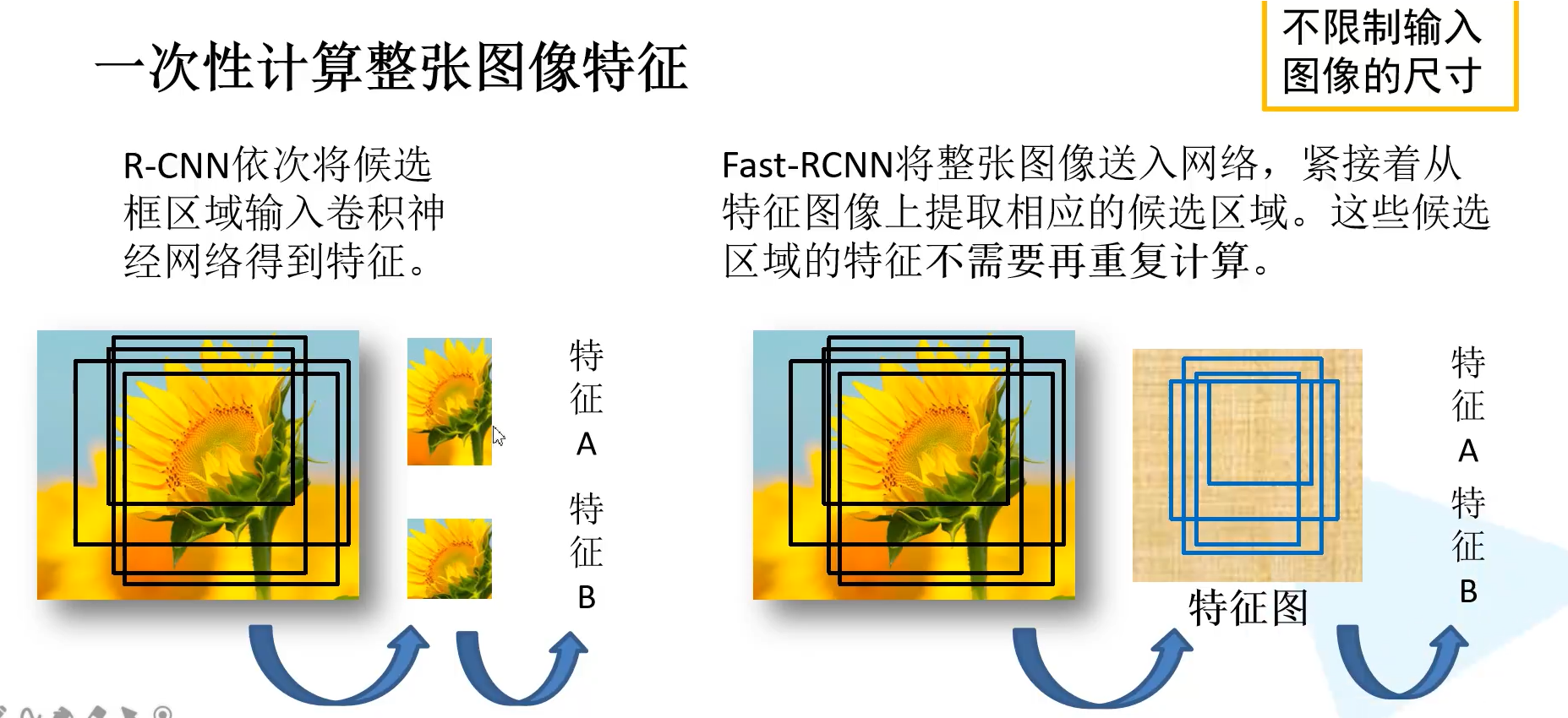
在这里插入图片描述
上图为R-CNN与Fast-RCNN生成候选区域的方式对比

R-CNN
可以看到R-CNN生成的候选框都需要输入深度网络提取特征，进行正向传播，冗余区域的重复计算，极大的增加了计算量，降低效率。
Fast-RCNN
它将整张图片输入网络，得到特征图，SS算法得到的候选框映射到特征图来获取特征，这样就不需要再重复计算这些候选区域。大大减小了计算量。

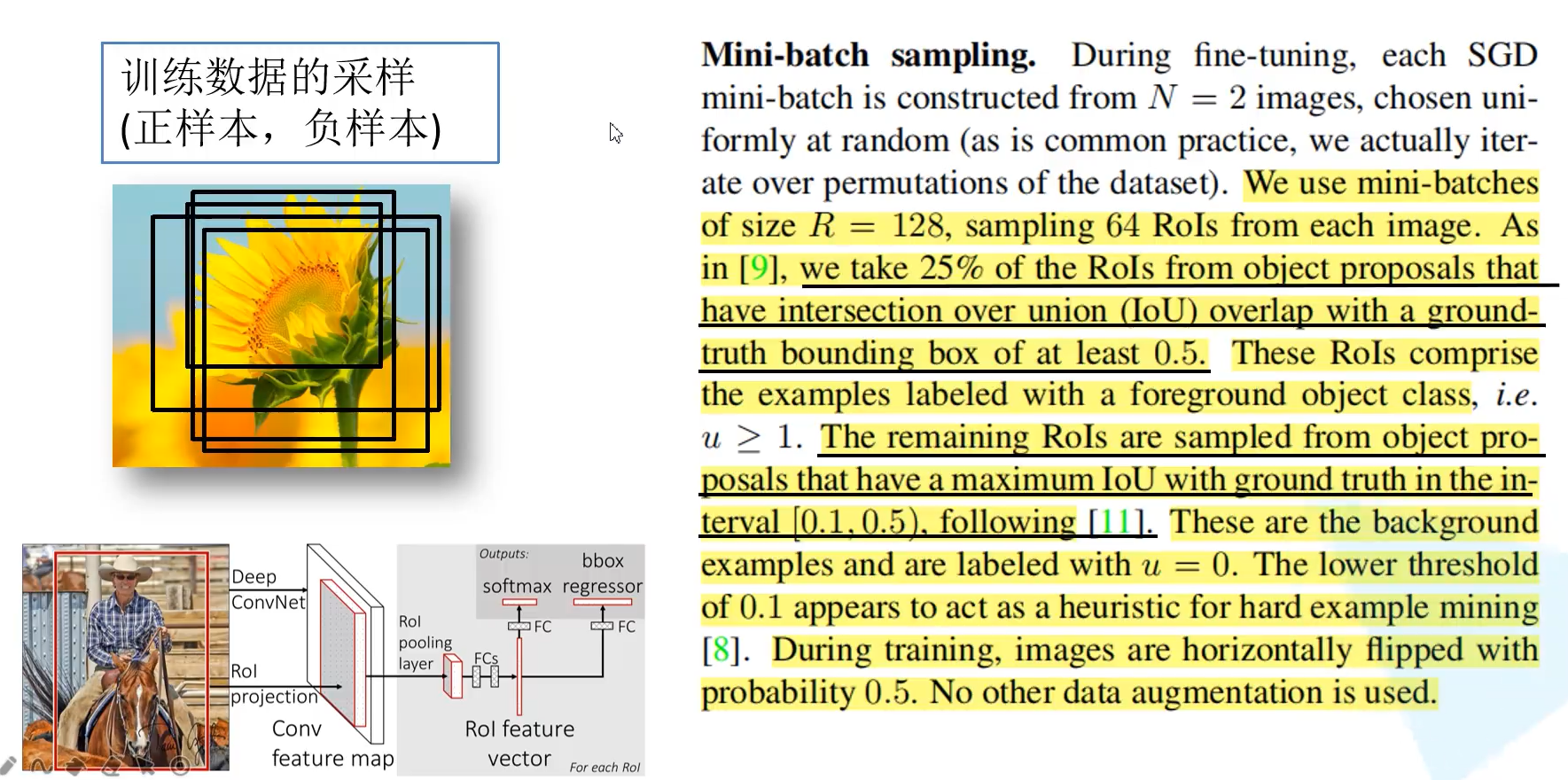
训练数据的采样（正样本与负样本）

与R-CNN不同的是，我们并没有使用SS算法生成的所有候选框，SS算法生成的近2000个候选框，实际上训练只使用了一小部分的候选框，而且样本分为正样本和负样本。具体论文里面有提到：分为正样本和负样本是为了平衡数据，因为如果正样本明显偏多，那么网络会理所当然的认为待识别的候选框是目标种类的一种，但实际上候选框也很有可能是背景，因此为了平衡包含目标和包含背景分为了正样本和负样本。

正样本与负样本的定义：候选框与真实框IOU大于0.5即为正样本，IOU在[0.1，0.5]，记为负样本。

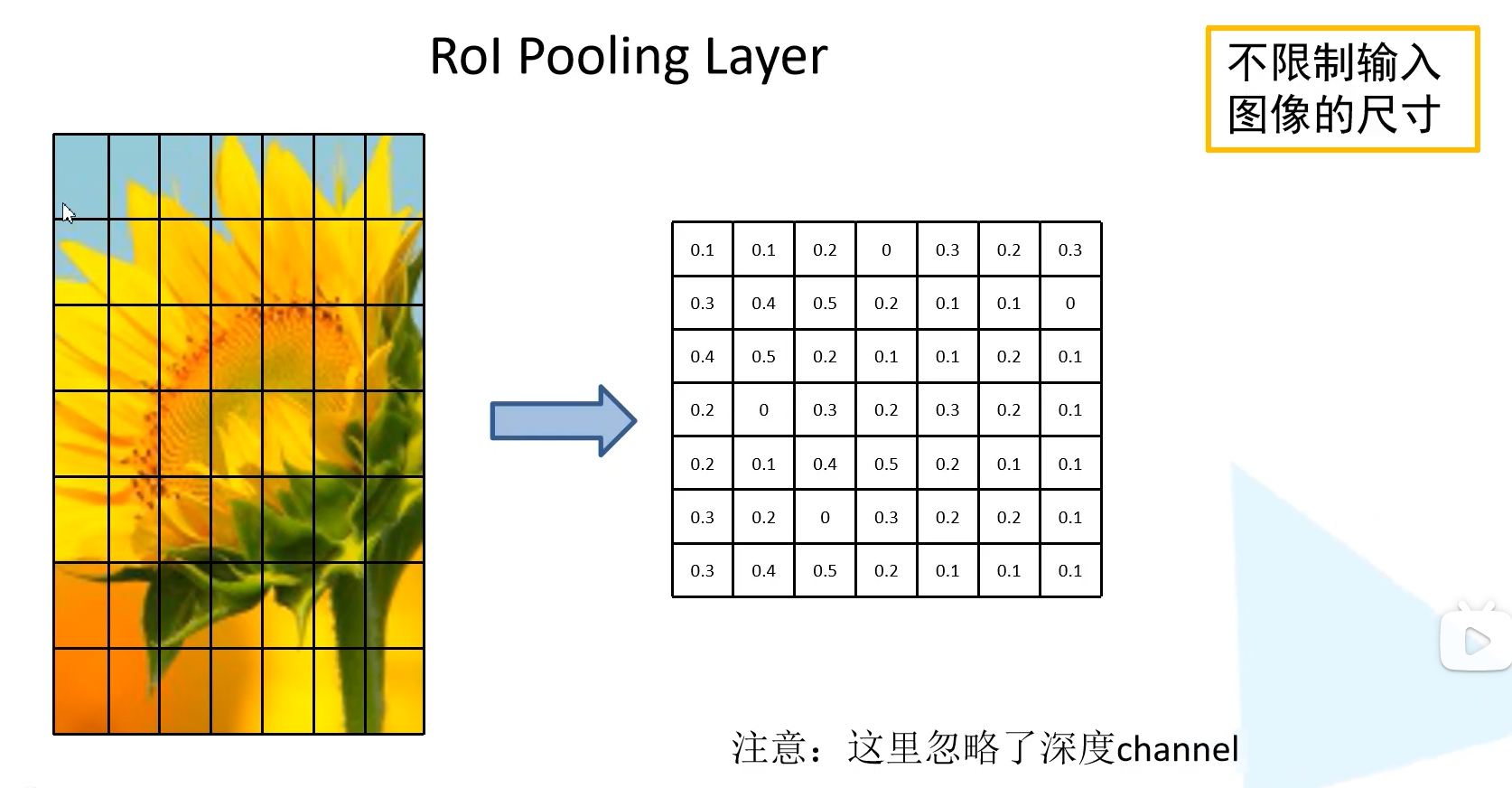
2.2.ROI Pooling层

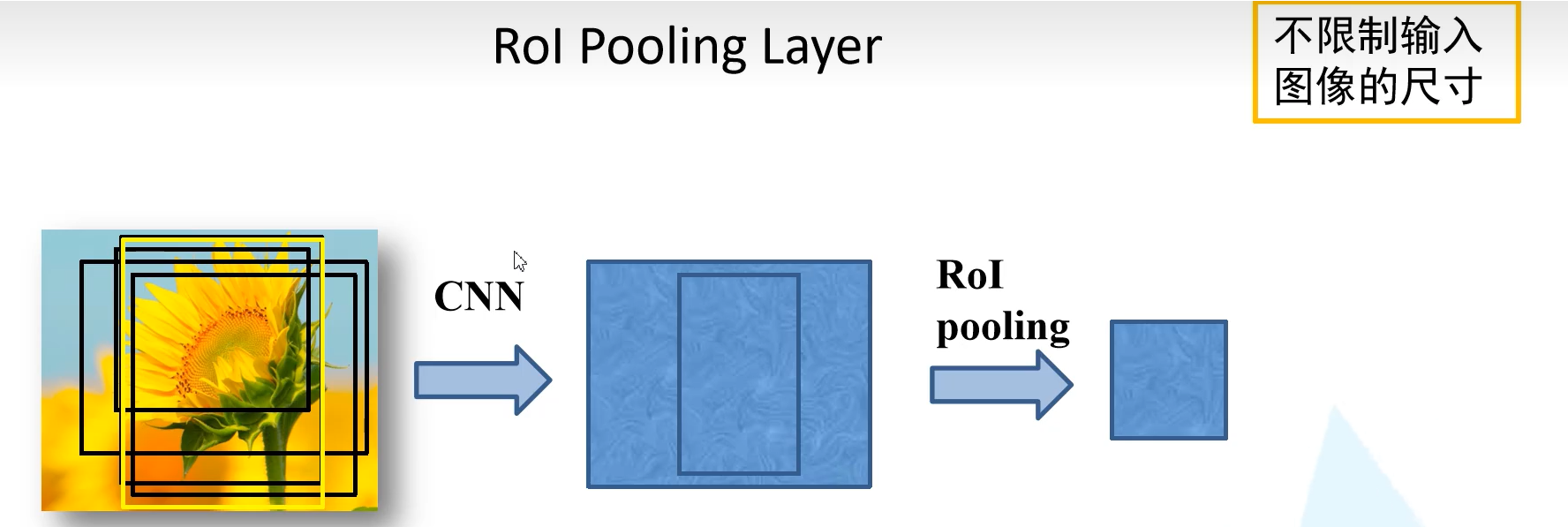
在这里插入图片描述

ROI Pooling层的实现

将样本划分为7*7个区域，对每个区域进行max pooling操作
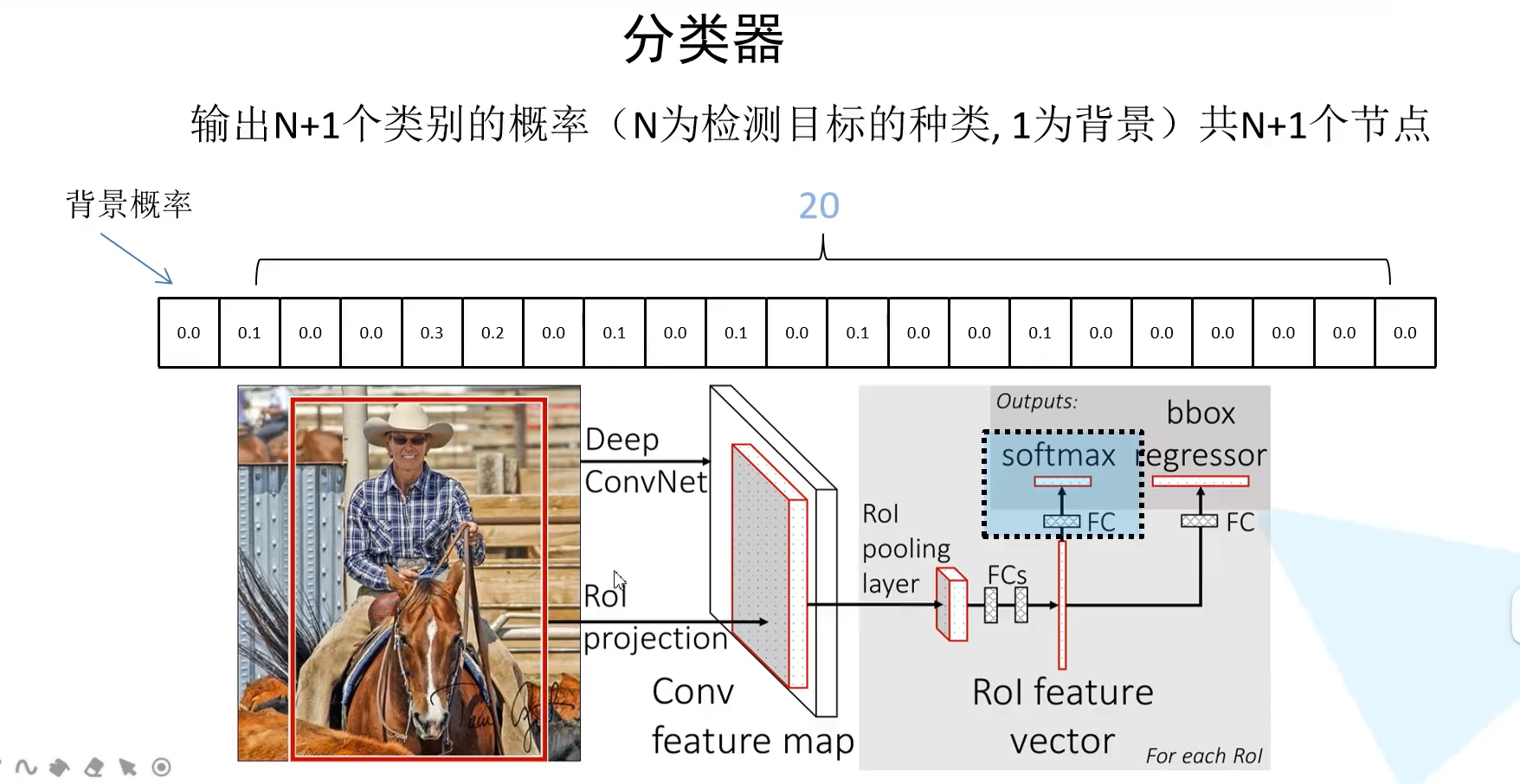
在这里插入图片描述

2.3.分类器

在这里插入图片描述
上面讲到我们在提取特征后经过ROI pooling层处理缩放到相同大小，然后拉直展平再经过两个全连接层，再分别于并联全连接层来分别进行类别概率的预测和bounding box边界框的预测。

对于分类器最后输出N+1个类别的概率，N为检测目标的类别数目，1为背景，得到的概率分布是经过了softmax的处理。

2.4.边界框的预测

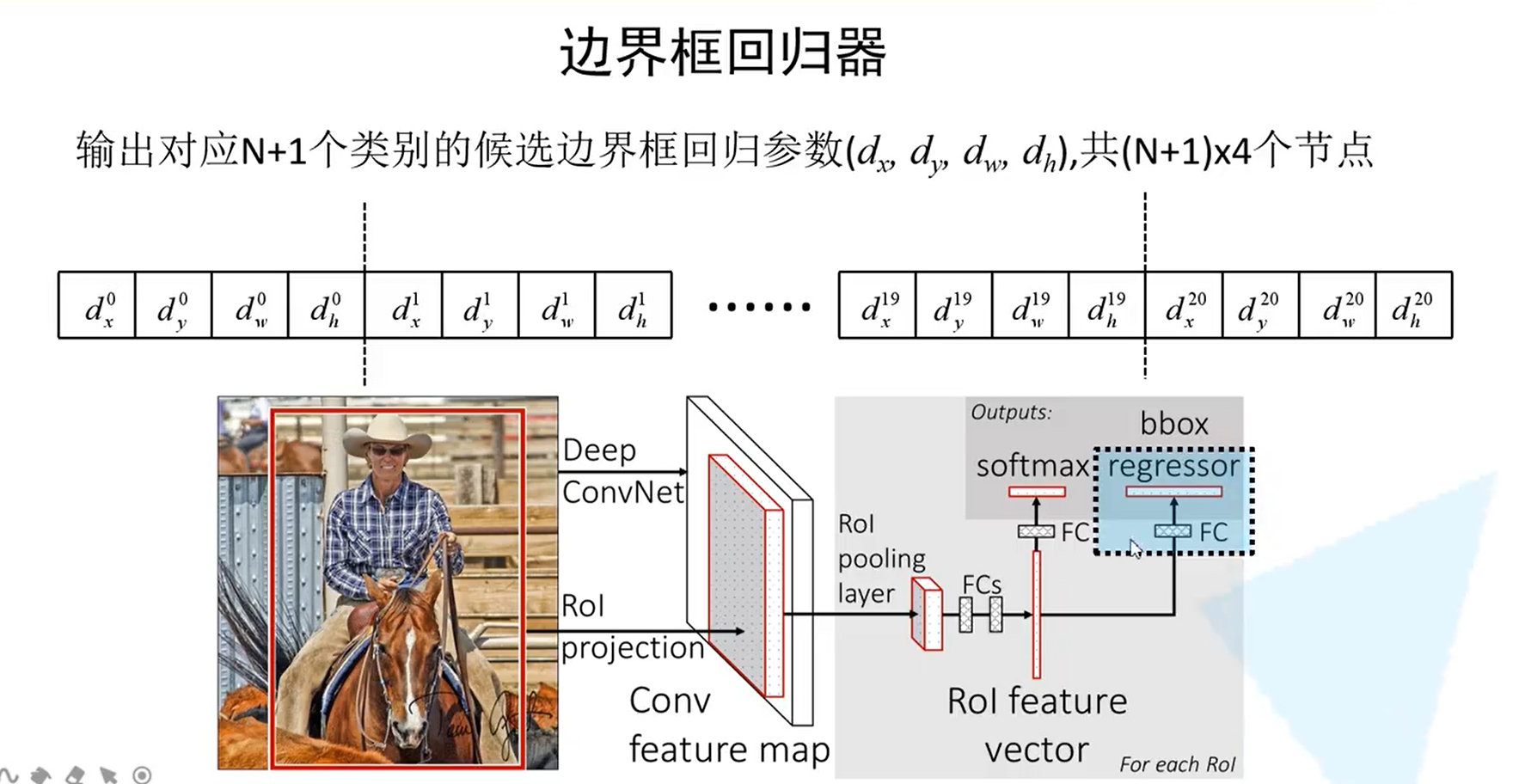
在这里插入图片描述
对于每个类别都会输出一组候选框回归参数(d_x, d_y, d_w, d_h)最后一层输出的结点个数为（N+1）*4

那么如何利用这些参数得到最终的预测框？
在这里插入图片描述

如图中所示：P表示预测框，G为真实框、G^为最终预测框，我们可以这么理解这几个公式：认为输出的回归参数对预测框进行中心坐标x,y的偏移调整，以及对候选框的宽和高进行缩放调整。

这几个公式来自于R-CNN论文，exp指指数次方。

2.5.损失计算

在这里插入图片描述
与R-CNN不同的是，Fast-RCNN因为分类与边界框的回归是一起训练的，因此损失也为对应部分损失的和。

2.5.1.分类损失

$L_{cls}(p, u)$ 指分类的损失，p为预测类别的概率分布p=p_0,p1,…pk,u为目标真实类别标签，计算公式为：

$L_{cls}(p, u) = -log^{p_u}$

Pu指当前框预测类别为u的概率。实际上上面的公式就是为交叉熵损失，只不过其他的类别标签为0，因此被化简了。
在这里插入图片描述

2.5.2.边界框回归损失

$\lambda表示平衡系数来使数值稳定$
[u>=1]为艾弗森括号，当真实标签为u类别这一项为1，当不满足这个条件等于0，也就是说只有预测类别不是背景才为1，为背景则为0, $t^u$ 为预测的边界框回归参数,具体为：
${t_x}^u,{t_y}^u,{t_w}^u,{t_h}^u)$
v为真实的边界框回归参数（v是通过真实的框位置中心和框宽和高利用上面的公式反推而来的，反推公式如下）