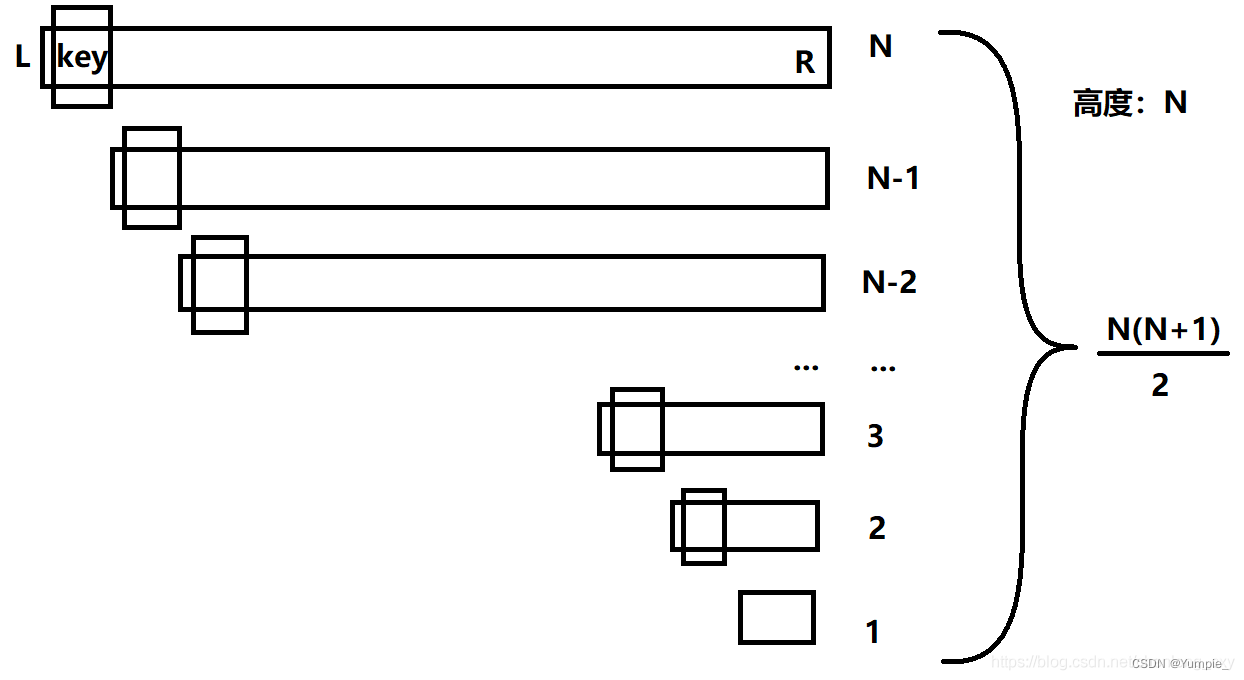
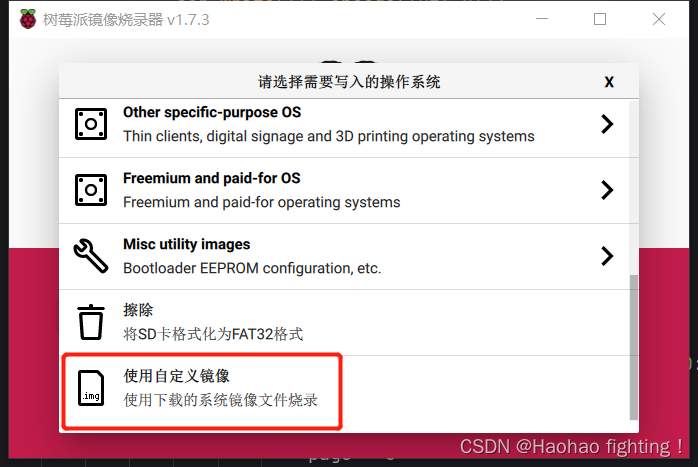
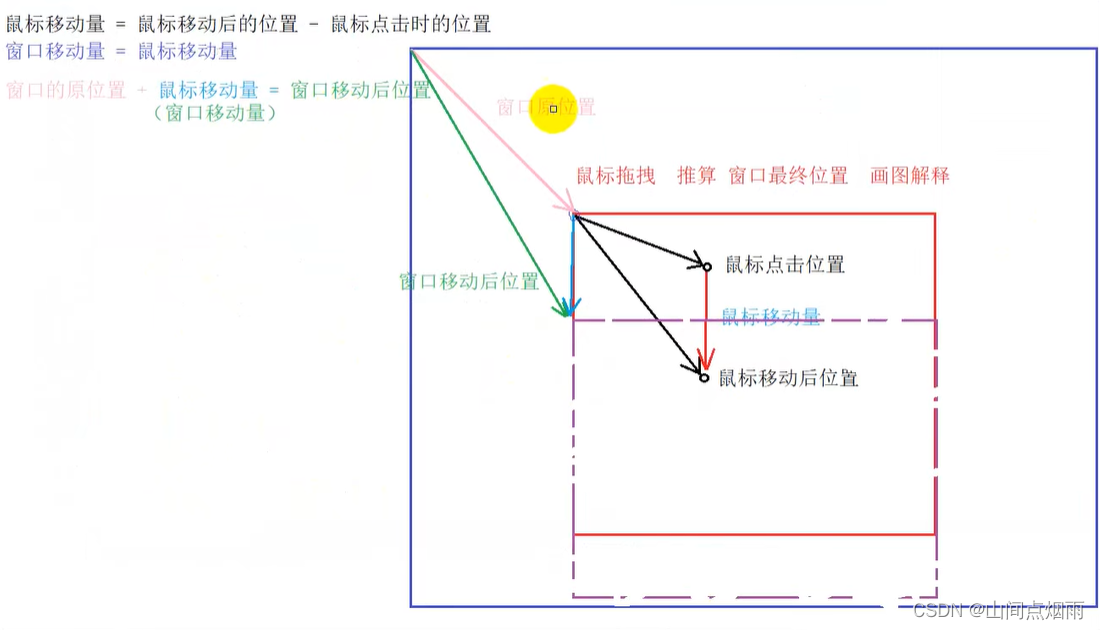
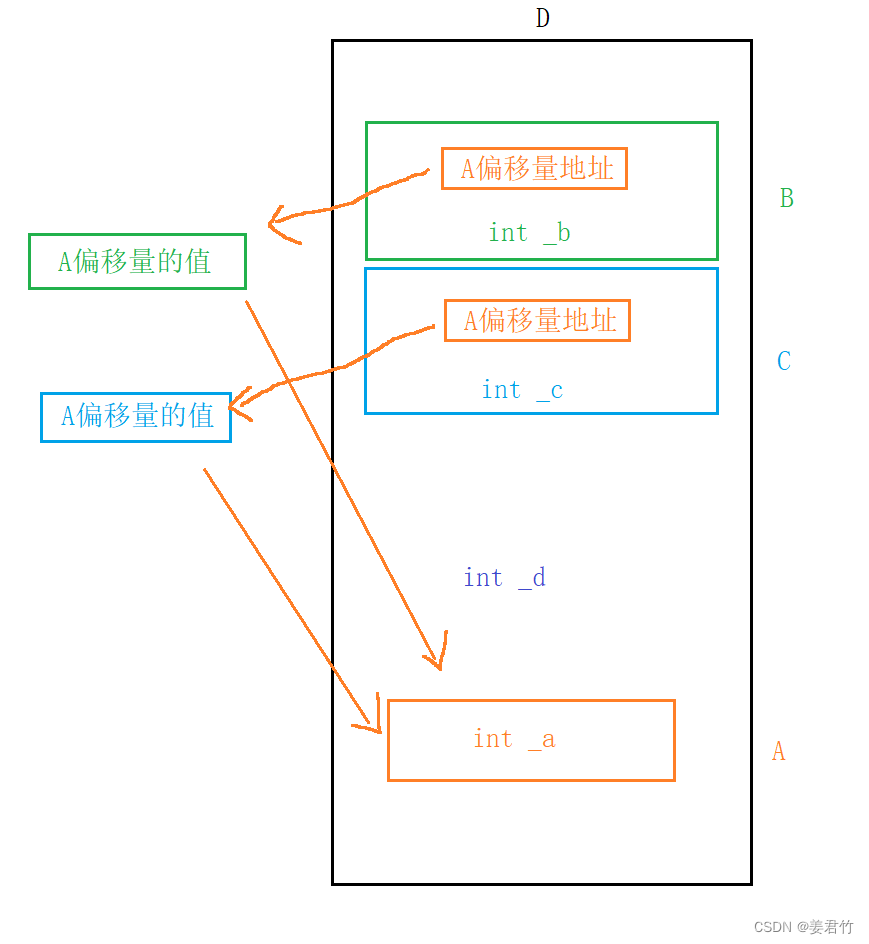
学习了strstr库函数后,老师让了解KMP算法,这也算是我接触到的第一个算法。
由于这一块得自己翻资料自学,因此初识比较吃力。
后面根据自己的理解方式,个人认为理解KMP算法最关键点就是理解next数组是怎么生成的。
下面说说我理解next的方法,有些简单粗暴。
首先,根据教程上的范例通过改造,直接将生成的next数组的所有元素打印出来。
然后再输入各种字符串,通过“实践”的方式通过观察规律来理解。
我们先不看代码,直接看运行结果:
我们用“ABCDABCE”来举例。
当字符串为“ABCDABCE”时,next数组是{-1,0,0,0,0,1,2,3,0}
下面用图示来理解。
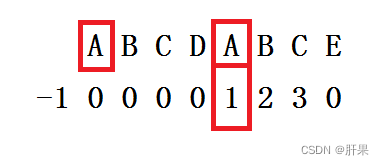
如上图所示,我们先找到next上第一个正数。
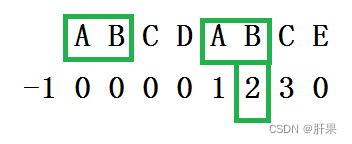
然后移动到后面的正数,以此类推。
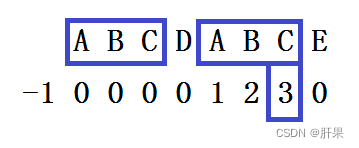
通过上面三幅图,有没有发现什么规律?
我们可以通过next数组元素中的数字n,观察到在字符串中第一个字符开始的n个字符,和这个数组元素对应位置的字符串向前n个数字是一样的。
我们再举一个更加极端一点的字符串:“AAAAAAAA”
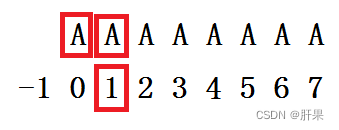
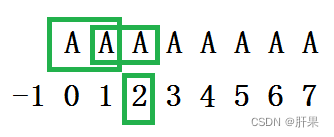

我们可以看到,如果按照前面的方式来画这种情况,似乎这里所有的数字都少了1个。这里是为什么呢?个人理解应该是前缀和后缀不能完全重叠。
我们再举个例子:“ABBBBBBB”
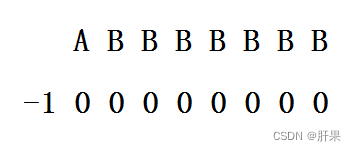
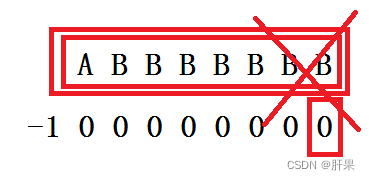
看到这里,我们可以理解为什么第二串字符串为什么不能根据第一串的方式去圈图。因为要是能圈上整个字符串,那无论什么字符串都能被圈上,这显然是不对的。
因此到这里,我们能够初步理解next数组的生成原理了。知道了原理,就能够更好的理解代码的实现方式了。生成next数组的代码如下:
#include <stdio.h>
void getNext(char* p, int* next) {
int len = strlen(p);
int i = 0, j = -1;
next[0] = -1;
while (i < len) {
if (j == -1 || p[i] == p[j]) {
++i;
++j;
next[i] = j;
}
else {
j = next[j];
}
}
}
int main() {
char p[] = "ABCDABCE";
int next[9];
int i = 0;
getNext(p, next);
for (i = 0; i < 9; i++)
{
printf("%d ", next[i]);//直接将next所有元素打印出来
}
printf("\n");
return 0;
}
KMP算法:
以下前缀加了ChatAI答的都是笔者问询ChatAI给出的答案,毕竟作为初学者的笔者还无法写出官方理论性强的文字,囧。ChatAI的回答可以供大家参考。
ChatAI答:
KMP算法是一种用于字符串匹配的高效算法,其核心思想是利用已知的部分匹配信息来减少匹配的次数。
具体来说,KMP算法通过预处理模式字符串,得到一个部分匹配表(Partial Match Table或称为Next数组),该表记录了在每个位置时,失配后应该跳到哪个位置继续匹配,从而减少了匹配的时间复杂度。
KMP算法的匹配过程如下:
-
对模式串p进行预处理,得到部分匹配表next数组;
-
从文本串s的第一个字符开始和模式串p进行匹配,假设当前已匹配的长度为i,模式串的指针为j;
-
如果s[i]和p[j]匹配,则令i++和j++,继续匹配下一个字符;
-
如果s[i]和p[j]不匹配,根据next数组,将模式串指针j跳到next[j]的位置继续匹配(即,将模式串向右移动j-next[j]个位置),直到模式串匹配到末尾,或者匹配成功。
KMP算法的时间复杂度是O(n),其中n是文本串的长度。预处理部分匹配表的时间复杂度是O(m),其中m是模式串的长度。
KMP算法在实际应用中,由于其高效性和简单实现,被广泛用于字符串匹配领域,例如文本编辑器、代码编辑器等等。
问:可以举个KMP算法的例子吗?用C语言
ChatAI答:
下面是一个使用C语言实现的KMP算法的例子,用于在文本串中查找模式串的位置。
#define _CRT_SECURE_NO_WARNINGS 1
#include <stdio.h>
#include <string.h>
void getNext(char* p, int* next) {
int len = strlen(p);
int i = 0, j = -1;
next[0] = -1;
while (i < len) {
if (j == -1 || p[i] == p[j]) {
++i;
++j;
next[i] = j;
}
else {
j = next[j];
}
}
}
int kmp(char* s, char* p, int* next) {
int slen = strlen(s);
int plen = strlen(p);
int i = 0, j = 0;
while (i < slen && j < plen) {
if (j == -1 || s[i] == p[j]) {
++i;
++j;
}
else {
j = next[j];
}
}
if (j == plen) {
return i - j;
}
else {
return -1;
}
}
int main() {
char s[] = "ABCDABCABCDABCDABCE";
char p[] = "ABCDABCE";
int next[10];
getNext(p, next);
int pos = kmp(s, p, next);
if (pos != -1) {
printf("在位置%d匹配上了\n", pos);
}
else {
printf("没有匹配\n");
}
return 0;
}
在这个例子中,我们用kmp函数实现了KMP算法的主要逻辑。首先对模式串进行预处理,得到部分匹配表next数组。然后,使用i和j两个指针分别遍历文本串和模式串,进行匹配。如果匹配成功,则i和j都向后移动一位,否则根据next数组更新模式串的指针j。最后,如果匹配成功则返回模式串在文本串中的起始位置,否则返回-1表示模式串不在文本串中。
在本例中,s和p分别代表文本串和模式串,其输出结果应该是"在位置11匹配上了",表示模式串在文本串中的起始位置是第11个字符。
如果因为ChatAI回答得字数太多看得想犯困,那么我们还是通过简单图示来分析吧,就用上面的例子:
程序开始前,初始化之后如下图所示:


显然,在前面7个字符,s[i],p[j]都是一样的,都执行了绿色矩形框里的代码。但是,当i=7,j=7的时候,因为s[7]!=s[7],很遗憾,只能执行红色矩形框里的代码了。(j说:明明差一点点就能成功了……)
j=next[7],next[7]的值是3,因此j从7变成了3.
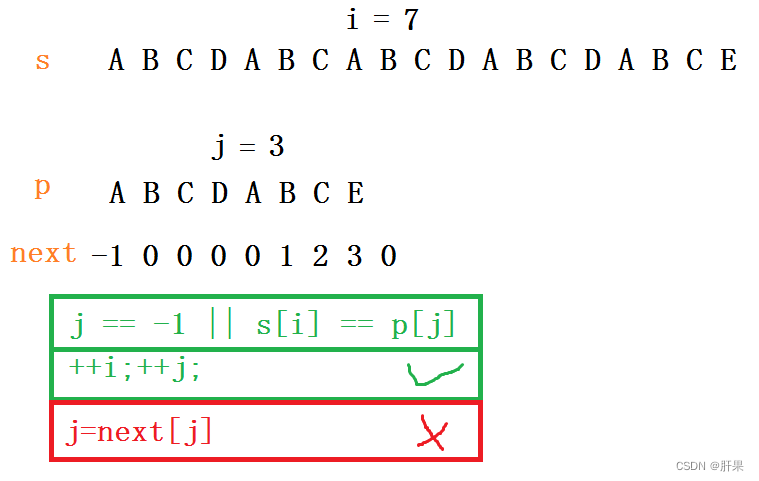
从这里就可以看出KMP和strstr的区别。如果是库函数strstr,此时i会回退到1,j也会回退到0重新开始匹配,而在这个例子的KMP算法中则省去了很多不必要的步骤。
当i=7,j=3时,s[7]!=p[3]还是执行的红色矩形框中的代码,因此j=next[3],j从3变成0

我发现,s[7]==p[0],因此执行绿色矩形框的代码,i和j同时+1

又是似曾相识的感觉,当i=14,j=7时,因为s[14]!=p[7],再次执行红色矩形框里的代码,j从7变成3.

但是这一次,神奇的事情发生了!
s[14]==p[3],他们都是’D’!
这一次j没有变成0,而是作为3重新执行绿色代码!

这一次,当j再一次到7的时候,终于没有被打回3,而是执行绿色矩形框代码顺利的变成了8,至此跳出循环。

因为跳出循环后,j等于8,因此返回了18-7=11。
而实际上,s确实在第11的位置开始,包含了整p.
通过感知这个例子,明显能够感觉到KMP算法在时间复杂度上比strstr简单了很多。
其他咨询ChatAI的问题:
问:next[]中的数字代表什么意思?
ChatAI答:
在KMP算法中,next[]数组是用来保存“最长的相等的前缀后缀长度”的数组。举个例子,如果模式串的某一位置i之前的字符串为"abab",那么next[i]就表示“abab”的最长相等前缀后缀的长度。也就是说,next[i]存储的是模式串中,第i个字符之前的子串中最长公共前后缀的长度。
利用next[]数组,KMP算法能够避免在匹配过程中对已经匹配过的部分进行重复匹配,从而提高算法的效率。当匹配失败时,我们可以通过next数组中存储的最长公共前后缀的长度,将模式串向右移动对应的位数,从而继续进行匹配。这就是KMP算法的关键思想。
因此,next[]数组实际上是KMP算法中非常重要的一部分,通过保存最长相等的前缀后缀长度,能够使得算法实现方便而有效地完成字符串匹配。