线性回归实现原理

news2024/10/1 19:35:55

一.定义
回归是监督学习的一个重要问题，回归用于预测输入变量和输出变量之间的关系，特别是当输入变量的值发生变化时，输出变量的值也随之发生变化。回归模型正是表示从输入变量到输出变量之间映射的函数

回归的目的是预测数组型的目标值。

线性回归：根据已知的数据集，通过梯度下降的方法来训练线性回归模型的参数w，从而用线性回归模型来预测数据的未知的类别。

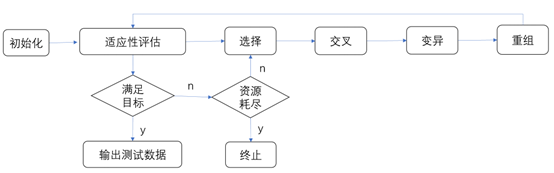
二.学习过程

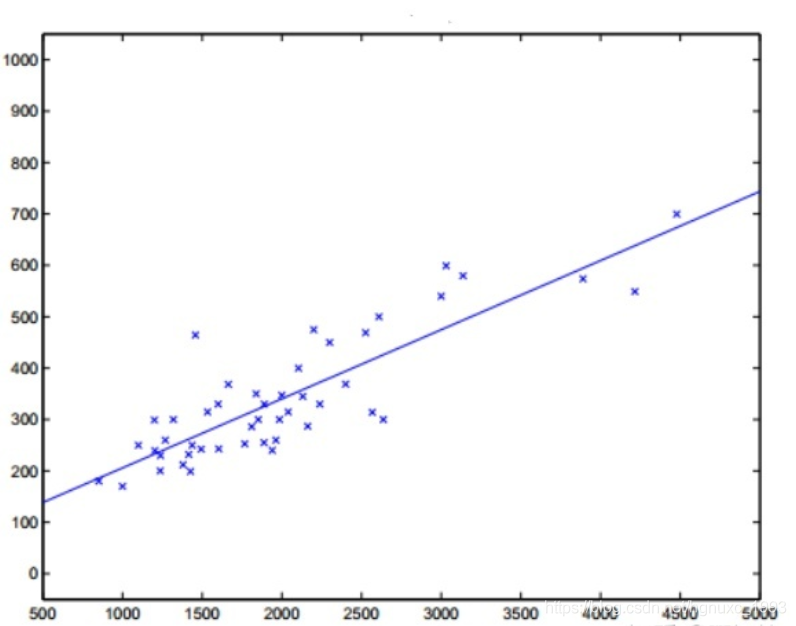
三.损失函数

使用均方误差作为损失函数；使用均方误差的原因：有十分好的几何意义，对应了常用的欧式距离。在线性回归中，就是找到一个直线，使得所有样本到直线的欧式距离最小。

损失函数：

求导过程如下：

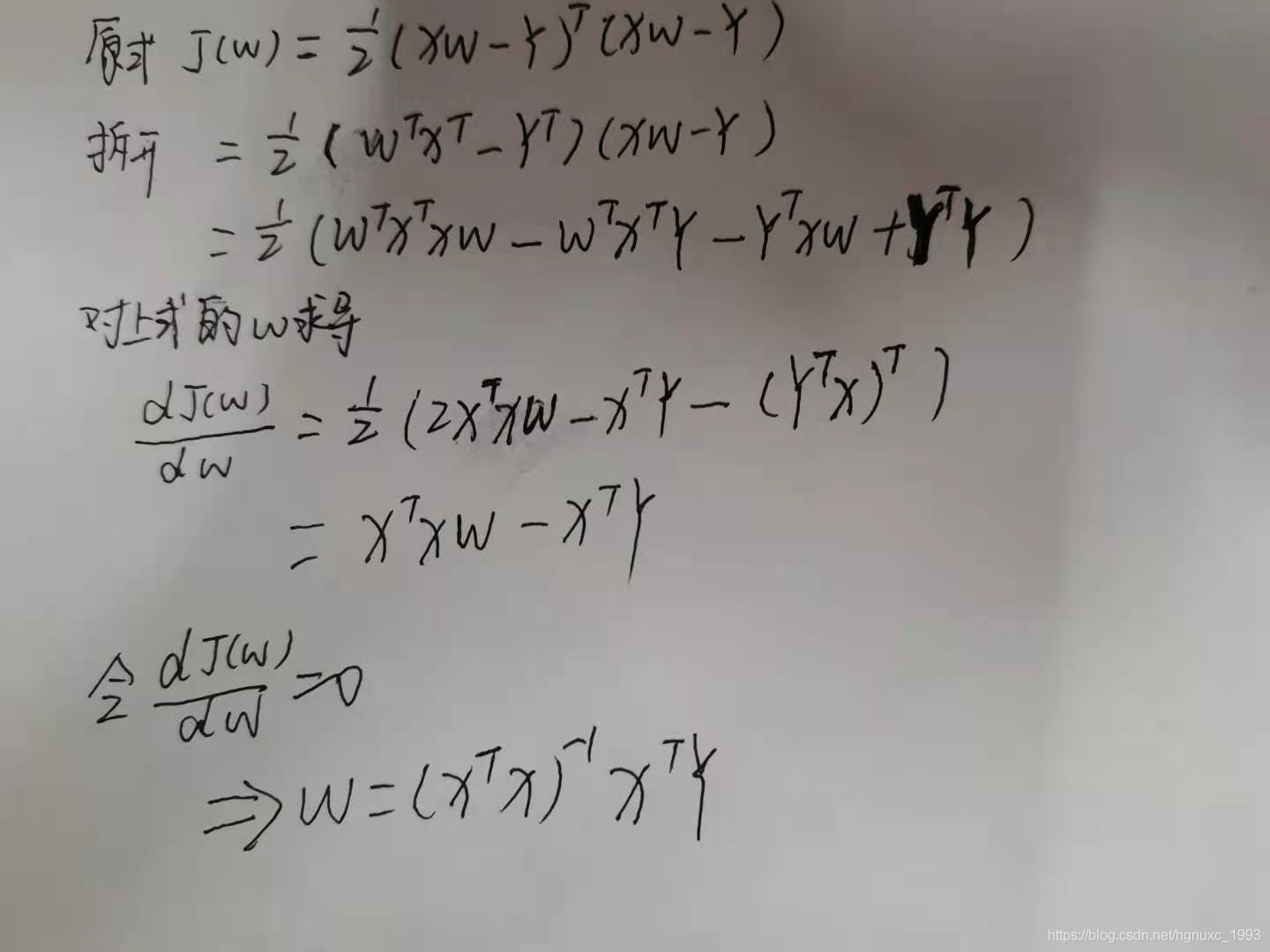
上式最小二乘法求导用到的数学公式：

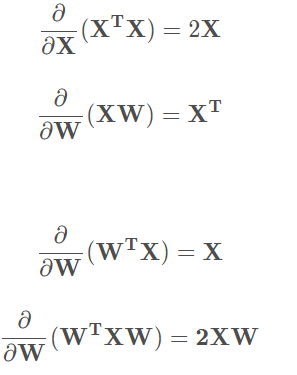
①当 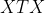$XTX$ 为满秩矩阵或者正定矩阵时，可使用正规方程法，直接求得闭式解。

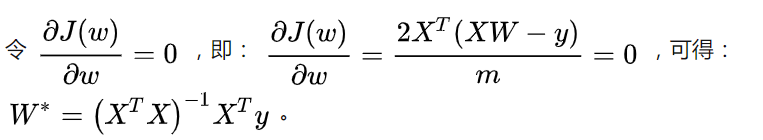
可直接用最小二乘法得出模型的参数w

算法实现：（Python）：

def Regres(X，Y):
    x = mat(X); y = mat(Y).T
    if linalg.det(x.T*x) == 0.0:#判断行列式是否为0
        print ("矩阵行列式为0，不可逆")
        return 0
    else return ((x.T*x).I * (x.T*y))#返回为已经求出的w，其中I为求逆操作

②当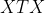 $XTX$ 为不可逆矩阵时，可使用梯度下降的方法

损失函数：

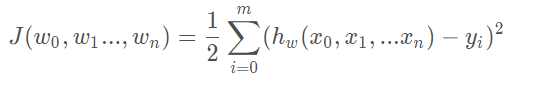
使用矩阵表示（方便计算）

E=h-y

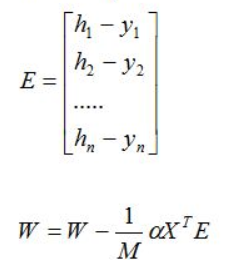
四.优缺点
优点：结果易于理解，计算不复杂

缺点：对非线性的数据拟合不好，不能处理非线性模型

五.应用场景
线性回归预测PM2.5预测
给定训练集train.csv，要求根据前9个小时的空气监测情况预测第10个小时的PM2.5含量。

训练集介绍：

　　(1)：csv文件，本次作业使用丰原站的观测记录，分成 train set 跟 test set，train set 是丰原站每个月的前 20 天所有资料。test set 则是从丰原站剩下的资料中取样出来。(取每个月前20天的数据做训练集，12月X20天=240天，每月后10天数据test set 用于测试，对学生不可见); （2）：test.csv : 从剩下的资料当中取样出连续的 10 小时为一笔，前九小时的所有观测数据当作 feature，第十小时的 PM2.5 当作 answer。一共取出 240 笔不重複的 test data，请根据 feature 预测这 240 笔的 PM2.5。

　　(3)：每天的监测时间点为0时，1时......到23时，共24个时间节点;

　　(4)：每天的检测指标包括CO、NO、PM2.5、PM10等气体浓度，是否降雨、刮风等气象信息，共计18项；

(5):数据集https://github.com/datawhalechina/leeml-notes/blob/master/docs/Homework/HW_1/Dataset

数据处理

【下文中提到的“数据帧”并非指pandas库中的数据结构DataFrame,而是指一个二维的数据包】

根据作业要求可知，需要用到连续9个时间点的气象观测数据，来预测第10个时间点的PM2.5含量。针对每一天来说，其包含的信息维度为(18,24)(18项指标，24个时间节点)。可以将0到8时的数据截

取出来，形成一个维度为(18,9)的数据帧，作为训练数据，将9时的PM2.5含量取出来，作为该训练数据对应的label；同理可取1到9时的数据作为训练用的数据帧，10时的PM2.5含量作为label......以此

分割，可将每天的信息分割为15个shape为(18,9)的数据帧和与之对应的15个label。

下面时train.csv训练集数据的内容：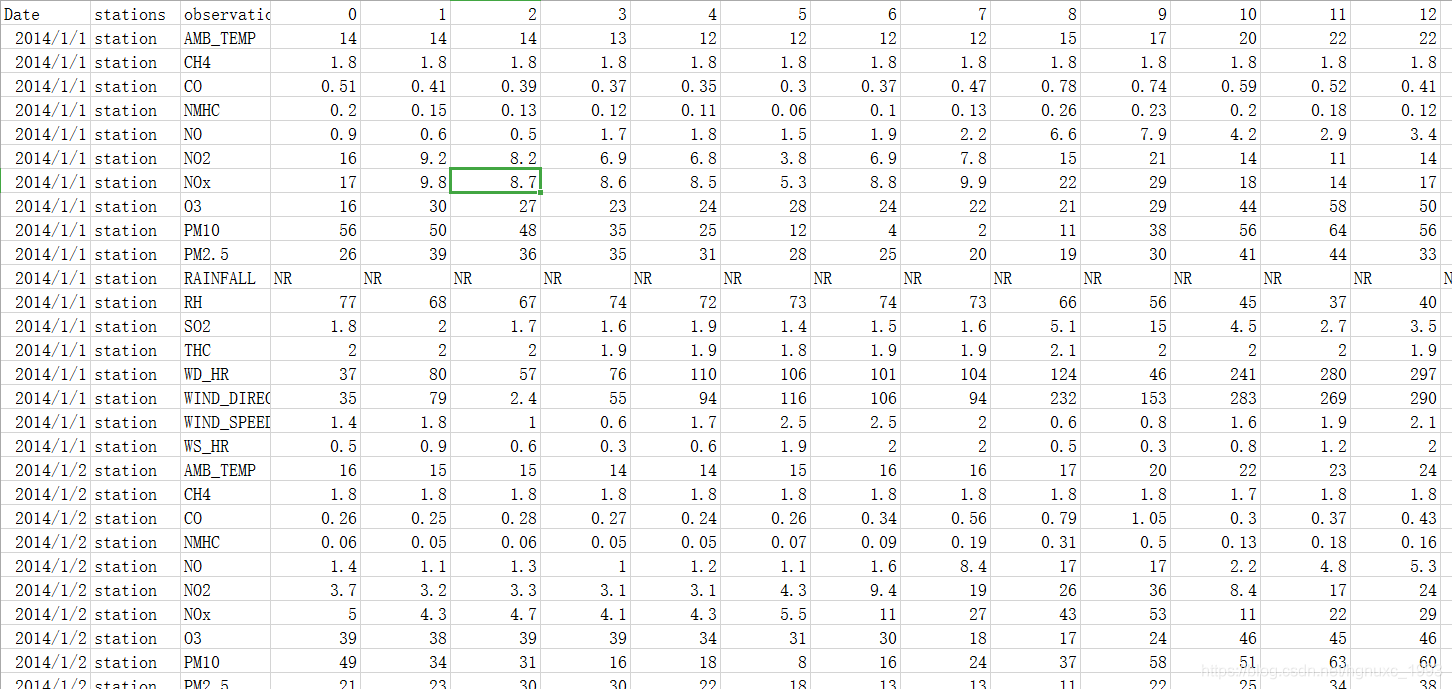

源码：

import numpy as np
import pandas as pd
df =pd.read_csv('work/hw1_data/train.csv',encoding='big5')
print(df)
df.drop(["日期","測站"],axis=1,inplace=True)
print(df)
col=df["測項"].unique()
#print(col)
new_train=pd.DataFrame(np.zeros([18,24*240]),index=col)
#print(new_train)
for i in col:
    df1=df[df["測項"]==i]
    df1.drop(["測項"],axis=1,inplace=True)
    df1=np.array(df1)  #数组
    #print(df1)
    df1[df1=="NR"]="0"  #将数组中nr的值成0
    df1=df1.astype("float")
    df1=df1.reshape(1,5760)
    #print(">>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>")
    new_train.loc[i]=df1  #形成整行插入一维数组，也可以转化成整列插入，设置new_train为（24*240,18），则new—train[i]=df1
print(new_train)
 
#接下来提取训练集的标签
label=np.array(new_train.loc["PM2.5",9:],dtype='float32')   #提取训练集的标签
label=label.reshape(5751,1)   #构成5751*1的列矩阵
print(label)
 
#接下来训练模型，得出w
label=label.astype("float")  #数组所有的值转化成float型，标签
#print(label)
m=len(label)
#print(m)
eta=0.00001
w=np.ones((10,1))
for t in range(100):
    for v in range(m):
        x=np.array(new_train.loc["PM2.5",v:v+8])  #样本的所有特征值
        x=np.insert(x,0,1.0)  #在9个特征值前加一个1.0,方便处理偏置b
        h=np.dot(x,w)
        err=label[v]-h  #第一次更新label-wx
        x=x.reshape(10,1)  #装置x变成10*1
        w+=eta*x*err  #每次变更w向量
print(w)
 
#接下来提取测试集的标签，并预测
df2=pd.read_csv('work/hw1_data/test.csv',encoding='big5')  #提取测试集的特征值，接下来预测
#print(df2)
test=df2.iloc[:,2:]
test=np.array(test)
test[test=="NR"]="0"   #替换非数字的字符
test=test.astype("float")  #转化成数值
print(test)
print(test.shape)
t=9
test1=[]
for i in range(240):  #提取240个测试集
    test1.append([1.0,*test[t]])
    #print(test1)
    t=t+18
#print(test1)
test1=np.array(test1)  #将测试集变成数组
print(test1.shape)  #打印数组shape
t_label=[]
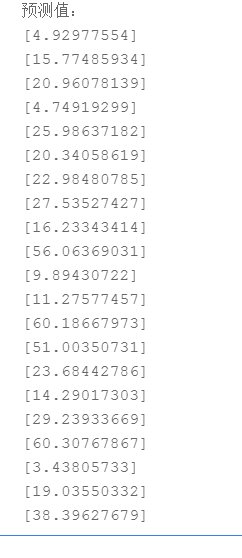
print("预测值：")
for k in range (240):  #遍历测试集
    test_label=np.dot(test1[k],w)
    print(test_label)
    t_label.append(test_label)
#t_label=np.array(t_label)  #转化成一维数组
#t_label=t_label.reshape(240,1) #转化成240*1的列数组
#print(t_label)#打印列数组

运行结果：