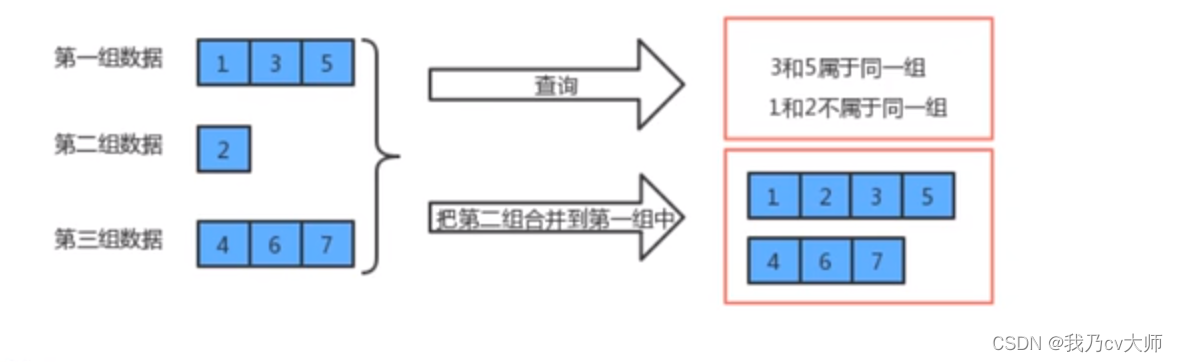
并查集是一种树型的数据结构，并查集可以高效地进行如下操作：

1、查询元素p和元素q是否属于同一组

2、合并元素p和元素q所在地组

 并查集结构：

是一种树型结构，这棵树地要求比较简单

1、每个元素都唯一对应一个节点

2、每一组数据中地多个元素都在同一棵树内

3、一个组中的数据对应的树和另外一个组中的数据对应的树之间没有任何联系

4、元素在树中没有子父级关系的硬性要求

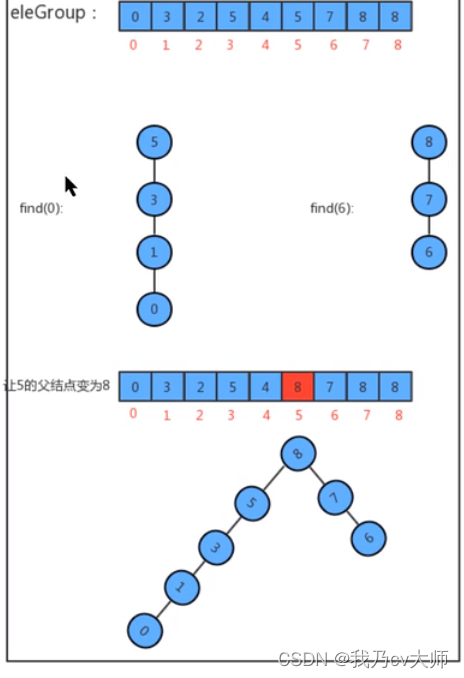
 并查集的查找思路：

在数组中寻找，根据下标找到对应的元素，该元素如若不等于下标，则为该下标的父节点。当下标值等于对应下标元素的值，便是找到所要查找元素分组的标识符，思路图如下所示

 并查集的合并思路：

找到p,q的根节点，让p所在树的根节点的父节点为q的根节点即可：

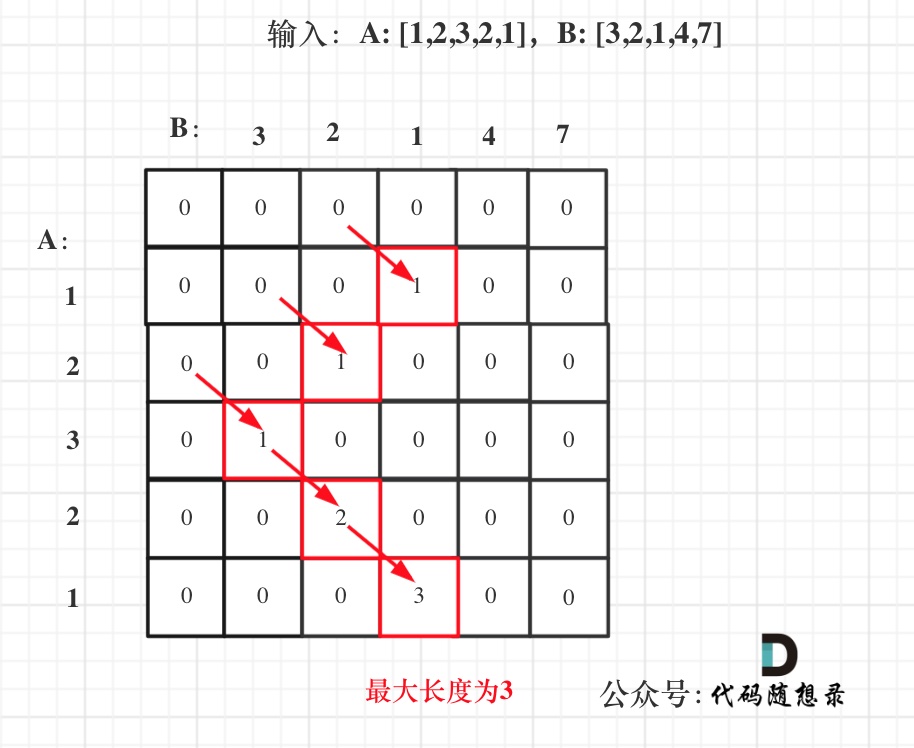
 并查集的路径压缩优化（以上方法可能会生成线性树，使得查找的最大时间复杂度为On)，为了降低查找的时间复杂度，

提高find的效率，我们可以在合并的时候，将小树合并到大树中，最大程度降低树的深度。

 

 最终并查集的代码结构如下所示

   public class UF{
        //记录节点元素和该元素所在分组的标识
        private int[] eleAndGroup;
        //记录并查集中数据的分组个数
        private int count;
        //用来存储每一个根节点对应树中保存的节点的个数
        private int[]sz;
        //初始化并查集
        public UF(int N){
            this.count=N;
            this.eleAndGroup=new int[N];
            for (int i = 0; i < eleAndGroup.length; i++) {
                eleAndGroup[i]=i;
            }
            this.sz=new int[N];
            //默认情况下，sz每个索引处的值都是1
            for(int i=0;i<sz.length;i++){
                sz[i]=1;
            }
        }
        //获取当前并查集中的数据有多少个分组
        public int count(){
            return count;
        }
        //元素p所在分组的标识符
        public int find(int p){
            while (true){
                if(p==eleAndGroup[p]){
                    return p;
                }
                p=eleAndGroup[p];
            }
        }
        //判断并查集中元素p和元素q是否在同一分组中
        public boolean connected(int p,int q){
            return find(p)==find(q);
        }
        //把p元素所在分组和q元素所在分组合并
        public void union(int p,int q){
            int proot=find(p);
            int qroot=find(q);
            //判断p和q是否已经在同一分组中
            if(proot==qroot){
             return;
            }
           //比较两棵树的大小
            if(sz[proot]<sz[qroot]){
                eleAndGroup[proot]=qroot;
                sz[qroot]+=sz[proot];
            }
            else {
                eleAndGroup[qroot]=proot;
                sz[proot]=sz[qroot];
            }
            //分组个数减1
            this.count--;
        }
    }