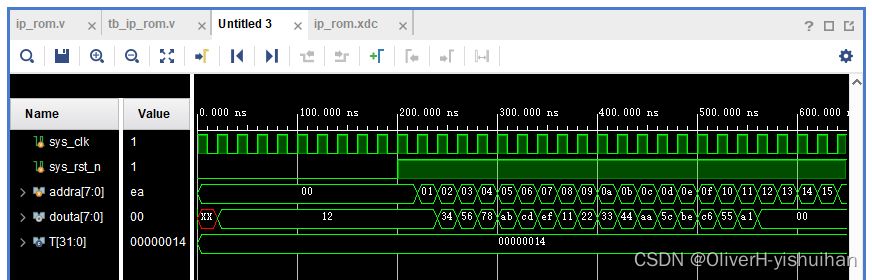
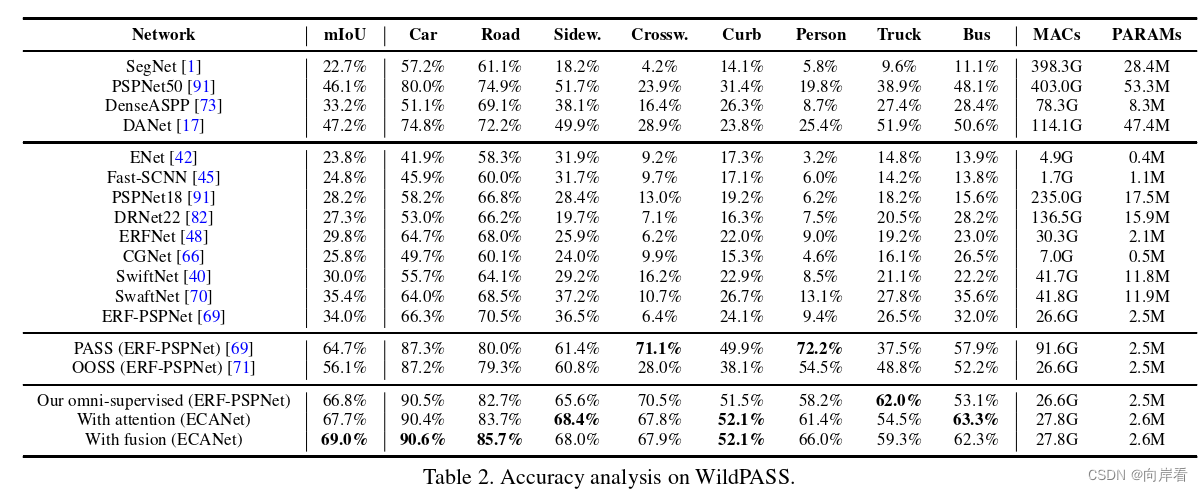
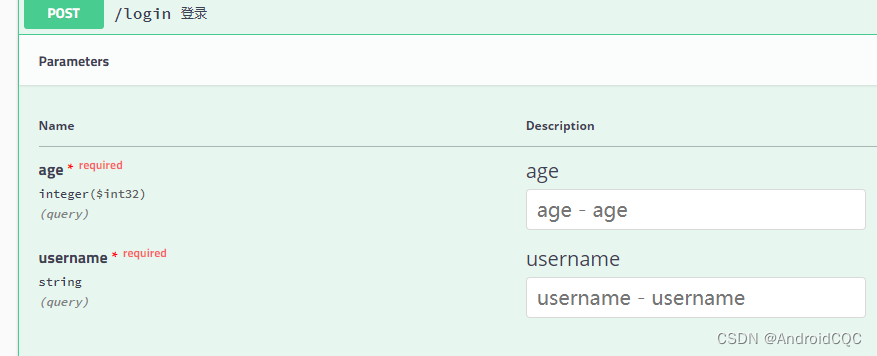
例:计算模式串"abaabcac"的KMP算法中next函数值
由函数定义
n
e
x
t
[
j
]
=
{
0
,
j
=
1
M
a
x
{
k
∣
1
<
k
<
j
且
"
t
1
t
2
⋅
⋅
⋅
t
k
−
1
"
=
"
t
j
−
k
+
1
t
j
−
k
+
2
⋅
⋅
⋅
t
j
−
1
"
}
1
,
k
=
1
next[j]=\left\{ \begin{aligned} 0 , & \ j=1 \\ Max & \{k|1<k<j且"t_1t_2···t_{k-1}"="t_{j-k+1}t_{j-k+2}···t_{j-1}" \} \\ 1 , & \ k=1 \end{aligned} \right.
next[j]=⎩
⎨
⎧0,Max1, j=1{k∣1<k<j且"t1t2⋅⋅⋅tk−1"="tj−k+1tj−k+2⋅⋅⋅tj−1"} k=1
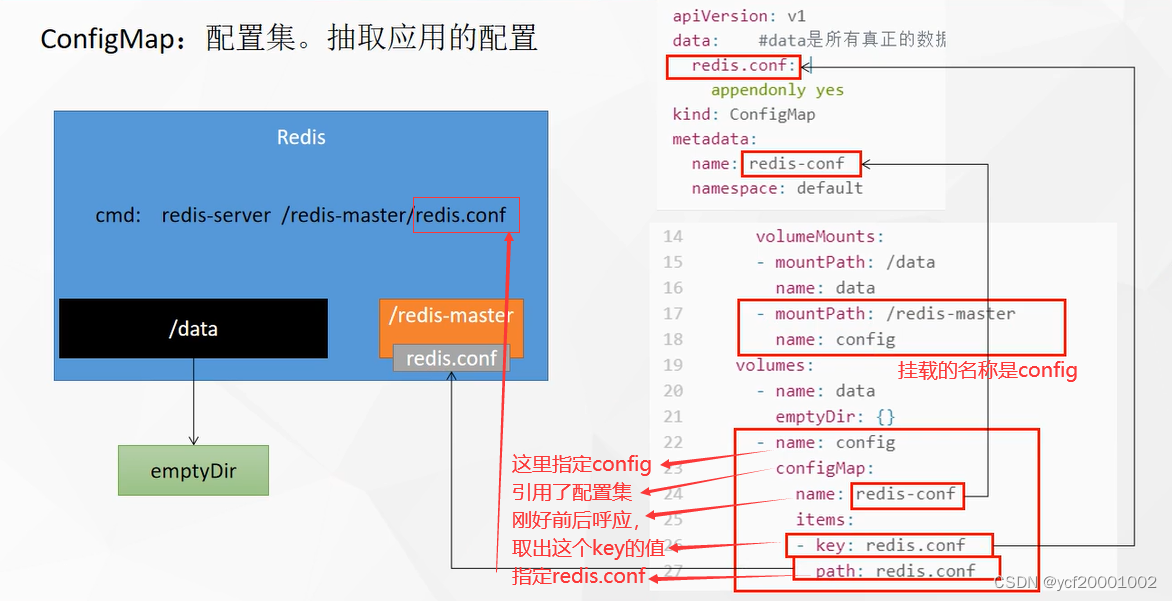
可得 next[1] = 0,其修正值 nextval[1] = 0
对模式串进行自我匹配的过程如图所示:(主串指针为i,子串指针为j)

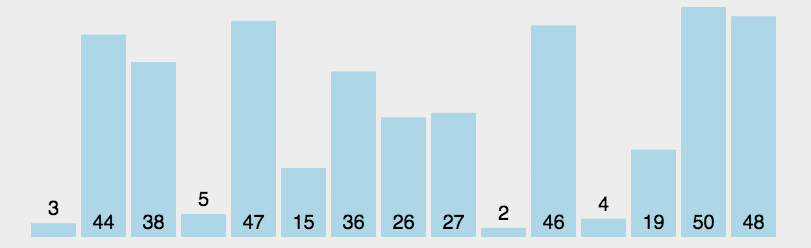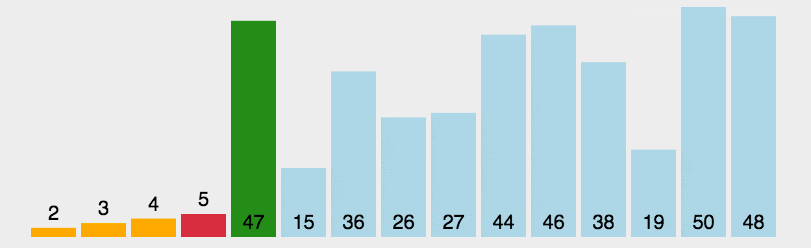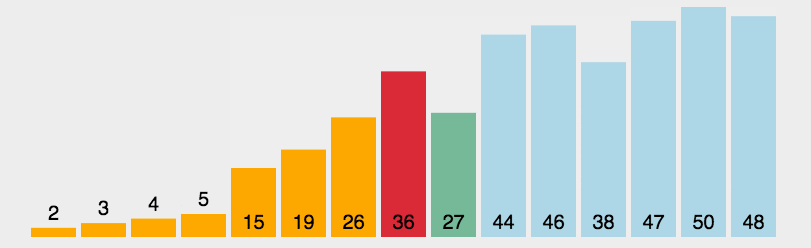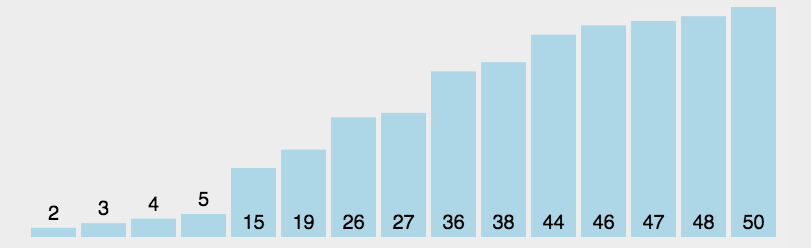
故计算得到的函数值为:
| 模式串 | a | b | a | a | b | c | a | c |
|---|---|---|---|---|---|---|---|---|
j | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
next[j] | 0 | 1 | 1 | 2 | 2 | 3 | 1 | 2 |
nextval[j] | 0 | 1 | 0 | 2 | 0 | 3 | 0 | 2 |