文章目录

1. 最长递增子序列【中等】
- 1.1 题目描述
- 1.2 解题思路
- 1.3 代码实现
2. 接雨水【困难】
- 2.1 题目描述
- 2.2 解题思路
- 2.3 代码实现
3. 二叉树中的最大路径和【困难】
- 3.1 题目描述
- 3.2 解题思路
- 3.3 代码实现
4. 二叉树的中序遍历【简单】
- 4.1 题目描述
- 4.2 解题思路
- 4.3 代码实现
5. 删除链表的倒数第 N 个结点【中等】
- 5.1 题目描述
- 5.2 解题思路
- 5.3 代码实现

1. 最长递增子序列【中等】

题目链接：https://leetcode.cn/problems/longest-increasing-subsequence/
参考题解：https://leetcode.cn/problems/longest-increasing-subsequence/solution/zui-chang-shang-sheng-zi-xu-lie-by-leetcode-soluti/

1.1 题目描述

给你一个整数数组 nums ，找到其中最长严格递增子序列的长度。

子序列 是由数组派生而来的序列，删除（或不删除）数组中的元素而不改变其余元素的顺序。例如，[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。

示例1：

输入：nums = [10,9,2,5,3,7,101,18]
输出：4
解释：最长递增子序列是 [2,3,7,101]，因此长度为 4 。

示例2：

输入：nums = [0,1,0,3,2,3]
输出：4

示例3：

输入：nums = [7,7,7,7,7,7,7]
输出：1

提示：

1 <= nums.length <= 2500
-10^4 <= nums[i] <= 10^4

进阶：

你能将算法的时间复杂度降低到 O(n log(n)) 吗?

1.2 解题思路

对于以数组某个位置 i 结束的最长递增子序列，一定是以前面各个位置结束的最长递增子序列加上 1 ，也就是加上当前位置，并且前面位置上的值要比当前位置 i 上的值要小。所以可以用双重循环实现，第一重循环遍历所有位置，找到以各个位置结束的最长递增子序列；第二重循环遍历在当前位置之前且比当前位置的值要小的位置，看以哪个位置结束的最长递增子序列加上 1 最大。用一个全局变量记录遍历过程中遇到的最大值，即为答案。

1.3 代码实现

class Solution {
public:
    int lengthOfLIS(vector<int>& nums) {
        int len = nums.size();
        vector<int> currentMaxLen(len, 1);
        int ans = 1;
        for(int i = 0; i < len; ++i) {
            for(int j = 0; j < i; ++j) {
                if(nums[j] < nums[i]) {
                    currentMaxLen[i] = max(currentMaxLen[i], currentMaxLen[j] + 1);
                    ans = max(ans, currentMaxLen[i]);
                }
            }
        }
        return ans;
    }
};

2. 接雨水【困难】

题目链接：https://leetcode.cn/problems/trapping-rain-water/
参考题解：https://leetcode.cn/problems/trapping-rain-water/solution/jie-yu-shui-by-leetcode-solution-tuvc/

2.1 题目描述

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

示例1：
在这里插入图片描述

输入：height = [0,1,0,2,1,0,1,3,2,1,2,1]
输出：6
解释：上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图，在这种情况下，可以接 6 个单位的雨水（蓝色部分表示雨水）。

示例2：

输入：height = [4,2,0,3,2,5]
输出：9

提示：

n == height.length
1 <= n <= 2 * 10^4
0 <= height[i] <= 10^5

2.2 解题思路

某个位置能够接到的雨水量，等于其左右两侧最高位置中的较小值减去该位置的高度。因此可以先扫描两遍，找到每个位置左右两侧的最高位置是多少，然后再扫描一次，计算各个位置能接的雨水量。一共是三次遍历循环。每个位置左/右两侧的最高位置是在其左/右相邻的前一个最高状态和自身高度之间选较大者，同时要注意边界条件的处理。

2.3 代码实现

class Solution {
public:
    int trap(vector<int>& height) {
        int len = height.size();
        vector<int> leftHighest(len, 0);
        vector<int> rightHighest(len, 0);
        leftHighest[0] = height[0];
        rightHighest[len - 1] = height[len - 1];
        for(int i = 1; i < len; ++i) {
            leftHighest[i] = max(leftHighest[i - 1], height[i]);
        }
        for(int i = len - 2; i >= 0; --i) {
            rightHighest[i] = max(rightHighest[i + 1], height[i]);
        }
        int ans = 0;
        for(int i = 0; i < len; ++i) {
            ans += min(leftHighest[i], rightHighest[i]) - height[i];
        }
        return ans;
    }
};

3. 二叉树中的最大路径和【困难】

题目链接：https://leetcode.cn/problems/binary-tree-maximum-path-sum/
参考题解：https://leetcode.cn/problems/binary-tree-maximum-path-sum/solution/er-cha-shu-zhong-de-zui-da-lu-jing-he-by-leetcode-/

3.1 题目描述

二叉树中的路径被定义为一条节点序列，序列中每对相邻节点之间都存在一条边。同一个节点在一条路径序列中 至多出现一次 。该路径 至少包含一个 节点，且不一定经过根节点。

路径和 是路径中各节点值的总和。

给你一个二叉树的根节点 root ，返回其 最大路径和 。

示例1：
在这里插入图片描述

输入：root = [1,2,3]
输出：6
解释：最优路径是 2 -> 1 -> 3 ，路径和为 2 + 1 + 3 = 6

示例2：
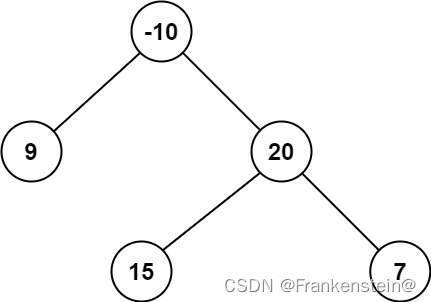
在这里插入图片描述

输入：root = [-10,9,20,null,null,15,7]
输出：42
解释：最优路径是 15 -> 20 -> 7 ，路径和为 15 + 20 + 7 = 42

提示：

树中节点数目范围是 [1, 3 * 10^4]
-1000 <= Node.val <= 1000

3.2 解题思路

每一条路径其实都可以看做是一个根节点加上左右两条子路径组成的。因此可以对每个节点求其左右最长的子路径，也可以理解成以该节点出发，往左边或者右边最长的路径。注意，由于节点存在负值，因此左右最长的子路径可能为0。要求的整个树的最长路径，就是在遍历各个节点过程中遇到的最大的节点值 + 左最长的子路径值 + 右最长的子路径值。而在求各个节点最长的子路径时，可以递归实现，分别递归求左子树和右子树里最长的子路径，然后取二者中的较大值。

3.3 代码实现

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int maxSubPathSum(TreeNode* root, int &ans) {
        if(!root)
            return 0;
        int leftMax = max(maxSubPathSum(root->left, ans), 0);
        int rightMax = max(maxSubPathSum(root->right, ans), 0);
        ans = max(ans, root->val + leftMax + rightMax);
        return max(leftMax, rightMax) + root->val;
    }
    int maxPathSum(TreeNode* root) {
        int ans = root->val;
        maxSubPathSum(root, ans);
        return ans;
    }
};

4. 二叉树的中序遍历【简单】

题目链接：https://leetcode.cn/problems/binary-tree-inorder-traversal/
参考题解：https://leetcode.cn/problems/binary-tree-inorder-traversal/solution/er-cha-shu-de-zhong-xu-bian-li-by-leetcode-solutio/

4.1 题目描述

给定一个二叉树的根节点 root ，返回 它的中序遍历 。

示例1：
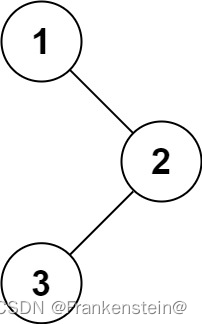
在这里插入图片描述

输入：root = [1,null,2,3]
输出：[1,3,2]

示例2：

输入：root = []
输出：[]

示例3：

输入：root = [1]
输出：[1]

提示：

树中节点数目在范围 [0, 100] 内
-100 <= Node.val <= 100

进阶： 递归算法很简单，你可以通过迭代算法完成吗？

4.2 解题思路

用“左根右”的顺序递归实现。

4.3 代码实现

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    void inorder(TreeNode* root, vector<int>& ans) {
        if(!root)
            return;
        inorder(root->left, ans);
        ans.push_back(root->val);
        inorder(root->right, ans);
    }
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> ans;
        inorder(root, ans);
        return ans;
    }
};

5. 删除链表的倒数第 N 个结点【中等】

题目链接：https://leetcode.cn/problems/remove-nth-node-from-end-of-list/
参考题解：https://leetcode.cn/problems/remove-nth-node-from-end-of-list/solution/shan-chu-lian-biao-de-dao-shu-di-nge-jie-dian-b-61/

5.1 题目描述

给你一个链表，删除链表的倒数第 n 个结点，并且返回链表的头结点。

示例1：
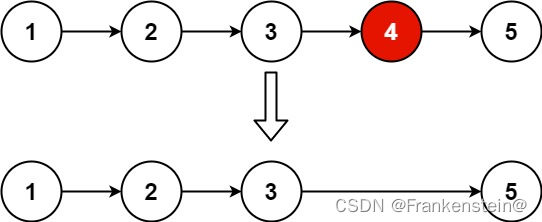
在这里插入图片描述

输入：head = [1,2,3,4,5], n = 2
输出：[1,2,3,5]

示例2：

输入：head = [1], n = 1
输出：[]

示例3：

输入：head = [1,2], n = 1
输出：[1]

提示：

链表中结点的数目为 sz
1 <= sz <= 30
0 <= Node.val <= 100
1 <= n <= sz

进阶： 你能尝试使用一趟扫描实现吗？

5.2 解题思路

用两个指针，一个先顺着链表往后移动 n 下，然后两个指针再同时往后移。如果两个指针开始时都指向头结点，那么后移动的指针最终指向的就是要删除的节点。实际上可以让后移动的节点先指向一个辅助头节点，这样一来该指针最终指向的就是要删除的节点的前一个节点，可以直接完成删除。

5.3 代码实现

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* removeNthFromEnd(ListNode* head, int n) {
        ListNode* right = head;
        ListNode* dummy = new ListNode(0, head);
        ListNode* left = dummy;
        for(int i = 0; i < n; ++i)
            right = right->next;
        while(right) {
            right = right->next;
            left = left->next;
        }
        left->next = left->next->next;
        return dummy->next;
    }
};