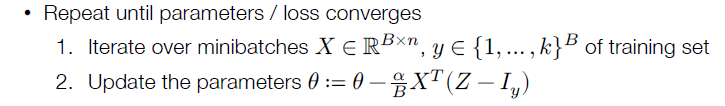文章目录
- 堆的介绍
- 堆的概念
- 堆的结构
- 堆的向下调整算法
- 建堆的时间复杂度
- 堆的向上调整算法
- 堆的基本功能实现
- 初始化堆
- 打印堆
- 堆的插入
- 堆的删除
- 获取堆顶的数据
- 获取堆的数据个数
- 堆的判空
- 销毁堆
堆的介绍
堆的概念
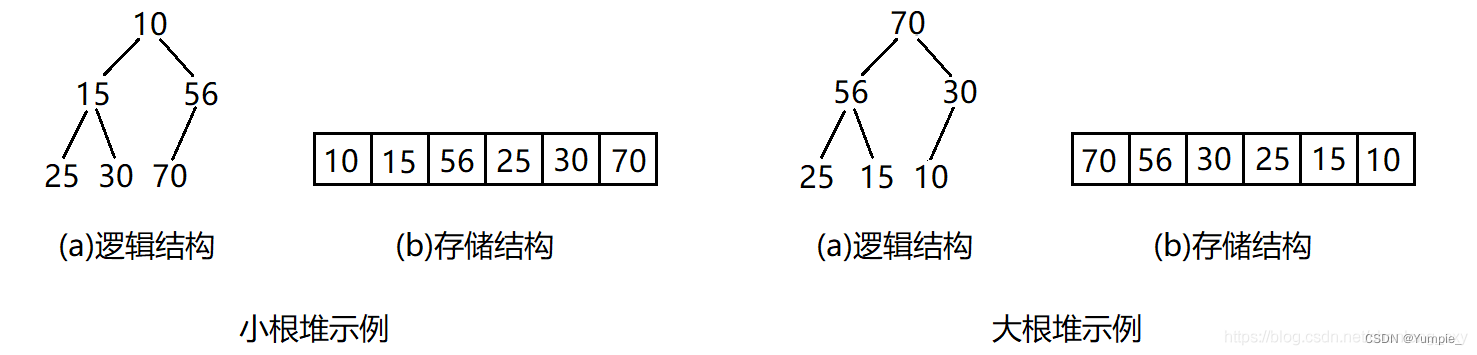
堆:如果有一个关键码的集合K={k0,k1,k2,…,kn-1},把它的所有元素按完全二叉树的顺序存储方式存储在一个一维数组中,并满足ki<=k2i+1且ki<=k2i+2(或满足ki>=k2i+1且ki>=k2i+2),其中i=0,1,2,…,则称该集合为堆。
小堆:将根结点最小的堆叫做小堆,也叫最小堆或小根堆。
大堆:将根结点最大的堆叫做大堆,也叫最大堆或大根堆。
堆的性质:
堆中某个结点的值总是不大于或不小于其父结点的值。
堆总是一棵完全二叉树。
堆的结构
堆的向下调整算法
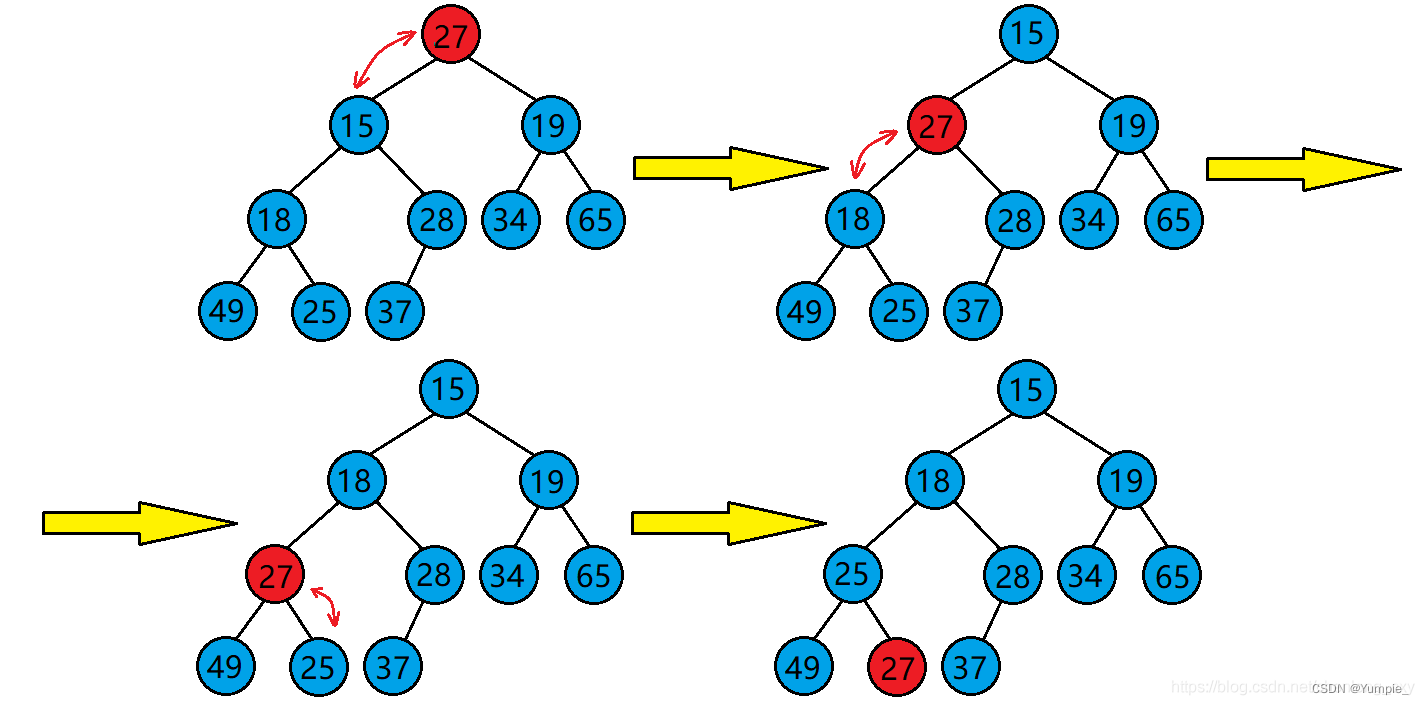
现在我们给出一个数组,逻辑上看作一棵完全二叉树。我们通过从根节点开始的向下调整算法可以把它调整成一个小堆。
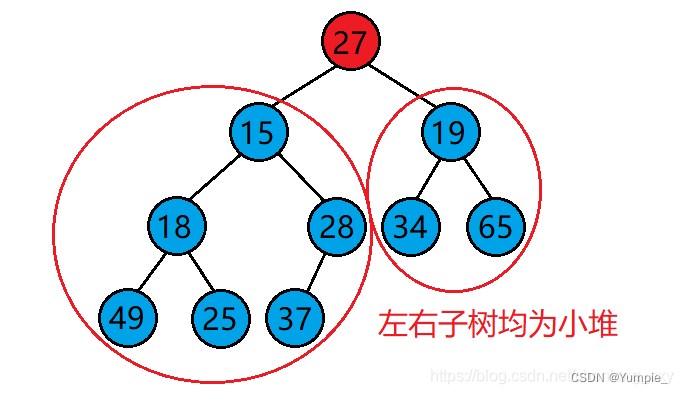
但是,使用向下调整算法需要满足一个前提:
若想将其调整为小堆,那么根结点的左右子树必须都为小堆。
若想将其调整为大堆,那么根结点的左右子树必须都为大堆。
向下调整算法的基本思想(以建小堆为例):
1.从根结点处开始,选出左右孩子中值较小的孩子。
2.让小的孩子与其父亲进行比较。
若小的孩子比父亲还小,则该孩子与其父亲的位置进行交换。并将原来小的孩子的位置当成父亲继续向下进行调整,直到调整到叶子结点为止。
若小的孩子比父亲大,则不需处理了,调整完成,整个树已经是小堆了。
代码实例:
//交换函数
void Swap(int* x, int* y)
{
int tmp = *x;
*x = *y;
*y = tmp;
}
//堆的向下调整(小堆)
void AdjustDown(int* a, int n, int parent)
{
//child记录左右孩子中值较小的孩子的下标
int child = 2 * parent + 1;//先默认其左孩子的值较小
while (child < n)
{
if (child + 1 < n&&a[child + 1] < a[child])//右孩子存在并且右孩子比左孩子还小
{
child++;//较小的孩子改为右孩子
}
if (a[child] < a[parent])//左右孩子中较小孩子的值比父结点还小
{
//将父结点与较小的子结点交换
Swap(&a[child], &a[parent]);
//继续向下进行调整
parent = child;
child = 2 * parent + 1;
}
else//已成堆
{
break;
}
}
}
使用堆的向下调整算法(调整一次),最坏的情况下(即一直需要交换结点),需要循环的次数为:h - 1 次(h为树的高度)。而h = log2(N+1)(N为树的总结点数)。所以堆的向下调整算法的时间复杂度为:O(logN) 。
上面说到,使用堆的向下调整算法需要满足其根结点的左右子树均为大堆或是小堆才行,那么如何才能将一个任意树调整为堆呢?
答案很简单,我们只需要从倒数第一个非叶子结点开始,从后往前,按下标,依次作为根去向下调整即可。
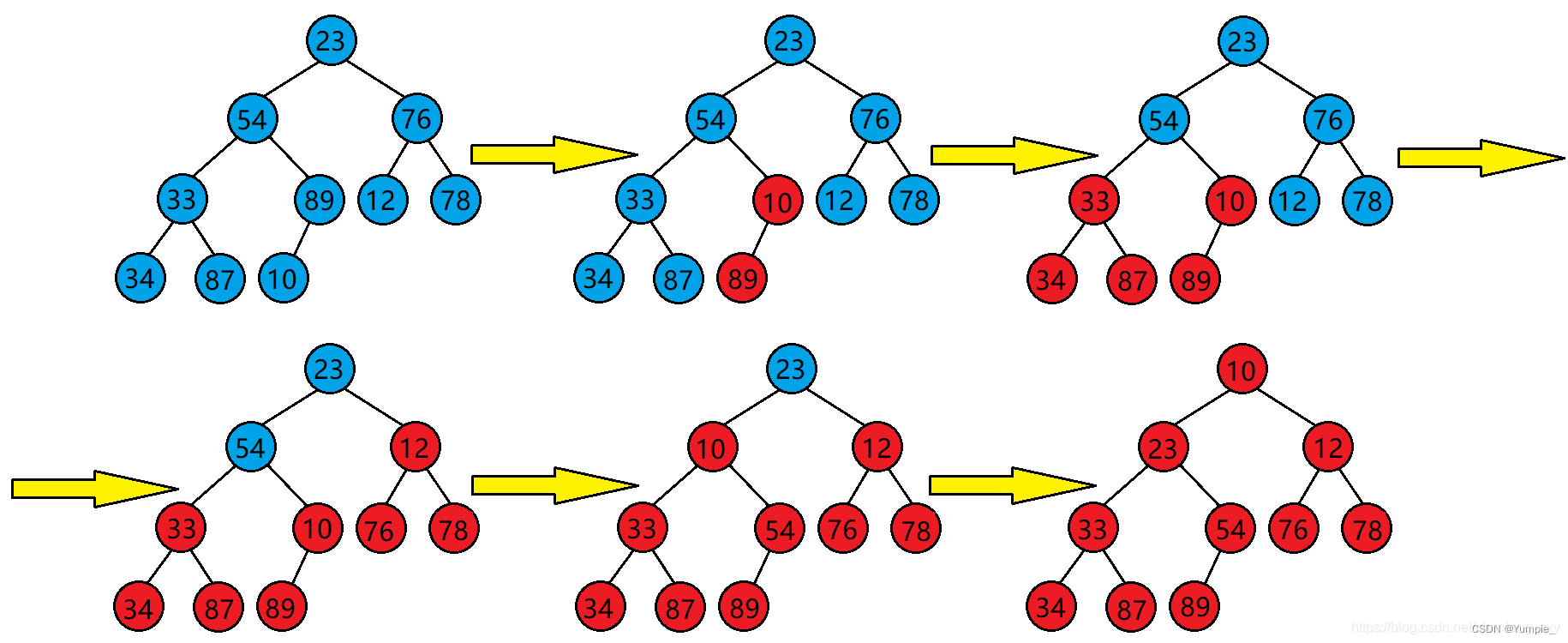
代码实例:
//建堆
for (int i = (n - 1 - 1) / 2; i >= 0; i--)
{
AdjustDown(php->a, php->size, i);
}
建堆的时间复杂度
那么建堆的时间复杂度又是多少呢?
当结点数无穷大时,完全二叉树与其层数相同的满二叉树相比较来说,它们相差的结点数可以忽略不计,所以计算时间复杂度的时候我们可以将完全二叉树看作与其层数相同的满二叉树来进行计算。
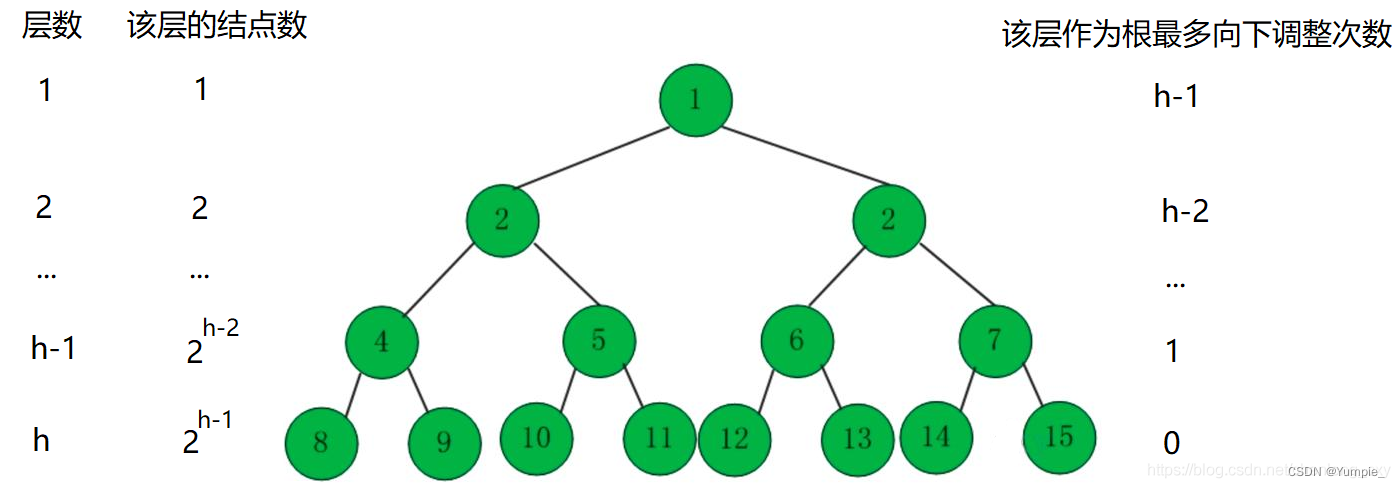

总结一下:
堆的向下调整算法的时间复杂度:T ( n ) = O ( log N ) T(n)=O(\log N)T(n)=O(logN)。
建堆的时间复杂度:T ( n ) = O ( N ) T(n)=O(N)T(n)=O(N)。
堆的向上调整算法
当我们在一个堆的末尾插入一个数据后,需要对堆进行调整,使其仍然是一个堆,这时需要用到堆的向上调整算法。
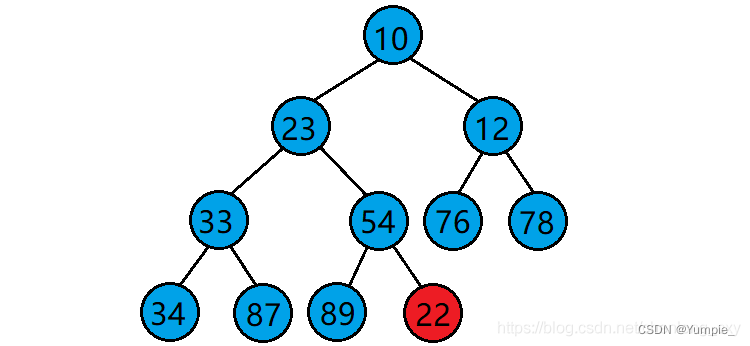
向上调整算法的基本思想(以建小堆为例):
1.将目标结点与其父结点比较。
2.若目标结点的值比其父结点的值小,则交换目标结点与其父结点的位置,并将原目标结点的父结点当作新的目标结点继续进行向上调整。若目标结点的值比其父结点的值大,则停止向上调整,此时该树已经是小堆了。
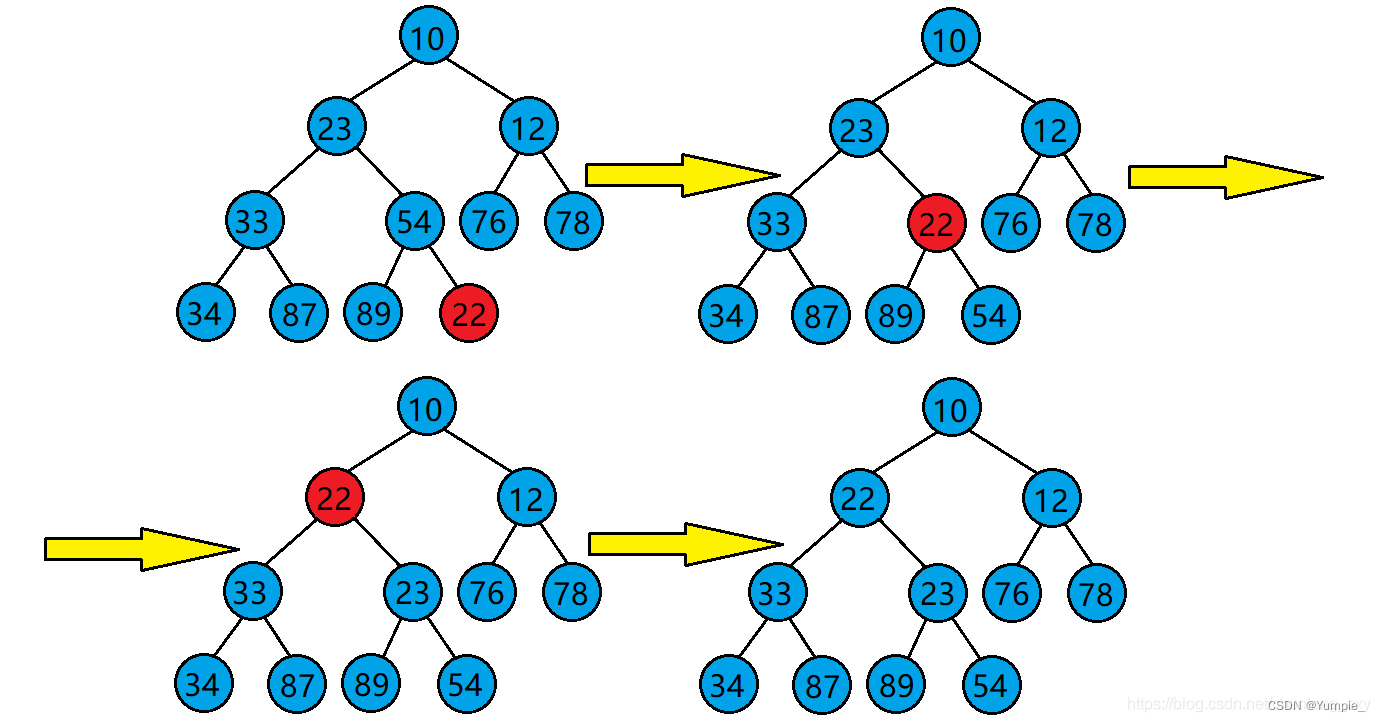
代码示例:
//交换函数
void Swap(HPDataType* x, HPDataType* y)
{
HPDataType tmp = *x;
*x = *y;
*y = tmp;
}
//堆的向上调整(小堆)
void AdjustUp(HPDataType* a, int child)
{
int parent = (child - 1) / 2;
while (child > 0)//调整到根结点的位置截止
{
if (a[child] < a[parent])//孩子结点的值小于父结点的值
{
//将父结点与孩子结点交换
Swap(&a[child], &a[parent]);
//继续向上进行调整
child = parent;
parent = (child - 1) / 2;
}
else//已成堆
{
break;
}
}
}
堆的基本功能实现
初始化堆
首先,必须创建一个堆类型,该类型中需包含堆的基本信息:存储数据的数组、堆中元素的个数以及当前堆的最大容量。
typedef int HPDataType;//堆中存储数据的类型
typedef struct Heap
{
HPDataType* a;//用于存储数据的数组
int size;//记录堆中已有元素个数
int capacity;//记录堆的容量
}HP;
然后我们需要一个初始化函数,对刚创建的堆进行初始化,注意在初始化期间要将传入数据建堆。
//初始化堆
void HeapInit(HP* php, HPDataType* a, int n)
{
assert(php);
HPDataType* tmp = (HPDataType*)malloc(sizeof(HPDataType)*n);//申请一个堆结构
if (tmp == NULL)
{
printf("malloc fail\n");
exit(-1);
}
php->a = tmp;
memcpy(php->a, a, sizeof(HPDataType)*n);//拷贝数据到堆中
php->size = n;
php->capacity = n;
int i = 0;
//建堆
for (i = (php->size - 1 - 1) / 2; i >= 0; i--)
{
AdjustDown(php->a, php->size, i);
}
}
打印堆
打印堆中的数据,这里用了两种打印格式。
第一种打印格式是按照堆的物理结构进行打印,即打印为一排连续的数字。
第二种打印格式是按照堆的逻辑结构进行打印,即打印成树形结构。
//求结点数为n的二叉树的深度
int depth(int n)
{
assert(n >= 0);
if (n>0)
{
int m = 2;
int hight = 1;
while (m < n + 1)
{
m *= 2;
hight++;
}
return hight;
}
else
{
return 0;
}
}
//打印堆
void HeapPrint(HP* php)
{
assert(php);
//按照物理结构进行打印
int i = 0;
for (i = 0; i < php->size; i++)
{
printf("%d ", php->a[i]);
}
printf("\n");
//按照树形结构进行打印
int h = depth(php->size);
int N = (int)pow(2, h) - 1;//与该二叉树深度相同的满二叉树的结点总数
int space = N - 1;//记录每一行前面的空格数
int row = 1;//当前打印的行数
int pos = 0;//待打印数据的下标
while (1)
{
//打印前面的空格
int i = 0;
for (i = 0; i < space; i++)
{
printf(" ");
}
//打印数据和间距
int count = (int)pow(2, row - 1);//每一行的数字个数
while (count--)//打印一行
{
printf("%02d", php->a[pos++]);//打印数据
if (pos >= php->size)//数据打印完毕
{
printf("\n");
return;
}
int distance = (space + 1) * 2;//两个数之间的空格数
while (distance--)//打印两个数之间的空格
{
printf(" ");
}
}
printf("\n");
row++;
space = space / 2 - 1;
}
}
堆的插入
数据插入时是插入到数组的末尾,即树形结构的最后一层的最后一个结点,所以插入数据后我们需要运用堆的向上调整算法对堆进行调整,使其在插入数据后仍然保持堆的结构。
//堆的插入
void HeapPush(HP* php, HPDataType x)
{
assert(php);
if (php->size == php->capacity)
{
HPDataType* tmp = (HPDataType*)realloc(php->a, 2 * php->capacity*sizeof(HPDataType));
if (tmp == NULL)
{
printf("realloc fail\n");
exit(-1);
}
php->a = tmp;
php->capacity *= 2;
}
php->a[php->size] = x;
php->size++;
//向上调整
AdjustUp(php->a, php->size - 1);
}
堆的删除
堆的删除,删除的是堆顶的元素,但是这个删除过程可并不是直接删除堆顶的数据,而是先将堆顶的数据与最后一个结点的位置交换,然后再删除最后一个结点,再对堆进行一次向下调整。
原因:我们若是直接删除堆顶的数据,那么原堆后面数据的父子关系就全部打乱了,需要全体重新建堆,时间复杂度为O ( N ) O(N)O(N)。若是用上述方法,那么只需要对堆进行一次向下调整即可,因为此时根结点的左右子树都是小堆,我们只需要在根结点处进行一次向下调整即可,时间复杂度是:O(log(N))。
//堆的删除
void HeapPop(HP* php)
{
assert(php);
assert(!HeapEmpty(php));
Swap(&php->a[0], &php->a[php->size - 1]);//交换堆顶和最后一个结点的位置
php->size--;//删除最后一个结点(也就是删除原来堆顶的元素)
AdjustDown(php->a, php->size, 0);//向下调整
}
获取堆顶的数据
获取堆顶的数据,即返回数组下标为0的数据。
//获取堆顶的数据
HPDataType HeapTop(HP* php)
{
assert(php);
assert(!HeapEmpty(php));
return php->a[0];//返回堆顶数据
}
获取堆的数据个数
获取堆的数据个数,即返回堆结构体中的size变量。
//获取堆中数据个数
int HeapSize(HP* php)
{
assert(php);
return php->size;//返回堆中数据个数
}
堆的判空
堆的判空,即判断堆结构体中的size变量是否为0。
//堆的判空
bool HeapEmpty(HP* php)
{
assert(php);
return php->size == 0;//判断堆中数据是否为0
}
销毁堆
为了避免内存泄漏,使用完动态开辟的内存空间后都要及时释放该空间,所以,一个用于释放内存空间的函数是必不可少的。
//销毁堆
void HeapDestroy(HP* php)
{
assert(php);
free(php->a);//释放动态开辟的数组
php->a = NULL;//及时置空
php->size = 0;//元素个数置0
php->capacity = 0;//容量置0
}