GNN

参考资料：https://www.bilibili.com/video/BV16v4y1b7x7

图网络为什么复杂

• 需要接受任意尺寸的输入
• 没有固定的节点顺序和参考锚点（比如文本是从前往后处理，图像是有像素点的，图没有起始点）
• 动态变化和多种模态的特征（比如音乐推荐）

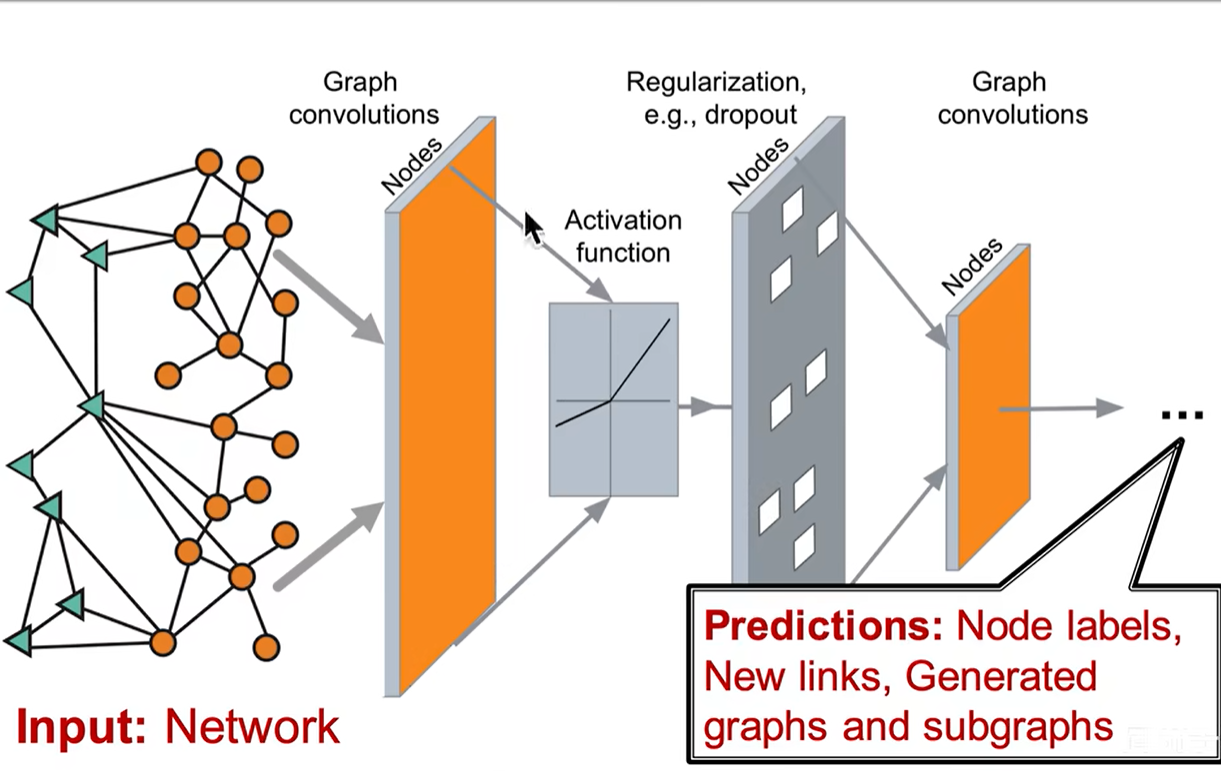
端到端

GNN 工具

PyG

GNN 库

NetworkX

构建图的库

DGL

李沐老师推荐，复现了很多顶会论文，适合做学术研究

图数据可视化工具

• AntV 可视化
• Echarts 可视化
• GraphGL

图数据库

Neo4j

图机器学习应用

• 最短路径搜索和查找
• 分析节点的重要性 PageRank
• 社交群体检测
• 社交网络，可能认识的人
• 相似度分析
• Embeddings 节点映射为一个向量，作为后续的机器学习

不同的任务

• 图层面：分子是否有毒，生成新的分子结构
• 节点层面：信用卡欺诈
• 子图层面：用户聚类
• 边层面：推荐可能认识的人

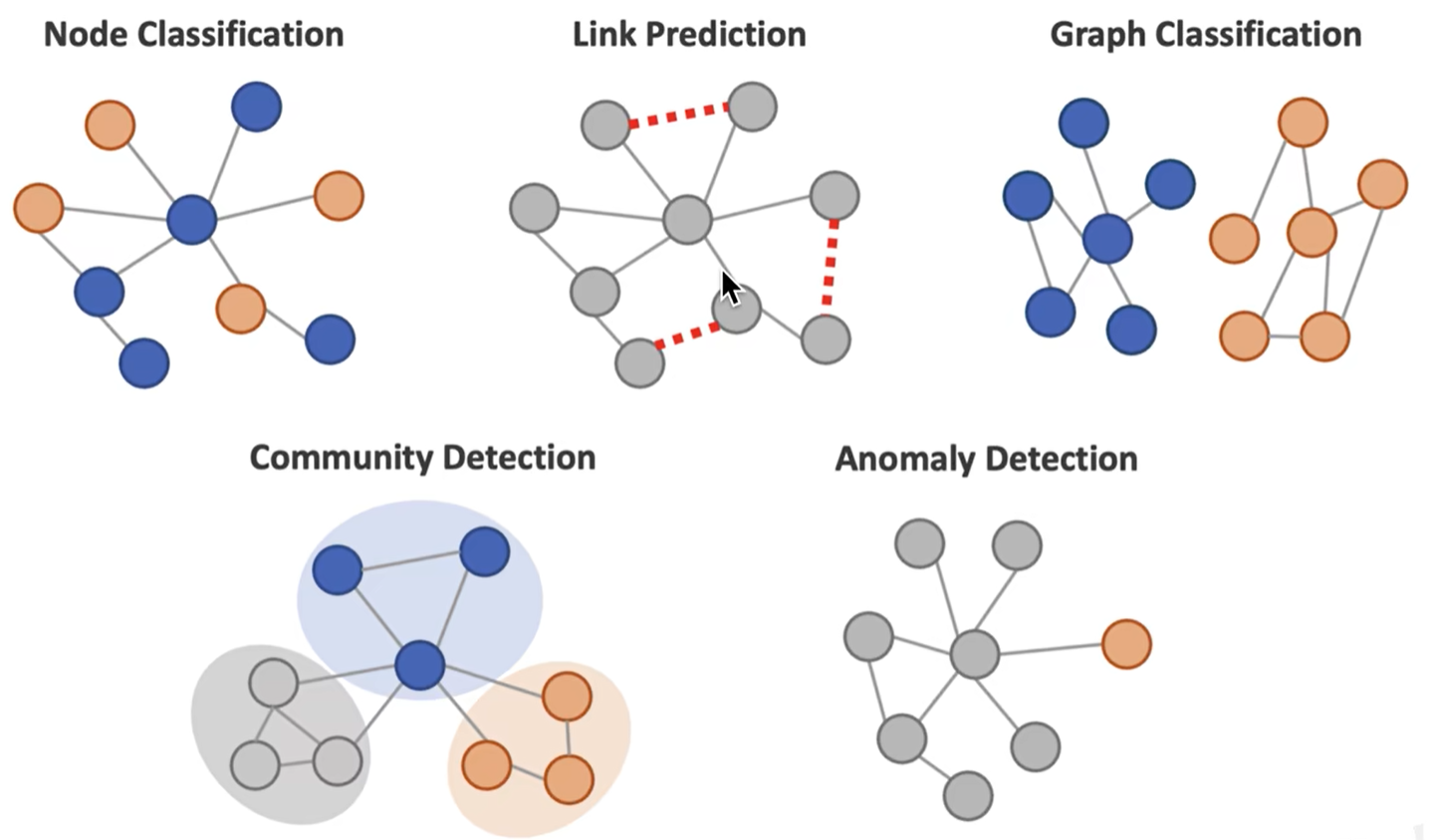
图数据挖掘应用

• ReadPaper
• Connected paper
• Bios
• 刘焕勇

Google 插件

Hypercrx

OpenRank

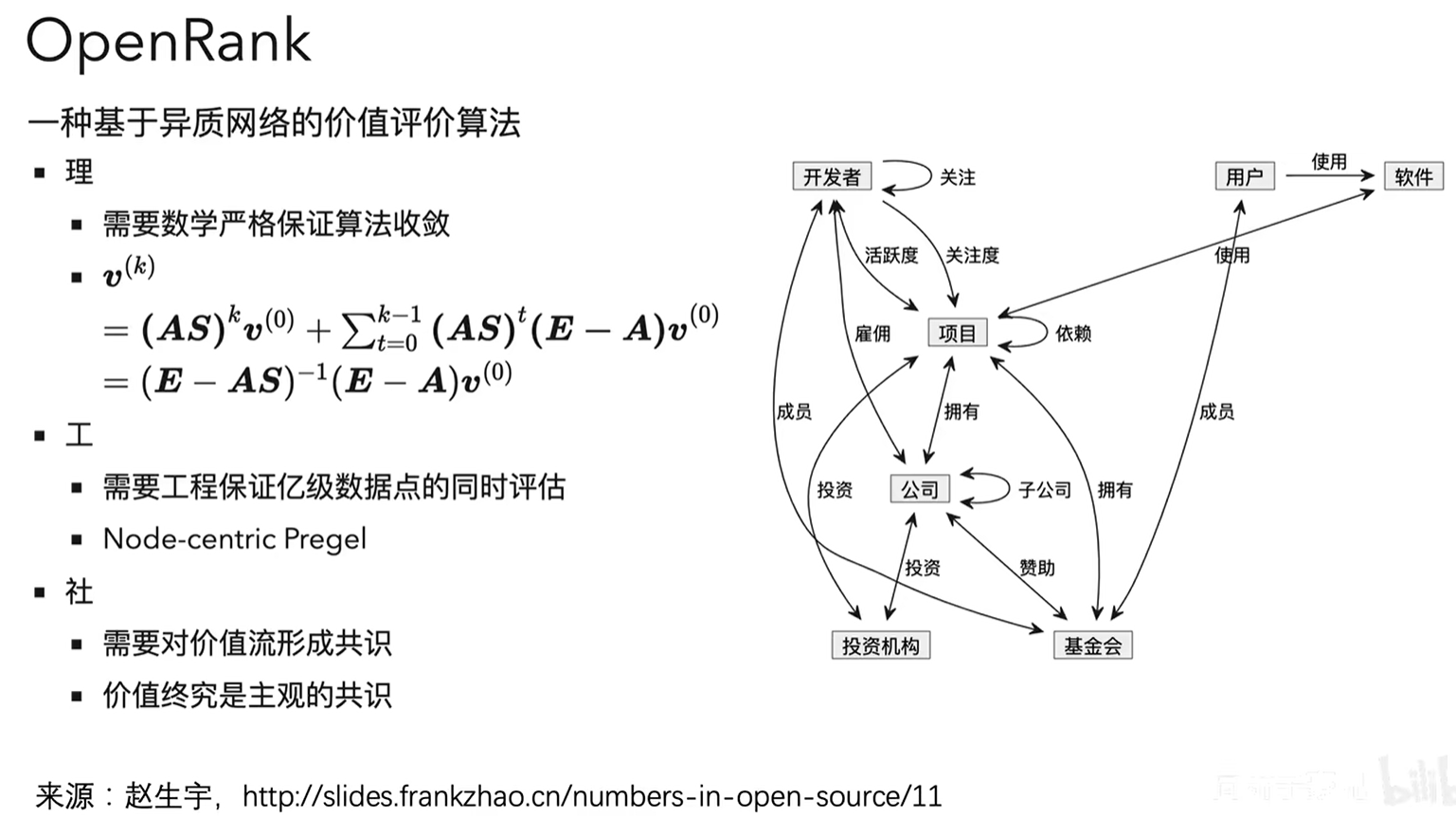
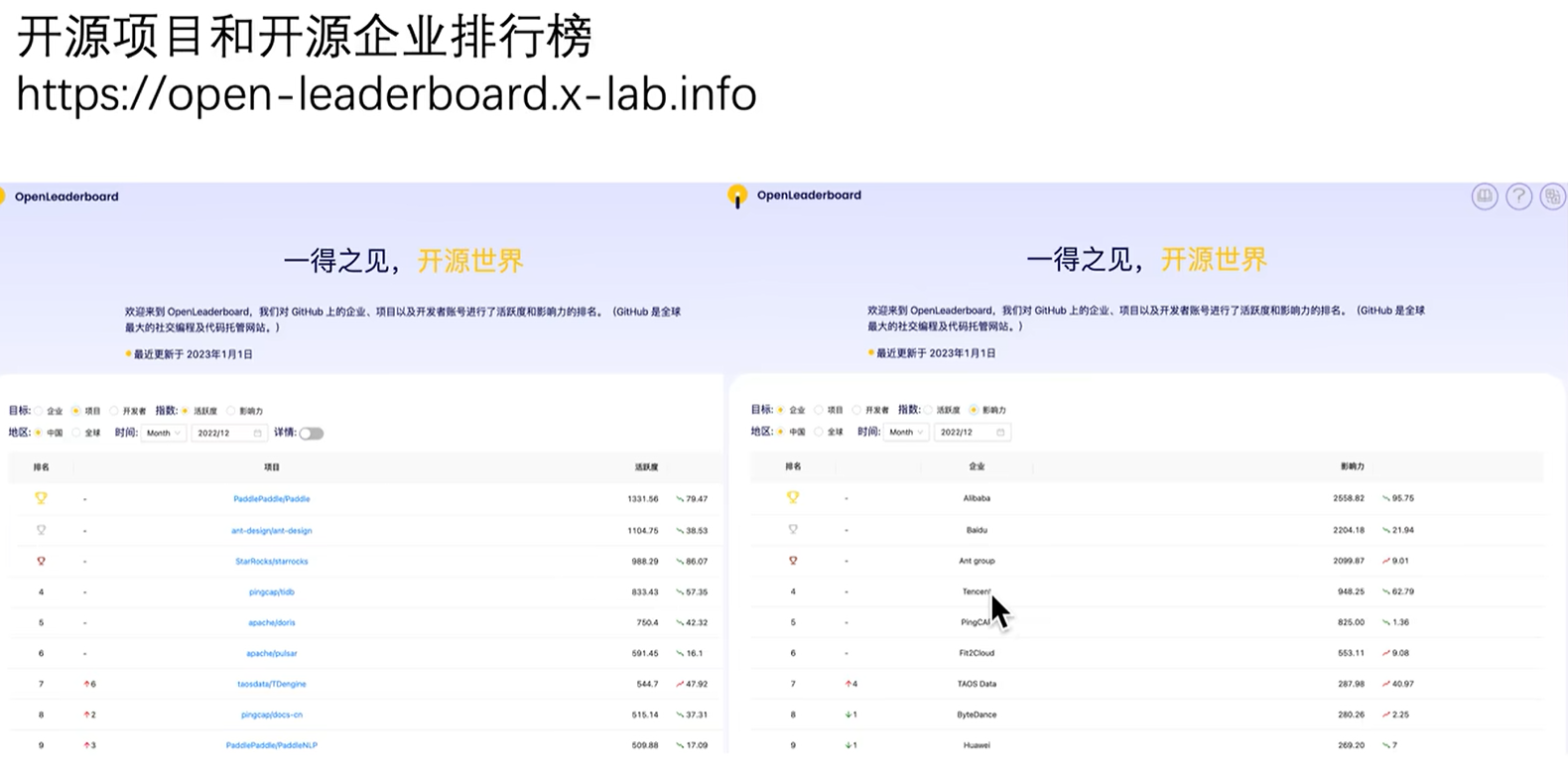
1. 图的基本表示

• 图的本体设计
• 图的种类（有向，无向，异质，二分，连接带权重）
• 节点连接数
• 图的基本表示-邻接矩阵
• 图的基本表示-连接列表和邻接列表
• 图的连通性

1.1 本体图 Ontology

如何设计图的本体，取决于将来想解决什么问题。

抽象图叫做本体图

1.2 无向图

对称的，互相的，双向的

比如：

• 合作关系
• Facebook 的好友关系

1.3 有向图

比如：

• 打电话
• Facebook 的关注

1.4 异质图

节点有不同的类型，连接也有不同的类型

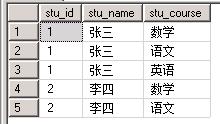
1.5 二分图，比较特殊的异质图

只有两种类型的节点

比如：

• 论文和作者
• 演员和电影
• 用户和电影（评分）
• 菜谱和食材

展开二分图

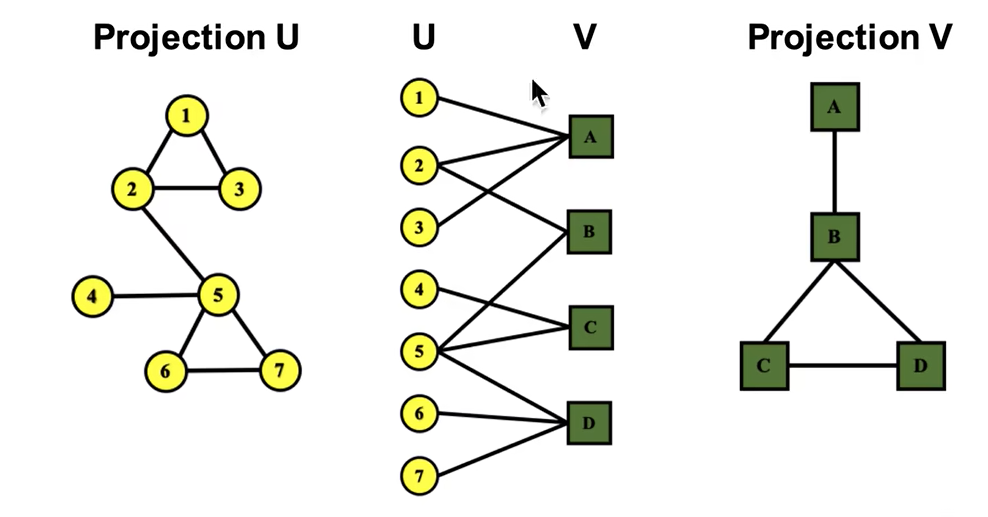
将 U 和 V 各自的连通关系分别进行分析挖掘。

1.6 Node Degree

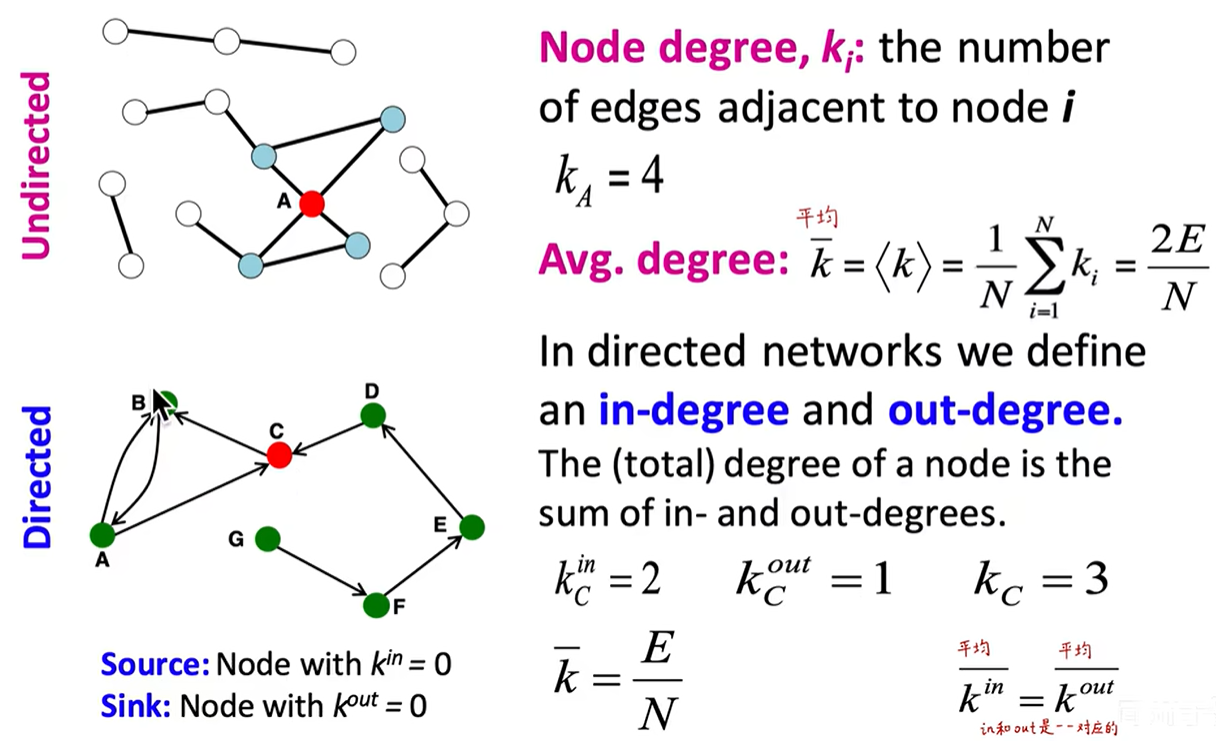
使用 Node Degree 可以展示一个节点的重要性

Note：
为什么要把图表示成矩阵的形式？

• 保留了图全部的信息
• 适合矩阵加速运算

稀疏矩阵适合连接列表和邻接列表的表示。

1.7 其他图

• 带权边图
• Self-edges
• Multigragh，两个节点有多条道路

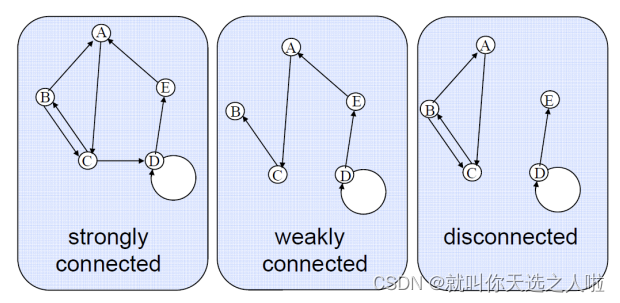
1.8 图的术语

强连通：有向图任意两个节点可以相互触达

弱联通：忽略方向是联通的

强连通域：

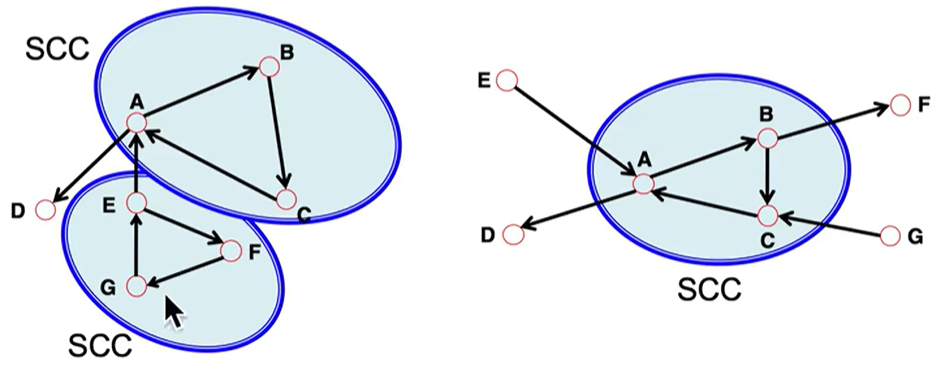
2. 传统图机器学习和特征工程

2.0 图机器学习基本任务

• 节点层面
• 连接层面
• 图层面

2.1 图机器学习

目标：对一系列目标进行预测

可选设计：

• 将节点变为 d 维向量
• 全图变成 d 维向量

让算法去拟合一个边界

2.2 节点层面的特征工程

给定一个图 $G=(V,E)$

学习一个函数 $f:v\to R$

• 输入某个节点的 d 维向量，输出该节点是某类的概率

由已知的节点去预测未知节点，称作半监督节点分类问题（训练时用到了未标记节点的特征）

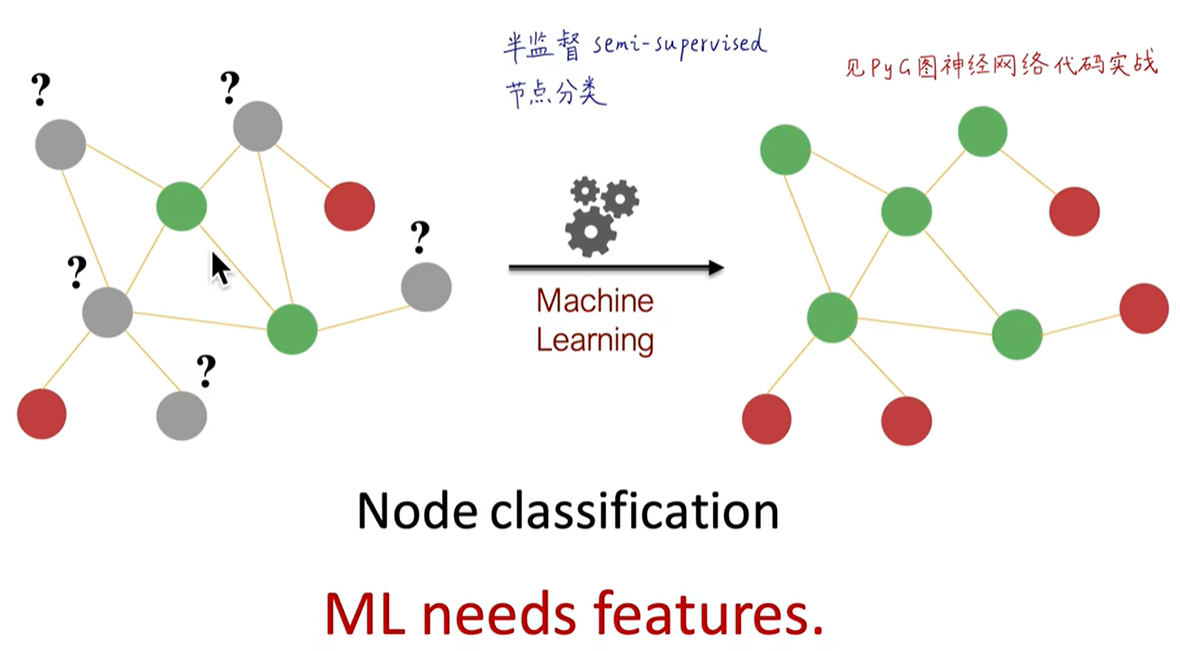
2.2.1 特征向量中心性

https://blog.csdn.net/myy3075/article/details/87948777

2.3 连接层面的特征工程

通过已知连接补全未知连接

• 直接提取 link 的特征，把 link 变成 d 维向量（√）
• 把 link 的两端的节点的 d 维向量拼起来（×）丢失了 link 本身的连接结构信息

a.基于两节点距离：

两点间最短路径的长度 distance-based feature

缺点：这种方式的问题在于没有考虑两个点邻居的重合度（the degree of neighborhood overlap），如B-H有2个共同邻居，B-E和A-B都只有1个共同邻居。

b.基于两节点局部连接信息

共同的邻居的问题在于度数高的点对就会有更高的结果，Jaccard的系数是其归一化后的结果。Adamic-Adar指数在实践中表现得好。在社交网络上表现好的原因：有一堆度数低的共同好友比有一堆名人共同好友的得分更高。

c.基于两节点在全图的连接信息

local neighborhood overlap的限制在于，如果两个点没有共同邻居，值就为0。

但是这两个点未来仍有可能被连接起来。所以我们使用考虑全图的global neighborhood overlap来解决这一问题，主要计算Katz index。
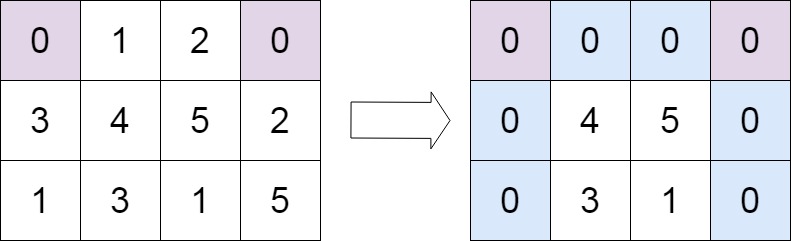
Katz index：计算点对之间所有长度路径的条数
计算方式：邻接矩阵求幂
邻接矩阵的k次幂结果，每个元素就是对应点对之间长度为k的路径的条数

2.4 全图层面的特征工程

图级别特征构建目标：找到能够描述全图结构的特征。

2.4.1 Kernel Methods

类似于SVM的核函数，定义好以后，通过核函数矩阵的映射，就可以按照之前的方式来处理了。

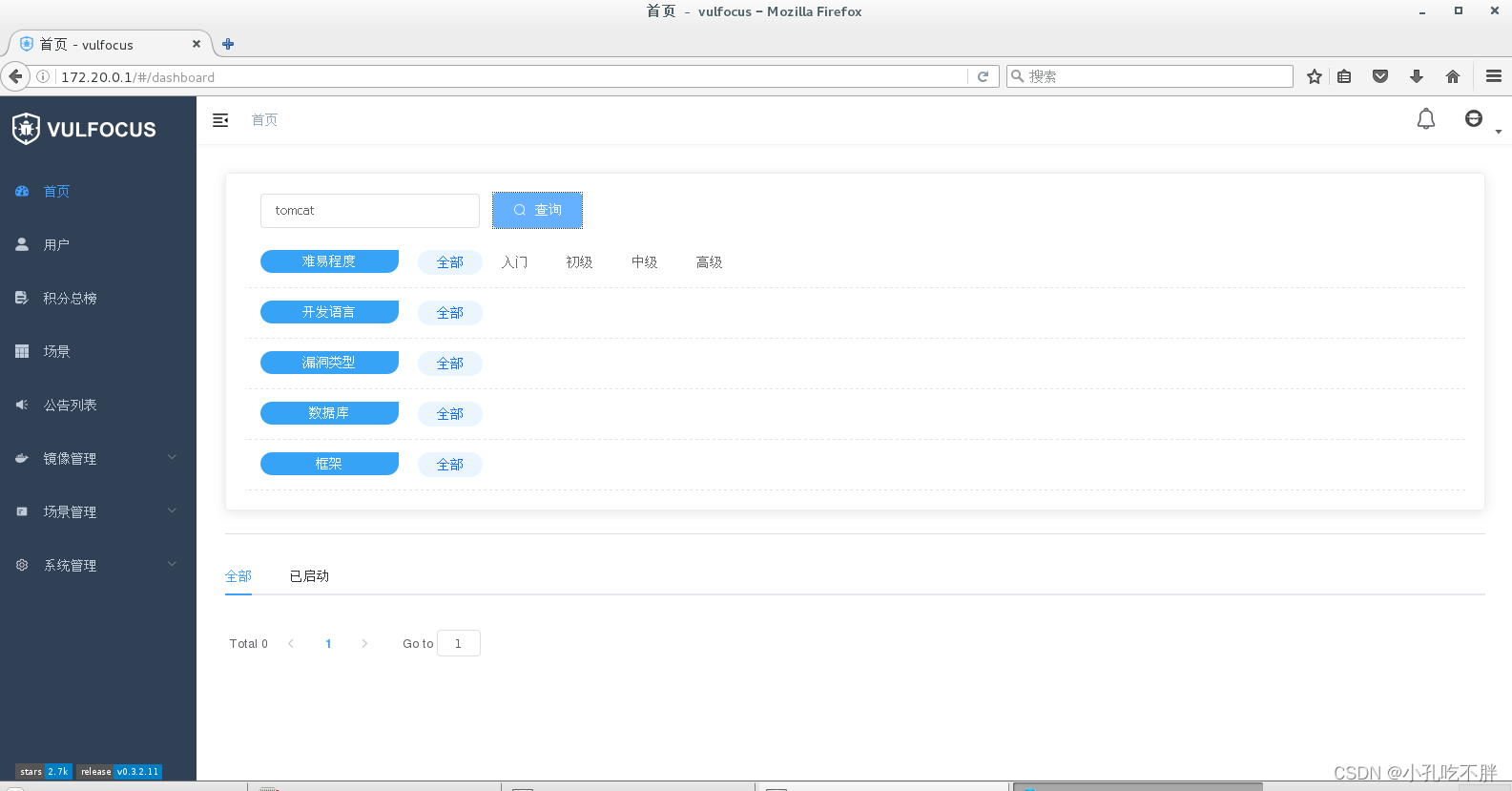
2.5 NetworkX 实战

3. 图嵌入表示学习

将节点变成一个低维向量用于机器学习算法

3.1 DeepWalk

类似 Word2Vec，在图上随机游走，游走序列可以看成一个句子，一个节点可以看成一个单词。

采用类似 skip-gram 的算法，输入中心节点，预测周围临近节点

算法步骤：

1. 输入图
2. 随机游走
3. 训练嵌入向量
4. 为了解决分类个数过多的问题，加一个分层 Softmax（霍夫曼编码数），每次分类可以排除一半的类别数
5. 得到每个节点的嵌入向量

Note：
贡献：

• 首个将深度学习和 NLP 领域的知识用于图机器学习
• 在稀疏标注节点分类场景下，嵌入性能卓越
  缺陷：
• 均匀随机游走，没有偏向的游走方向（Node2Vec 改进）
• 需要大量随机游走序列训练
• 基于随机游走，管中窥豹。距离较远的两个节点无法相互影响。看不到全图信息（GNN 改进）
• 无监督，仅编码图的连接信息，没有利用节点的属性特征
• 没有真正用到神经网络和深度学习

3.2 Node2Vec

Node2Vec 采用两种游走策略：

• DFS：同质社群（社交网络）
• BFS：节点功能角色（中枢，桥接，边缘）

抽样算法：https://www.keithschwarz.com/darts-dice-coins/

alibaba 商品推荐：

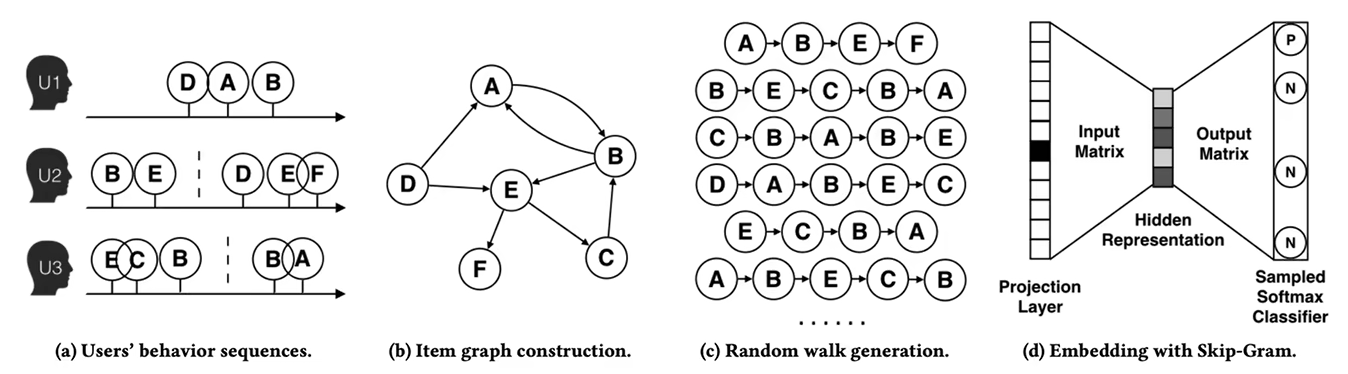
Note：

4. PageRank

TOFIX

转移矩阵每一列非零位置的概率相等，且和为 1。

PageRank 收敛性分析：

Ergodic theory

5. 半监督节点分类：标签传播和消息传递

TOFIX

6. GNN

将节点映射为 d 维向量，向量具有三个特征：

• 低维：向量维度远小于节点数
• 连续：每个元素都是实数（有正有负）
• 稠密：每个元素都不为 0

表示学习：从数据中提取最少必要信息

图嵌入、节点表示学习：把节点映射为低维连续稠密向量

向量点乘数值（余弦相似度）反映节点的相似度

邻接矩阵包含了所有的节点信息和连接信息。

Naive Approach

Note：
邻接矩阵既然包含了节点和相互连接的所有信息,那么能否直接将邻接矩阵输入神经网络呢?

把每一行对应的特征输入到神经网络中去。

这样会出现几个缺点：

• 节点过多内存会炸
• 参数量太大，容易过拟合
• 新节点加入，需要重新训练，无法进行泛化
• 不具备 “变换不变性”