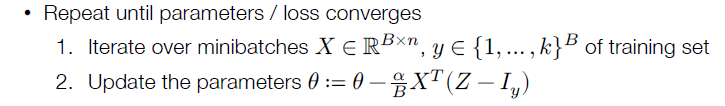机器学习算法的三个主要部分
- The hypothesis class: 模型结构
- loss fuction 损失函数
- An optimization method:在训练集上减小loss的方法
多分类问题
- 训练数据: x ( i ) ∈ R n , y ( i ) ∈ 1 , . . . , k f o r i = 1 , . . . m x^{(i)}\in \mathbb{R}^n ,y^{(i)}\in {1,...,k} for i=1,...m x(i)∈Rn,y(i)∈1,...,kfori=1,...m
- n 是输入数据的维度,输入的每一例数据是一个n维向量
- k 是要分成的类的数量
- m 是训练集的大小,总共有m例数据
线性假设函数
假设函数
h
:
R
n
→
R
k
h:\mathbb{R}^n \rightarrow\mathbb{R}^k
h:Rn→Rk
其中
h
i
(
x
)
h_i(x)
hi(x) 用来衡量划分到类 i 的可能性
一个线性的假设函数
h
θ
(
x
)
=
θ
T
x
h_{\theta}(x)=\theta^Tx
hθ(x)=θTx
参数
θ
∈
R
n
×
k
\theta\in\mathbb{R}^{n\times k}
θ∈Rn×k
矩阵形式
X
∈
R
m
×
n
=
[
x
(
1
)
T
.
.
.
x
(
m
)
T
]
,
y
∈
1
,
.
.
.
,
k
m
=
[
y
(
1
)
.
.
.
y
(
m
)
]
X\in \mathbb{R}^{m\times n} = \begin{bmatrix} x^{(1)T} \\ ... \\ x^{(m)T} \end{bmatrix}, y\in{1,...,k}^m=\begin{bmatrix}y^{(1)} \\ ... \\ y^{(m)}\end{bmatrix}
X∈Rm×n=
x(1)T...x(m)T
,y∈1,...,km=
y(1)...y(m)
线性假设函数可以写成下面的形式
h θ ( X ) = [ h θ ( x ( 1 ) ) T . . . h θ ( x ( m ) ) T ] = [ x ( 1 ) T θ . . . x ( 1 ) T θ ] = X θ h_\theta(X) = \begin{bmatrix}h_{\theta}(x^{(1)})^T \\... \\h_{\theta}(x^{(m)})^T \end{bmatrix}= \begin{bmatrix}x^{(1)T}\theta \\...\\x^{(1)T} \theta\end{bmatrix} = X\theta hθ(X)= hθ(x(1))T...hθ(x(m))T = x(1)Tθ...x(1)Tθ =Xθ
损失函数1 classification error
这个损失函数,不可微,对于optimization是非常不好用的
ℓ e r r ( h ( x ) , y ) = { 0 , i f a r g m a x i h i ( x ) = y 1 , o t h e r w i s \ell_{err}(h(x),y) = \left\{\begin{matrix} 0\quad ,if\quad argmax_i\quad h_i(x)=y \\ 1\quad ,otherwis \end{matrix}\right. ℓerr(h(x),y)={0,ifargmaxihi(x)=y1,otherwis
损失函数2 softmax / cross-entropy loss
z i = p ( l a b e l = i ) = e x p ( h i ( x ) ) ∑ j = 1 k e x p ( h j ( x ) ) ⟺ z = n o r m a l s i z e ( e x p ( h ( x ) ) ) z_i = p(label=i)=\frac{exp(h_i(x))}{\sum_{j=1}^kexp(h_j(x))} \Longleftrightarrow z = normalsize(exp(h(x))) zi=p(label=i)=∑j=1kexp(hj(x))exp(hi(x))⟺z=normalsize(exp(h(x)))
zi 表示分类为i的概率,将假设函数的输出转为概率。
softmax 或者交叉熵损失
ℓ e r r ( h ( x ) , y ) = − log p ( l a b e l = y ) = − h y ( x ) + log ∑ j = 1 k e x p ( h j ( x ) ) \ell_{err}(h(x),y) =- \log p(label=y)= -h_y(x)+\log \sum_{j=1}^kexp(h_j(x)) ℓerr(h(x),y)=−logp(label=y)=−hy(x)+logj=1∑kexp(hj(x))
softmax 回归优化问题
接下来的任务就是想办法减小损失函数
min θ 1 m ∑ i = 1 m ℓ ( h θ ( x ( i ) ) , y ( i ) ) \min_{\theta} \frac{1}{m}\sum_{i=1}^m\ell(h_\theta(x^{(i)}),y^{(i)}) θminm1i=1∑mℓ(hθ(x(i)),y(i))
如何找到 θ \theta θ来减少损失函数呢?
优化:梯度下降法
对一个输入为矩阵,输出为标量的函数 f : R n × k → R f:\mathbb{R}^{n\times k} \rightarrow \mathbb{R} f:Rn×k→R ,以下为梯度的定义,针对 θ \theta θ的每一个元素求偏导。
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-hcojNuCy-1684499011760)(null)]
梯度指示了增长最快的方向。
更新 θ \theta θ
θ : = θ − α ▽ θ f ( θ ) \theta:=\theta - \alpha \triangledown_\theta f(\theta) θ:=θ−α▽θf(θ)
α \alpha α 是学习率,用来控制更新的步长
随机梯度下降
不使用所有的数据来更新参数,每次选择一个 minibatch ,针对minibatch求loss和梯度及进行更新
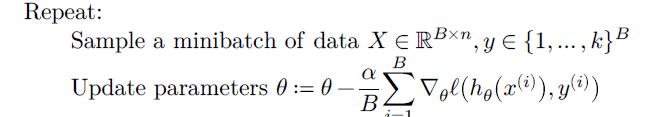
回到我们的问题,如何计算softmax损失函数的梯度?
h = θ T x , h ∈ R k h = \theta^Tx,h\in \mathbb{R}^k h=θTx,h∈Rk
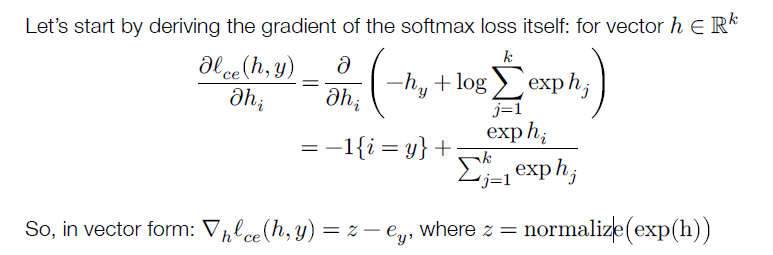
e
y
e_y
ey 是一个向量,只有y位置为1,其余位置为0
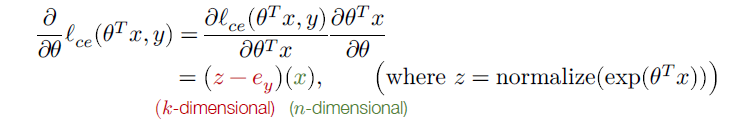
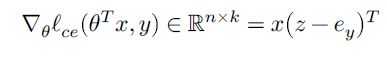
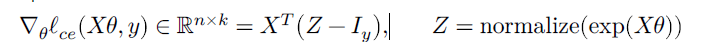
X T ∈ R n × m X^T \in \mathbb{R}^{n\times m} XT∈Rn×m Z − I y ∈ R m × k Z -I_y \in \mathbb{R}^{m\times k} Z−Iy∈Rm×k
总的过程为
先选择一个minibatch,再更新
θ
\theta
θ