01 常规的相关系数简单说明

在研究滑动窗口前，我们先来研究一下常规的相关系数分析，为了简化问题，假定我们现在有四川省范围内2019年每月的降水量数据和NDVI影像，我们想研究不同区域降水量和NDVI的相关性，即研究降水量和NDVI的空间关联性。

基本思路就是：对于每一个像元，都有1~12月共计12个值的降水量和NDVI指数，那么基于这两列数据我们可以计算出该像元位置降水量和NDVI的相关系数（这里我比较推荐使用斯皮尔曼系数，因为皮尔逊系数要求我们的这两列数据满足正态分布，但实际上我们往往都是假定我们的数据满足正态分布，这样计算的相关系数其实是有偏差的），对于每一个像元我们都可以计算出一个相关系数，如此便可以得到四川省范围内的相关系数的空间分布图。

思路讲完了，我们就可以得到如下的影像。

02 滑动窗口下的相关系数分析

重点来了，我们想看看在一定范围内的相关系数，怎么办？

说明：我当前有4个excel文件，分别为降水量数据，NDVI数据，地表温度数据，土壤水分数据。对于每一个excel文件，前5列表示地形因子数据，往后13列为2003年~2015年的降水量/NDVI/地表温度/土壤水分数据，每一行表示一个像元的地形因子值、气候因子值。

大致如下：

思路：假定滑动窗口为3*3（想想ArcGIS中空间分析工具-区域统计-焦点统计，有一点点类似），从第一个像元位置开始，对于该像元的移动窗口（包括其本身和周围8个像元），我们对于窗口内的每一个像元，都进行如下处理：获取窗口像元的降水量值(2003年~2015年共计13个值)和NDVI值，计算该像元位置的相关系数。那么对于该窗口我们一共计算了9个相关系数，然后我们计算这9个相关系数的平均值作为中心像元的相关系数值。类似的，对于降水量和地表温度、降水量和土壤水分均是如此操作。

以下是使用python实现的代码：

# @炒茄子  2023-05-18

import numpy as np
import pandas as pd
from scipy.stats import spearmanr
# 注意: 此处使用皮尔逊系数进行相关系数的计算, 但是皮尔逊系数要求数据满足正态分布, 但是实际上很多数据并不满足正态分布, 因此在此处尝试使用斯皮尔曼系数进行相关系数的计算
# 注意: 斯皮尔曼系数要求数据必须是有序的, 即数据具有可比较的大小关系
"""
当前程序用计算不同空间窗口下两两变量之间的相关系数，探索二者之间在空间上是否存在一定的关联。
"""
# 读取年平均降水量和 NDVI 数据、地表温度数据、土壤水分数据
precip_data_year = pd.read_excel(r'E:\PRCP\table\kinds_aver\precipitation_sc_year.xlsx', sheet_name='降水年平均值数据')
ndvi_data_year = pd.read_excel(r'E:\PRCP\table\kinds_aver\ndvi_sc_year.xlsx', sheet_name='NDVI年平均值数据')
temperature_data_year = pd.read_excel(r'E:\PRCP\table\kinds_aver\temperature_sc_year.xlsx', sheet_name='地表温度年平均值数据')
soil_moisture_data_year = pd.read_excel(r'E:\PRCP\table\kinds_aver\soil_moisture_sc_year.xlsx', sheet_name='土壤水分年平均值数据')
# 读取降水量数据和NDVI等数据(不读取地形因子和经纬度列)
_precip_data_year = precip_data_year.iloc[:, 5:]
_ndvi_data_year = ndvi_data_year.iloc[:, 5:]
_temperature_data_year = temperature_data_year.iloc[:, 5:]
_soil_moisture_data_year = soil_moisture_data_year.iloc[:, 5:]
# 创建空的三维数组，用于维度转换后的结果(83, 113, number_of_years)
precip_data_year = np.zeros((83, 113, len(_precip_data_year.columns)), dtype=np.float32)
ndvi_data_year = np.zeros((83, 113, len(_ndvi_data_year.columns)), dtype=np.float32)
temperature_data_year = np.zeros((83, 113, len(_temperature_data_year.columns)), dtype=np.float32)
soil_moisture_data_year = np.zeros((83, 113, len(_soil_moisture_data_year.columns)), dtype=np.float32)
# 将二维数组转换为三维数组
for i in range(len(_precip_data_year.columns)):
    precip_data_year[:, :, i] = _precip_data_year.iloc[:, i].values.reshape(83, 113)
    ndvi_data_year[:, :, i] = _ndvi_data_year.iloc[:, i].values.reshape(83, 113)
    temperature_data_year[:, :, i] = _temperature_data_year.iloc[:, i].values.reshape(83, 113)
    soil_moisture_data_year[:, :, i] = _soil_moisture_data_year.iloc[:, i].values.reshape(83, 113)

# 窗口大小列表
window_sizes = [5, 7, 9, 11, 13, 15, 17, 19, 21]
# 初始化相关系数DataFrame
correlation_dict = {}

for window_size in window_sizes:
    # 初始化相关系数矩阵(np.nan初始化)
    correlation_matrix = np.zeros((precip_data_year.shape[0], precip_data_year.shape[1], 3), dtype=np.float32)
    correlation_matrix[:] = np.nan

    # 对于每个窗口，计算斯皮尔曼相关系数
    for i in range(precip_data_year.shape[0] - window_size):
        for j in range(precip_data_year.shape[1] - window_size):
            # 提取窗口中的数据
            window_precipitation = precip_data_year[i:i + window_size, j:j + window_size, :]
            window_ndvi = ndvi_data_year[i:i + window_size, j:j + window_size, :]
            window_temperature = temperature_data_year[i:i + window_size, j:j + window_size, :]
            window_soil_moisture = soil_moisture_data_year[i:i + window_size, j:j + window_size, :]

            # 在窗口中的每个像素上计算相关系数
            corr_per_pixel = np.zeros((window_size, window_size, 3), dtype=np.float32)
            for k in range(window_size):
                for l in range(window_size):
                    corr_per_pixel[k, l, 0], _ = spearmanr(window_precipitation[k, l, :], window_ndvi[k, l, :])
                    corr_per_pixel[k, l, 1], _ = spearmanr(window_precipitation[k, l, :], window_temperature[k, l, :])
                    corr_per_pixel[k, l, 2], _ = spearmanr(window_precipitation[k, l, :], window_soil_moisture[k, l, :])

            # 计算窗口内的平均相关系数
            correlation_matrix[i, j, 0] = np.mean(corr_per_pixel[:, :, 0])
            correlation_matrix[i, j, 1] = np.mean(corr_per_pixel[:, :, 1])
            correlation_matrix[i, j, 2] = np.mean(corr_per_pixel[:, :, 2])

    # 将相关系数矩阵添加到correlation_matrices中
    correlation_dict['precipitation_ndvi_' + str(window_size)] = pd.Series(
        correlation_matrix[:, :, 0][~np.isnan(correlation_matrix[:, :, 0])].flatten())
    correlation_dict['precipitation_temperature_' + str(window_size)] = pd.Series(
        correlation_matrix[:, :, 1][~np.isnan(correlation_matrix[:, :, 1])].flatten())
    correlation_dict['precipitation_soil_moisture_' + str(window_size)] = pd.Series(
        correlation_matrix[:, :, 2][~np.isnan(correlation_matrix[:, :, 2])].flatten())
# 将相关系数矩阵保存到Excel文件中
df = pd.concat(correlation_dict, axis=1)
df.to_excel(r'E:\PRCP\table\window_corr\correlation_matrices.xlsx', index=False, sheet_name='年平均相关系数')

注意，建议运行时将窗口window_sizes的值进行编辑修改，由于我没有使用并行处理，所以如此多的窗口大小循环会导致运行时间长。

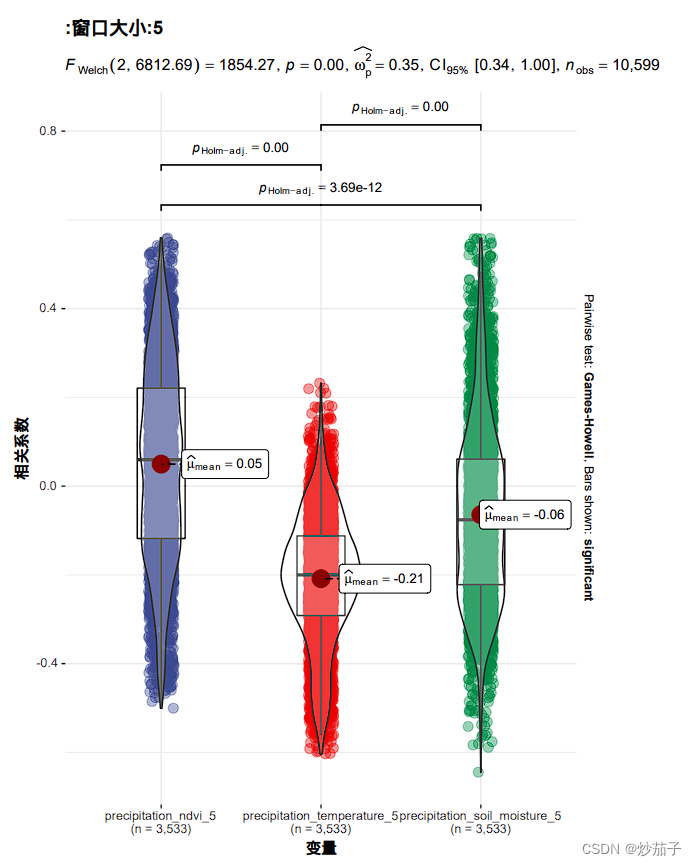
最后，我们将输出的excel数据进行小提琴图的绘制（只使用了其中窗口大小为5的数据进行绘制）：