一、概述
1.1概念
分支限界法是一种求解最优化问题的算法,常以广度优先或以最小耗费(最大效益)优先的方式搜索问题的解空间树。其基本思想是把问题的可行解展开,再由各个分支寻找最佳解。
在分支限界法中,分支是使用广度优先策略,依次生成扩展结点的所有分支。限界是在结点扩展过程中,计算结点的上界,搜索的同时剪掉某些分支。
1.2与回溯法区别
求解目标不同
- 回溯法是找出满足约束条件的所有解
- 分支限界法是找出满足条件的一个解,或某种意义下的最优解
搜索方式不同
- 回溯法:深度优先
- 分支限界法:广度优先或最小耗费优先
1.3分类
队列式分支限界法
将活结点表组织成一个队列,并按队列的先进先出原则选取下一个结点为当前扩展结点。
优先队列式分支限界法
将活结点表组织成一个优先队列,并按优先队列中规定的结点优先级选取优先级最高的下一个结点为当前扩展结点。
- 最大优先队列:使用最大堆,体现最大效益优先
- 最小优先队列:使用最小堆,体现最小费用优先
二、相关问题
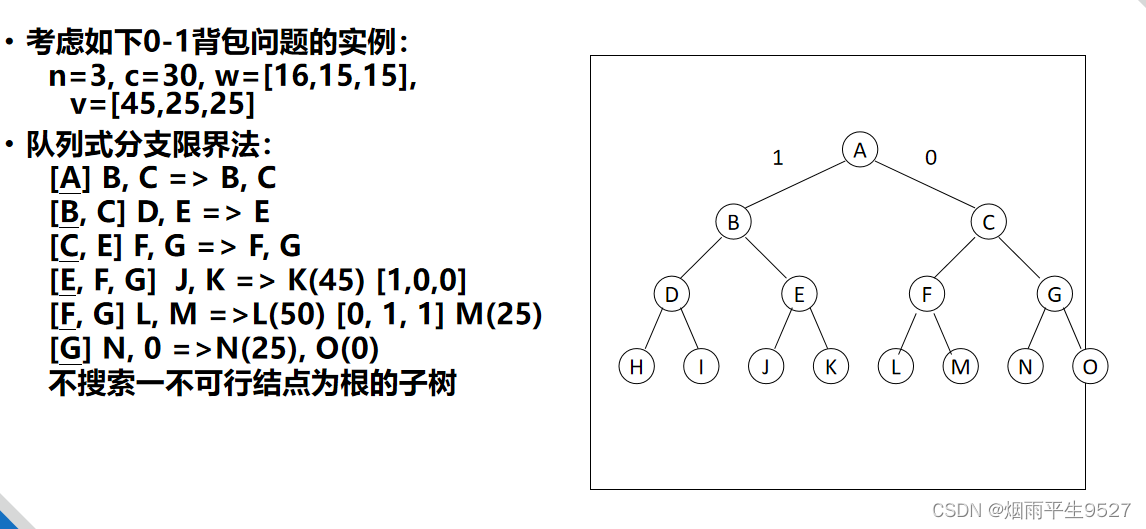
2.1 0-1背包问题
问题描述
- 给定n种物品和一个背包。物品i的重量是wi,其价值为vi,背包的容量为c。
- 应如何选择装入背包的物品,使得装入背包中物品的总价值最大?
- 在选择装入背包的物品时,对每种物品i只有2种选择,即装入背包或不装入背包。不能将物品i装入背包多次,也不能只装入部分的物品i。
队列式分支限界法
背包的容量c是30,图解如下:
#include<queue>
#include<iostream>
#include<vector>
#include<cstdio>
#include<string.h>
#include<algorithm>
#define N 100
using namespace std;
//记录物品信息
struct goods{
int wight;//物品重量
int value;//物品价值
};
//记录各节点信息
struct Node{
int lv;//记录当前节点层数
int wei;//当前总重量
int val;//当前总价值
int status[N];//当前节点的物品状态数组 0/1
};
int n,bestValue,cv,cw,C;//物品数量,价值最大,当前价值,当前重量,背包容量
int final[N];//最终存储状态
struct goods goods[N];
int BranchBound(){
queue<Node> que;
Node n1={0,0,0,{0}};
que.push(n1);
while(!que.empty()){
Node nd;
nd=que.front();
int lv=nd.lv; //当前第几层,可以作为goods[]数组的索引
//如果是最后一层节点,
//1. 记录该节点的信息
//2. 弹出队列
//3. 并跳过循环
if(lv>=n){
if(nd.val>bestValue)
{
bestValue=nd.val;
for(int i=0;i<n;i++)
{
final[i]=nd.status[i];
}
}
que.pop();
continue;
}
//判断左孩子节点
//该节点重量加上 下一个物品
if(nd.wei+goods[lv].wight<=C)
{
//构造左孩子节点
Node mid = que.front();
mid.lv+=1;
mid.val+=goods[lv].value;
mid.wei+=goods[lv].wight;
//置左孩子结点的 下一状态位为1
mid.status[lv]=1;
//将左孩子入队
que.push(mid);
}
//构造并加入右孩子节点
Node mid2 = que.front();
mid2.status[lv]=0;
mid2.lv+=1;
que.push(mid2);
//将当前访问节点弹出
que.pop();
}
return bestValue;
}
int main()
{
printf("物品种类n:");
scanf("%d",&n);
printf("背包容量C:");
scanf("%d",&C);
for(int i = 0; i < n; i++){
printf("物品%d的重量w[%d]及其价值v[%d]:",i+1,i+1,i+1);
scanf("%d%d",&goods[i].wight,&goods[i].value);
}
int sum3 = BranchBound();
printf("回溯法求解0/1背包问题:\nX=[");
for(int i = 0; i < n; i++)
cout << final[i] <<" ";//输出所求X[n]矩阵
printf("] 装入总价值%d\n",sum3);
return 0;
}
优先分支限界法
#include <iostream> // 引入输入输出流头文件
#include <queue> // 引入队列头文件
#include <vector> // 引入向量头文件
#include <algorithm> // 引入算法头文件
using namespace std; // 使用标准命名空间
// 物品结构体
struct Item {
int weight; // 物品的重量
int value; // 物品的价值
};
// 节点结构体
struct Node {
int level; // 节点的层次
int profit; // 节点的收益
int weight; // 节点的重量
int bound; // 节点的上界
vector<bool> taken; // 节点所选取的物品序列
};
// 优先队列的比较函数
struct CompareNode {
bool operator()(const Node& a, const Node& b) {
return a.bound < b.bound; // 按照上界从大到小排序
}
};
// 计算节点的上界
int calculateBound(Node u, int n, int c, vector<Item>& items) {
if (u.weight >= c) // 如果节点重量超过背包容量,返回0
return 0;
int profitBound = u.profit; // 初始化上界为节点收益
int j = u.level + 1; // 从下一层开始考虑物品
int totalWeight = u.weight; // 初始化总重量为节点重量
while ((j < n) && (totalWeight + items[j].weight <= c)) { // 当物品未考虑完且总重量不超过背包容量时,循环执行
totalWeight += items[j].weight; // 将物品加入总重量
profitBound += items[j].value; // 将物品价值加入上界
j++; // 考虑下一个物品
}
if (j < n) // 如果还有物品未考虑完,按照单位价值比例加入上界
profitBound += (c - totalWeight) * items[j].value / items[j].weight;
return profitBound; // 返回上界值
}
// 优先队列式分支限界法解决0-1背包问题
int knapsack(int n, int c, vector<int>& w, vector<int>& vv) {
vector<Item> items(n); // 创建一个物品向量
for (int i = 0; i < n; i++) { // 遍历输入的重量和价值向量,将其转化为物品结构体存入物品向量中
items[i].weight = w[i];
items[i].value = vv[i];
}
sort(items.begin(), items.end(), [](const Item& a, const Item& b) {
return (double)a.value / a.weight > (double)b.value / b.weight;
}); // 按照单位价值从大到小对物品向量进行排序
priority_queue<Node, vector<Node>, CompareNode> PQ; // 创建一个优先队列,用于存储节点
Node u, v; // 定义两个节点变量,u为当前节点,v为扩展节点
u.level = -1; // 初始化u的层次为-1,表示根节点之前的虚拟节点
u.profit = 0; // 初始化u的收益为0
u.weight = 0; // 初始化u的重量为0
int maxProfit = 0; // 初始化最大收益为0
u.bound = calculateBound(u, n, c, items); // 计算u的上界值
PQ.push(u); // 将u压入优先队列中
while (!PQ.empty()) { // 当优先队列不为空时,循环执行
u = PQ.top(); // 取出优先队列中的第一个元素,即上界最大的节点,赋值给u
PQ.pop(); // 弹出优先队列中的第一个元素
if (u.bound > maxProfit) { // 如果u的上界大于当前最大收益,说明有可能找到更优解,继续扩展子节点,否则剪枝处理
v.level = u.level + 1; // 将v的层次设为u的下一层,即考虑下一个物品是否放入背包中
v.weight = u.weight + items[v.level].weight; // 将v的重量设为u的重量加上当前考虑物品的重量,即假设放入背包中的情况
v.profit = u.profit + items[v.level].value; // 将v的收益设为u的收益加上当前考虑物品的价值,即假设放入背包中的情况
v.taken = u.taken; // 将v所选取的物品序列设为u所选取的物品序列,即继承父节点的选择情况
v.taken.push_back(true); // 在v所选取的物品序列末尾添加true,表示当前考虑物品被放入背包中
if (v.weight <= c && v.profit > maxProfit)
maxProfit = v.profit;
/* 如果v的重量不超过背包容量且v的收益大于当前最大收益,
则将最大收益更新为v的收益,即找到了一个更优解 */
v.bound = calculateBound(v, n, c, items);
/* 计算v的上界值 */
if (v.bound > maxProfit)
PQ.push(v);
/* 如果v的上界大于当前最大收益,
则将v压入优先队列中,等待后续扩展 */
v.weight = u.weight;
/* 将v的重量设为u的重量,即假设不放入背包中的情况 */
v.profit = u.profit;
/* 将v的收益设为u的收益,即假设不放入背包中的情况 */
v.taken = u.taken;
/* 将v所选取的物品序列设为u所选取的物品序列,
即继承父节点的选择情况 */
v.taken.push_back(false);
/* 在v所选取的物品序列末尾添加false,
表示当前考虑物品没有被放入背包中 */
v.bound = calculateBound(v, n, c, items);
/* 计算v的上界值 */
if (v.bound > maxProfit)
PQ.push(v);
/* 如果v的上界大于当前最大收益,
则将v压入优先队列中,等待后续扩展 */
}
}
return maxProfit;
/* 返回最大收益值 */
}
int main() {
int n = 3;
/* 定义物品数量为3 */
int c = 30;
/* 定义背包容量为30 */
vector<int> w = {16, 15, 15};
/* 定义一个向量存储每个物品的重量 */
vector<int> v = {45, 21, 25};
/* 定义一个向量存储每个物品的价值 */
int maxProfit = knapsack(n, c, w, v);
/* 调用背包函数,并将返回值赋给maxProfit变量 */
cout << "最大价值为:" << maxProfit << endl;
return 0;
}
2.2旅行售货员问题
问题描述:
某售货员要到若干城市去推销商品,已知各城市之间的路程,他要选定一条从驻地出发,经过每个城市一遍,最后回到住地的路线,使总的路程最短
结果为: 1 3 2 4
队列式分支限界法

#include <iostream>
#include <queue>
#include <vector>
using namespace std;
const int INF = 1e9;
struct Node {
vector<int> path; // 当前路径
vector<bool> visited; // 记录节点是否已访问
int cost; // 当前路径的总代价
int level; // 当前节点的层级
Node(int n) {
visited.resize(n, false);
cost = 0;
level = 0;
}
Node(const Node& other) {
path = other.path;
visited = other.visited;
cost = other.cost;
level = other.level;
}
};
void printSolution(const vector<int>& path) {
cout << "最优解是: [";
for (int i = 0; i < path.size(); i++) {
cout << path[i] + 1;
if (i != path.size() - 1) {
cout << " ";
}
}
cout << "]" << endl;
}
int tsp(vector<vector<int>>& graph, vector<int>& optimalPath) {
int n = graph.size();
// 初始化最小代价
int minCost = INF;
// 创建初始节点
Node rootNode(n);
rootNode.path.push_back(0); // 起始节点为0
rootNode.visited[0] = true;
rootNode.level = 1;
// 创建队列并将初始节点加入
queue<Node> q;
q.push(rootNode);
// 遍历队列中的节点
while (!q.empty()) {
Node currNode = q.front();
q.pop();
// 如果当前节点是叶子节点
if (currNode.level == n) {
// 加上回到起始节点的代价
currNode.cost += graph[currNode.path.back()][0];
// 更新最小代价和最优路径
if (currNode.cost < minCost) {
minCost = currNode.cost;
optimalPath = currNode.path;
}
}
// 遍历当前节点的邻居节点
for (int i = 0; i < n; i++) {
if (!currNode.visited[i] && graph[currNode.path.back()][i] != -1) {
// 创建新节点
Node newNode = currNode;
newNode.visited[i] = true;
newNode.path.push_back(i);
newNode.cost += graph[currNode.path.back()][i];
newNode.level = currNode.level + 1;
// 如果当前路径的代价小于最小代价,则加入队列继续搜索
if (newNode.cost < minCost) {
q.push(newNode);
}
}
}
}
return minCost;
}
int main() {
int n;
cin >> n;
// 读取输入的图
vector<vector<int>> graph(n, vector<int>(n));
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
cin >> graph[i][j];
}
}
// 求解旅行售货员问题
vector<int> optimalPath;
int minCost = tsp(graph, optimalPath);
// 输出结果
cout << "最优值为: " << minCost << endl;
printSolution(optimalPath);
return 0;
}
优先队列式分支限界法

#include <iostream>
#include <queue>
#include <vector>
using namespace std;
const int INF = 1e9;
struct Node {
vector<int> path; // 当前路径
vector<bool> visited; // 记录节点是否已访问
int cost; // 当前路径的总代价
int level; // 当前节点的层级
Node(int n) {
visited.resize(n, false);
cost = 0;
level = 0;
}
Node(const Node& other) {
path = other.path;
visited = other.visited;
cost = other.cost;
level = other.level;
}
};
struct CompareNode {
bool operator()(const Node& node1, const Node& node2) {
return node1.cost > node2.cost; // 按照代价从小到大排序
}
};
void printSolution(const vector<int>& path) {
cout << "最优解是: [";
for (int i = 0; i < path.size(); i++) {
cout << path[i] + 1;
if (i != path.size() - 1) {
cout << " ";
}
}
cout << "]" << endl;
}
int tsp(vector<vector<int>>& graph, vector<int>& optimalPath) {
int n = graph.size();
// 初始化最小代价
int minCost = INF;
// 创建初始节点
Node rootNode(n);
rootNode.path.push_back(0); // 起始节点为0
rootNode.visited[0] = true;
rootNode.level = 1;
// 创建优先队列并将初始节点加入
priority_queue<Node, vector<Node>, CompareNode> pq;
pq.push(rootNode);
// 遍历优先队列中的节点
while (!pq.empty()) {
Node currNode = pq.top();
pq.pop();
// 如果当前节点是叶子节点
if (currNode.level == n) {
// 加上回到起始节点的代价
currNode.cost += graph[currNode.path.back()][0];
// 更新最小代价和最优路径
if (currNode.cost < minCost) {
minCost = currNode.cost;
optimalPath = currNode.path;
}
}
// 遍历当前节点的邻居节点
for (int i = 0; i < n; i++) {
if (!currNode.visited[i] && graph[currNode.path.back()][i] != -1) {
// 创建新节点
Node newNode = currNode;
newNode.visited[i] = true;
newNode.path.push_back(i);
newNode.cost += graph[currNode.path.back()][i];
newNode.level = currNode.level + 1;
// 如果当前路径的代价小于最小代价,则加入优先队列继续搜索
if (newNode.cost < minCost) {
pq.push(newNode);
}
}
}
}
return minCost;
}
int main() {
int n;
cin >> n;
// 读取输入的图
vector<vector<int>> graph(n, vector<int>(n));
for (int i = 0; i < n; i++) {
for (int j = 0; j <n; j++) {
cin >> graph[i][j];
}
}
// 求解旅行售货员问题
vector<int> optimalPath;
int minCost = tsp(graph, optimalPath);
// 输出结果
cout << "最优值为: " << minCost << endl;
printSolution(optimalPath);
return 0;
}
2.3装载问题
问题描述:
最优装载问题:有一批n个集装箱要装上1艘载重量为C的轮船,其中集装箱i的重量为wi,在不考虑集装箱体积的情况下,如何选择装入轮船的集装箱,使得装入轮船中集装箱的总重量最大
已知最优装载问题的一个实例,n=3,C=30,W={16,15,15},试回答如下问题:
队列式分支限界法
#include <iostream>
#include <queue>
#include <vector>
using namespace std;
struct Node {
vector<int> load; // 当前装载情况
int level; // 当前节点的层级
int weight; // 当前装载的总重量
Node(int n) {
load.resize(n, 0);
level = 0;
weight = 0;
}
Node(const Node& other) {
load = other.load;
level = other.level;
weight = other.weight;
}
};
void knapsack(int n, int C, const vector<int>& weights) {
// 初始化最优值和最优解
int bestValue = 0;
vector<int> bestLoad(n, 0);
// 创建初始节点
Node rootNode(n);
rootNode.level = 0;
// 创建队列并将初始节点加入
queue<Node> q;
q.push(rootNode);
// 遍历队列中的节点
while (!q.empty()) {
Node currNode = q.front();
q.pop();
// 如果当前节点是叶子节点
if (currNode.level == n) {
// 更新最优值和最优解
if (currNode.weight <= C && currNode.weight > bestValue) {
bestValue = currNode.weight;
bestLoad = currNode.load;
}
continue;
}
// 不装载第level物品的子节点
Node noNode = currNode;
noNode.level = currNode.level + 1;
q.push(noNode);
// 装载第level物品的子节点
if (currNode.weight + weights[currNode.level] <= C) {
Node yesNode = currNode;
yesNode.level = currNode.level + 1;
yesNode.load[currNode.level] = 1;
yesNode.weight += weights[currNode.level];
q.push(yesNode);
}
}
// 输出结果
cout << "最优值为: " << bestValue << endl;
cout << "最优解为: [";
for (int i = 0; i < n; i++) {
cout << bestLoad[i] << " ";
}
cout << "]" << endl;
}
int main() {
int n, C;
cin >> n >> C;
// 读取物品重量
vector<int> weights(n);
for (int i = 0; i < n; i++) {
cin >> weights[i];
}
// 求解最优装载问题
knapsack(n, C, weights);
return 0;
}
优先队列式分支限界法 
#include <iostream>
#include <queue>
#include <vector>
using namespace std;
struct Node {
vector<int> load; // 当前装载情况
int level; // 当前节点的层级
int weight; // 当前装载的总重量
Node(int n) {
load.resize(n, 0);
level = 0;
weight = 0;
}
Node(const Node& other) {
load = other.load;
level = other.level;
weight = other.weight;
}
};
struct NodeComparator {
bool operator()(const Node& a, const Node& b) {
return a.weight < b.weight; // 按照节点的权重(装载的总重量)升序排序
}
};
void knapsack(int n, int C, const vector<int>& weights) {
// 初始化最优值和最优解
int bestValue = 0;
vector<int> bestLoad(n, 0);
// 创建初始节点
Node rootNode(n);
rootNode.level = 0;
// 创建优先队列并将初始节点加入
priority_queue<Node, vector<Node>, NodeComparator> pq;
pq.push(rootNode);
// 遍历优先队列中的节点
while (!pq.empty()) {
Node currNode = pq.top();
pq.pop();
// 如果当前节点是叶子节点
if (currNode.level == n) {
// 更新最优值和最优解
if (currNode.weight <= C && currNode.weight > bestValue) {
bestValue = currNode.weight;
bestLoad = currNode.load;
}
continue;
}
// 不装载第level物品的子节点
Node noNode = currNode;
noNode.level = currNode.level + 1;
pq.push(noNode);
// 装载第level物品的子节点
if (currNode.weight + weights[currNode.level] <= C) {
Node yesNode = currNode;
yesNode.level = currNode.level + 1;
yesNode.load[currNode.level] = 1;
yesNode.weight += weights[currNode.level];
pq.push(yesNode);
}
}
// 输出结果
cout << "最优值为: " << bestValue << endl;
cout << "最优解为: [";
for (int i = 0; i < n; i++) {
cout << bestLoad[i] << " ";
}
cout << "]" << endl;
}
int main() {
int n, C;
cin >> n >> C;
// 读取物品重量
vector<int> weights(n);
for (int i = 0; i < n; i++) {
cin >> weights[i];
}
// 求解最优装载问题
knapsack(n, C, weights);
return 0;
}
6.4布线问题
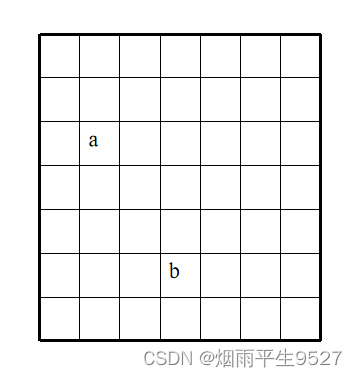
问题描述
印刷电路板将布线区域划分为n×m个方格阵列,如图所示。 精确的电路板布线问题要求确定连接方格a的中点到方格b的中点的最短布线方案。 布线时电路只能沿直线或直角布线。 为避免线路相交,已布线方格做上封闭标记,其他线路布线不允许穿过封闭区域。 为讨论方便,我们假定电路板外面的区域为已加封闭标记的方格。






![[Halcon3D] 主流的3D光学视觉方案及原理](https://img-blog.csdnimg.cn/3c6a3e0afc4940fca2c857b87d4dfe2b.png#pic_center)