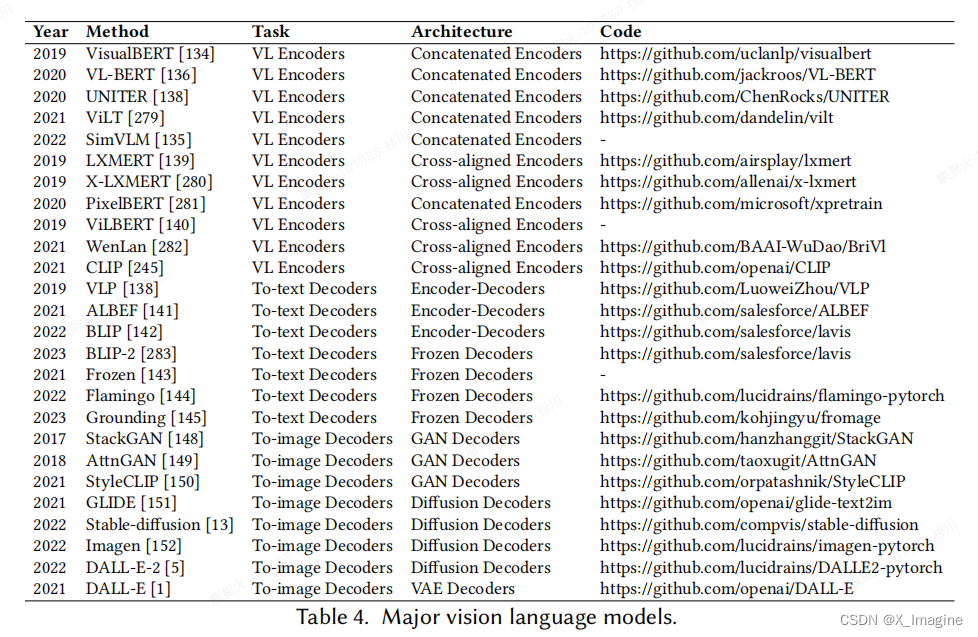
拉格朗日插值法是一种函数逼近方法，通过已知的数据点构建一个多项式函数，该函数能够恰好经过这些数据点。它可以用于插值，即根据给定的离散数据点推断出未知函数在其它点上的取值。拉格朗日插值法的优点是计算简单，容易理解和实现，但是由于多项式次数越高误差会越大，因此适用于较少的数据点，其定义如下

拉格朗日插值定理是秘密共享中的一种常用算法，可以将一个秘密分成多个部分，并分配给多个参与者。下面我们通过一个具体的实例来说明拉格朗日插值定理的运算过程。

假设有一个秘密 S，需要将其分成 4 部分，分别分配给 4 个参与者。我们先随机生成 4 个不同的 x 值，然后将它们作为拉格朗日插值定理中的插值点 (x, y)：

x	y
1	S1
2	S2
3	S3
4	S4

其中，S1、S2、S3 和 S4 分别表示分配给 4 个参与者的秘密部分。接下来，我们使用拉格朗日插值定理计算多项式 L(x)，并根据 L(x) 的系数来分配秘密部分。拉格朗日插值定理的计算公式如下：

在这个公式中，k 表示插值点的数量，xi​ 和 yi​ 分别表示第 i 个插值点的 x 和 y 值。

假设我们需要将秘密分成 4 部分，因此插值点的数量为 4。根据上表中的数据，我们可以得到：

其中，yi​ 表示对应的秘密部分，xi​ 表示第 i 个插值点的 x 值。这个多项式的系数即为各个参与者分配到的秘密部分。

例如，假设秘密 S 的值为 10，随机生成的 4 个 x 值为 1、2、3 和 5，则对应的 4 个 y 值为：

x	y
1	6
2	8
3	2
5	4

将这些值代入拉格朗日插值定理的公式中计算，可以得到多项式：

化简后可得：

这个多项式的系数即为各个参与者分配到的秘密部分。例如，参与者 1 可以获得 L(1) 的值，将其代入上面的多项式中，可以得到：

因此，参与者 1 获得的秘密部分为 6。 同样的方法，可以计算出其他参与者分配到的秘密部分。需要注意的是，拉格朗日插值定理只能保证在插值点处多项式与原函数相等，而在其他地方则不一定。因此，如果想要获得更高的安全性，需要使用更复杂的秘密共享算法。

学习导航：https://www.xqnav.top/