🔎选择题

(1)以下方法，哪个不是对add方法的重载?

public class Test
{
    public void add( int x,int y,int z){}
}

A.public int add(int x,int y,float z){return 0;}
B.public int add(int x,int y,int z){return 0;}
C.public void add(int x,int y){}
D.所有选项都不是

B

重载的特性

• 方法名相同
• 参数列表不同(参数的类型, 顺序, 个数)

(2)在Java中，关于HashMap类的描述，以下错误的是 ( )

A.HashMap使用键/值得形式保存数据
B.HashMap能够保证其中元素的顺序
C.HashMap允许将null用作键
D.HashMap允许将null用作值

B

(3)在Java中，( ) 类提供定位本地文件系统，对文件或目录及其属性进行基本操作

A.FileInputStream
B.FileReader
C.FileWriter
D.File

D

A. 输入字节流
B. 读取文件
C. 写入文件

(4)下面程序的运行结果是 ( )

String str1 = "hello";
String str2 = "he" + new String("llo");
System.err.println(str1 == str2);

A.true
B.false
C.exception
D.无输出

B

str2 是字符串拼接后的结果, 等同于 new String(“hello”)
str2 的内容是 “hello”, 但是地址与 str1 的地址不同, 因此运行结果为 false

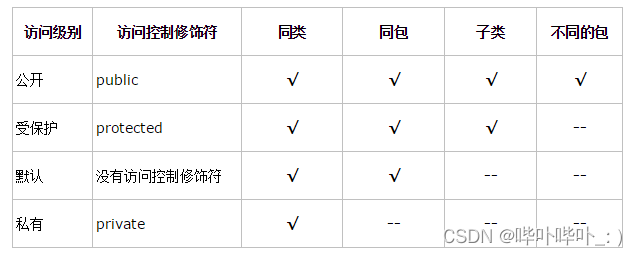
(5)下列哪个修饰符可以使在一个类中定义的成员变量只能被同一包中的类访问？

A.private
B.无修饰符
C.public
D.protected

B

图片来自网络

(6)Java接口的方法修饰符可以为？(忽略内部接口)

A.private
B.protected
C.final
D.abstract

D

接口中的方法默认是要被实现的
接口中的方法的修饰符默认为 public abstract

(7)下列程序的运行结果 ( )

public void getCustomerInfo() {
        try {
            // do something that may cause an Exception
        } catch (java.io.FileNotFoundException ex) {
            System.out.print("FileNotFoundException!");
        } catch (java.io.IOException ex) {
            System.out.print("IOException!");
        } catch (java.lang.Exception ex) {
            System.out.print("Exception!");
        }
}

A.IOException!
B.IOException!Exception!
C.FileNotFoundException!IOException!
D.FileNotFoundException!IOException!Exception!

A

catch() 一次只能捕获一个异常
B, C, D. 捕获到了多个异常

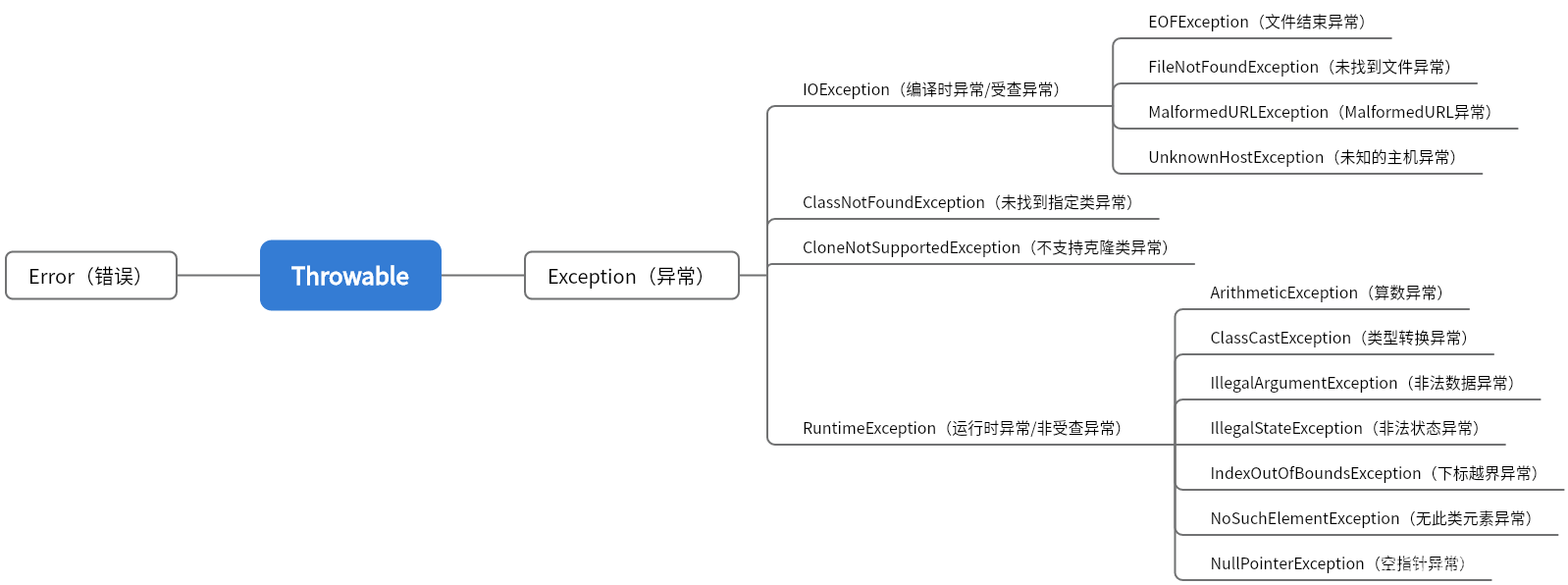
(8)下列哪种异常是检查型异常，需要在编写程序时声明？

A.NullPointerException
B.ClassCastException
C.FileNotFoundException
D.IndexOutOfBoundsException

C

A.空指针异常
B.类型转换异常
D.下标越界异常

(9)选项中哪一行代码可以添加到题目中而不产生编译错误？

public abstract class MyClass {
     public int constInt = 5;
     //add code here
     public void method() {
     }
}

A.public abstract void method(int a);
B.constInt = constInt + 5;
C.public int method();
D.public abstract void anotherMethod() {}

A

B. 不能在类内方法外执行该操作(可以在方法内部执行)
C. 缺少方法体 { }
D. abstract 修饰的方法不能有方法体 { }

(10)如下代码，执行test()函数后，屏幕打印结果为（）

public class Test2 {
    public void add(Byte b) {
        b = b++;
    }
    public void test() {
        Byte a = 127;
        Byte b = 127;
        add(++a);
        System.out.print(a + " ");
        add(b);
        System.out.print(b + "");
    }
}

A.127 127
B.128 127
C.129 128
D.其他选项都不对

D

Byte 类型的数据表示的范围是 -128 ~ 127
a = 127, 调用 add(++a) 方法, a 的值变为 -128
b = 127, 调用 add(b++) 方法, b 的值变为 127
最终输出 -128 127

🔎编程题

🥝二进制插入

题目描述

给定两个32位整数n和m，同时给定i和j，将m的二进制数位插入到n的二进制的第j到第i位,保证n的第j到第i位均为零，且m的二进制位数小于等于i-j+1，其中二进制的位数从0开始由低到高。

解题思路

以 n = 1024, m = 19, j = 2, i = 6 举例

n 1024 的二进制位为 0100 0000 0000
m 19   的二进制位为 0000 0001 0011

• 保证 n 的第 j 到第 i 位均为零
  • 1024 的第 2 到第 6 位均为零
• m 的二进制数位小于等于 i - j + 1(6 - 2 + 1)
  • m 的二进制数位为 5, 小于等于 5

根据题意, 让 n | (m << j) 位即可

n 1024       的二进制位为 0100 0000 0000
m 19 << 2    的二进制位为 0000 0100 1100
n | (m << j) 的二进制位为 0100 0100 1100(1100)

public int binInsert(int n, int m, int j, int i) {
        // write code here
        return n | (m << j);
}

📢题目链接
链接: link

---

🥝查找组成一个偶数最接近的两个素数

题目描述

任意一个偶数（大于2）都可以由2个素数组成，组成偶数的2个素数有很多种情况，本题目要求输出组成指定偶数的两个素数差值最小的素数对。

数据范围：输入的数据满足 4≤n≤1000

输入描述

输入一个大于2的偶数

输出描述

从小到大输出两个素数

解题思路

根据题意模拟即可

素数指在大于1的自然数中，除了1和它本身以外不再有其他因数的自然数

//查找组成一个偶数最接近的两个素数
import java.util.Scanner;
public class Main {
    public static void main(String[] args) {
        Scanner scan = new Scanner(System.in);
        int x = scan.nextInt();
		// i >= 2, 最小的素数是2 
        for (int i = x / 2; i >= 2; i--) {
            if (isPrime(i) && isPrime(x - i)) {
                System.out.println(i);
                System.out.println(x - i);
                return;
            }
        }
    }

    //判断是否为素数
    private static boolean isPrime(int num) {
        for (int i = 2; i <= Math.sqrt(num); i++) {
            if (num % i == 0) return false;
        }
        return true;
    }

}

📢题目链接
链接: link

---

🔎结尾

创作不易,如果对您有帮助,希望您能点个免费的赞👍
大家有什么不太理解的，可以私信或者评论区留言，一起加油