大家好呀，我是一个SLAM方向的在读博士，深知SLAM学习过程一路走来的坎坷，也十分感谢各位大佬的优质文章和源码。随着知识的越来越多，越来越细，我准备整理一个自己的激光SLAM学习笔记专栏，从0带大家快速上手激光SLAM，也方便想入门SLAM的同学和小白学习参考，相信看完会有一定的收获。如有不对的地方欢迎指出，欢迎各位大佬交流讨论，一起进步。

SLAM是一个定位问题，定位问题就离不开刚体运动的表达和传感器和全局坐标系之间的相互转换，下面我们来一起学习一下。

目录

1. 刚体位姿的表达

1.1. 变换矩阵

1.2. 旋转向量和欧拉角

1.3. 四元数

1.4 相关代码

2. 刚体位姿优化

2.1 李群

2.2 李群与李代数 

 2.3 指数与对数映射

2.4 求导与扰动模型

2.5 Sophus李群李代数计算

1. 刚体位姿的表达

1.1. 变换矩阵

        变换矩阵由旋转矩阵和平移矩阵构成，用来表述刚体在三维空间的运动。在三维空间中的任何一种变换都可以用一个旋转矩阵和一个平移矩阵来表示。

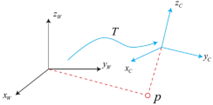
 表达式如下所示，其中R为旋转矩阵，t为平移矩阵，T为变换矩阵。

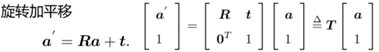
在SLAM中，4x4变换矩阵通常用于表示相机或机器人在三维空间中的姿态变换。这种变换矩阵通常称为齐次变换矩阵（Homogeneous Transformation Matrix），它由以下组成部分构成：

旋转矩阵（Rotation Matrix）：3x3的旋转矩阵表示物体的旋转姿态。它描述了相机或机器人在空间中的方向变化。

平移向量（Translation Vector）：3维向量表示物体从一个位置平移到另一个位置的平移量。它描述了相机或机器人在空间中的位置变化。

齐次坐标（Homogeneous Coordinates）：齐次坐标是为了方便表示平移和旋转而引入的一种扩展坐标系统。通过将3维坐标扩展为4维，可以用一个4维向量来表示平移和旋转。齐次坐标通常用于将平移和旋转合并到一个矩阵中。 

                                            R11 R12 R13 T1
                                            R21 R22 R23 T2
                                            R31 R32 R33 T3
                                              0      0      0    1

其中，R11到R33是3x3的旋转矩阵，描述了物体的旋转姿态；T1到T3是平移向量，描述了物体的位置变化。最后一行是[0 0 0 1]，用于保持齐次坐标的一致性。

1.2. 旋转向量和欧拉角

从变换矩阵可以看到，变换矩阵用16个变量，表达了6自由度，比较麻烦，求解困难。所以想寻求一种更为简单的表达方式，便引入了欧拉角，欧拉角( Euler Angles)将旋转分解为三个方向上的转动例，按Z-Y-X顺序转动轴可以是定轴或动轴，顺序亦可不同常见的有 : yaw-pitch-roll，这样表达旋转参数量大大减少。

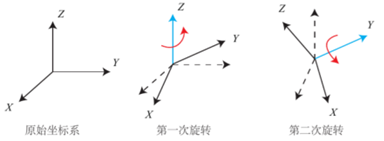
但欧拉角有一个严重的问题是万向锁问题：第一次随便绕一个轴旋转一定角度，第二次绕第二个轴旋转90°，第三次绕最后一个轴旋转的效果与绕第一个轴相同。以扭头形象的举例子，身体转向代表绕x轴旋转，昂首俯首代表绕y轴旋转，头向左右肩膀歪头代表绕z轴旋转。首先将身体随意旋转一定角度，接着昂首90°即看向天花板，随后保证面一直朝向天花板歪头任意角度，则会发现此时歪头和身体转向的效果相同，出现了奇异性。并且理论上可以证明，用3个实数来描述旋转问题都会出现奇异性问题，因为这个问题，欧拉角不适用与插值或者迭代。 

1.3. 四元数

旋转矩阵用9个量描述3自由度旋转具有冗余性，欧拉角虽然紧凑但存在奇异性，所以需要寻求一种新的旋转描述方式。

• 复数

复数最直观的理解就是旋转，4*i*i=-4；就是“4”在数轴上旋转了180度。那么4*i就是旋转了90度。

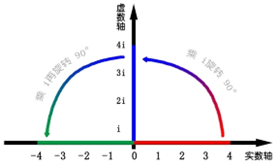
复数域定义如下，对应了复数的平面坐标系称为复平面，x轴和y轴分别称为实轴和虚轴。当r等于1时称为单位复数。 

 特别的我们拿i乘以一个复数，对应的几何意义是旋转90°

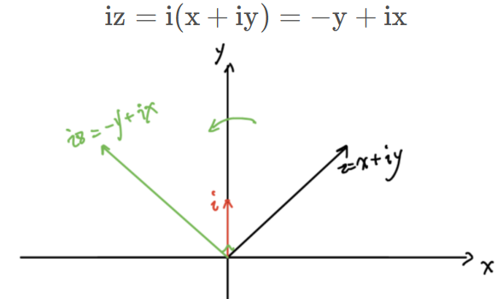
在知道了可以用复数表达旋转后，引入了四元数

四元数：三维情况下，四元数可作为复数的扩充，具有三个虚部和一个实部。四元数相比于角轴、欧拉角的优势：紧凑、无奇异性。且四元数与角轴之间可以相互转换。

1.4 相关代码

矩阵基本运算（代码lidar_slam_course/ch3/eigen/useEigen）

• 安装Eigen

Sudo apt-get install libeigen3-dev

• Eigen矩阵线性代数库常用函数
• 编译运行

mkdir ./build
cd build
cmake ..
make
./eigenMatrix

• 旋转向量、欧拉角、四元数相互转换

（代码lidar_slam_course/ch3/eigen/useGeomety）

• 坐标变换小例子

（代码lidar_slam_course/ch3/eigen/examples/coordinateTransform）

• 位姿可视化小例子

（代码lidar_slam_course/ch3/eigen/examples/plotTrajectory）

• 可视化位姿各种表达方式，左侧对应旋转矩阵、平移矩阵、欧拉角和四元数

（代码lidar_slam_course/ch3/eigen/visualizeGeometry）

2. 刚体位姿优化

2.1 李群

上面介绍过怎么表达位姿的变化，一个合适的表达是为了更方便的求解优化。而求解优化的过程常常需要求最小值，用到求导运算，那么如何方便快速的求导矩阵是一个问题。

2.2 李群与李代数 

可以看到李群没有加法，意味着不能够定义导数求导，所以需要找到一个与之对应的且能够加法的形式。对于任意旋转矩阵有：

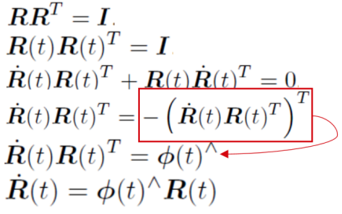
说明在t=0附近，R可求解。给定某时刻的R即求一个Φ与之对应。即为SO(3)对应的李代数so(3)。每个李群都有与之对应的李代数。李代数描述了李群单位元附近的正切空间性质。指数相乘底数不变，指数相加，李群和李代数成为了乘法与加法转变的桥梁。

 2.3 指数与对数映射

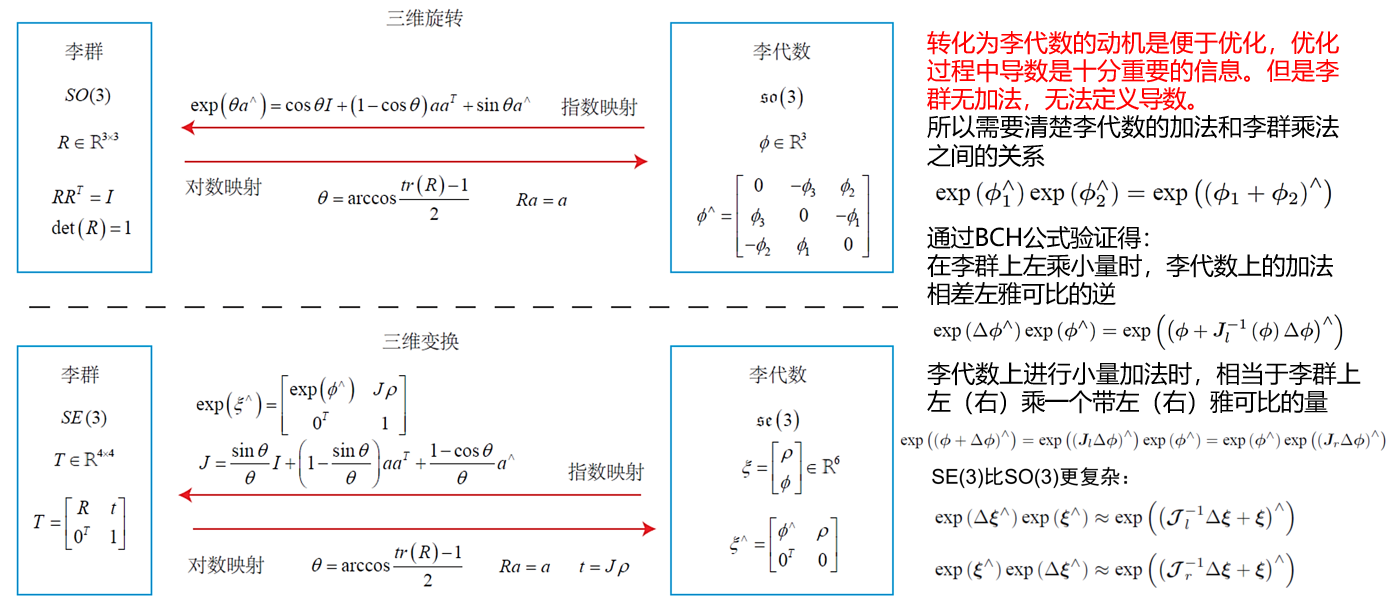
2.4 求导与扰动模型

扰动模型求解更加简洁，避免了求雅可比矩阵。通过李群和李代数定义了运动变换的导数，就可以进行优化求解了。

2.5 Sophus李群李代数计算

Sophus依赖eigen和fmt库，所以首先安装这俩库。

• Eigen

sudo apt-get install libeigen3-dev

• fmt库

git clone GitHub - fmtlib/fmt: A modern formatting library
cd fmt
mkdir build
cd build
cmake ..
make
sudo make install

• Sophus库

git clone GitHub - strasdat/Sophus: C++ implementation of Lie Groups using Eigen.
cd sophus
mkdir build
cd build
cmake ..
make
sudo make install

由旋转矩阵构建李群、李代数并进行指数对数映射

（代码lidar_slam_course/ch3/sophus/SOSEsose）

评估轨迹误差

（代码lidar_slam_course/ch3/sophus/example）

到此，你知道了刚体运动的表达和求导方式，有了这些基础就可以进行位姿的求解优化了。前面的Ubunru、ROS、编译、点云、位姿优化的基础终于铺垫差不多了，下一节将讲解如何求解SLAM问题。