1 N维数组对象（ndarray）
先理解如何通过numpy进行批次计算：
引入numpy，随机生成数组：
import numpy as np
data=np.random.randn(2,3)
print(data)
print(data*10)
print(data+data)
[[ 0.88001557 -0.70682337 0.81193788]
[ 1.46063048 -1.10190869 -1.28097833]]
[[ 8.80015573 -7.0682337 8.11937877]
[ 14.6063048 -11.01908691 -12.80978327]]
[[ 1.76003115 -1.41364674 1.62387575]
[ 2.92126096 -2.20381738 -2.56195665]]
ndarray是⼀个通⽤的同构数据多维容器，也就是说，其中的所有元素必须是相同类型的。每个数组都有⼀个shape（⼀个表示各维度⼤⼩的元组）和⼀个dtype（⼀个⽤于说明数组数据类型的对象）：
print(data.shape)
print(data.dtype)
(2, 3)
float64
1.1 创建ndarray
使用array函数，可以将一个列表转换为数组形式：
import numpy as np
data=[1,1,2,1,0,0]
a1=np.array(data)
print(data)
print(a1)
[1, 1, 2, 1, 0, 0]
[1 1 2 1 0 0]
嵌套序列会被转换成一个多维数组：
import numpy as np
data=[[1,1,1,1],[2,2,2,2]]
a1=np.array(data)
print(data)
print(a1)
[[1, 1, 1, 1], [2, 2, 2, 2]]
[[1 1 1 1]
[2 2 2 2]]
zeros和ones分别可以创建指定⻓度或形状的全0或全1数组。empty可以
创建⼀个没有任何具体值的数组，返回的是一些未初始化的垃圾值。
import numpy as np
data1=np.zeros((3,6))
data2=np.ones((4,4))
data3=np.empty((2,6))
print(data1)
print(data2)
print(data3)
[[0. 0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0. 0.]]
[[1. 1. 1. 1.]
[1. 1. 1. 1.]
[1. 1. 1. 1.]
[1. 1. 1. 1.]]
[[1.32306018e-311 2.47032823e-322 0.00000000e+000 0.00000000e+000
8.01097888e-307 2.42336543e-057]
[5.20269970e-090 1.65847383e-076 1.53471495e-052 5.53922725e+174
3.99910963e+252 1.69105613e-306]]
一些数组创建函数：
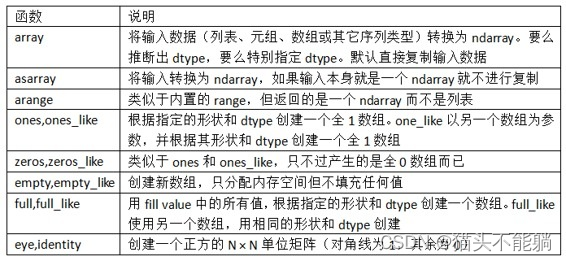
1.2 numpy支持的数据类型
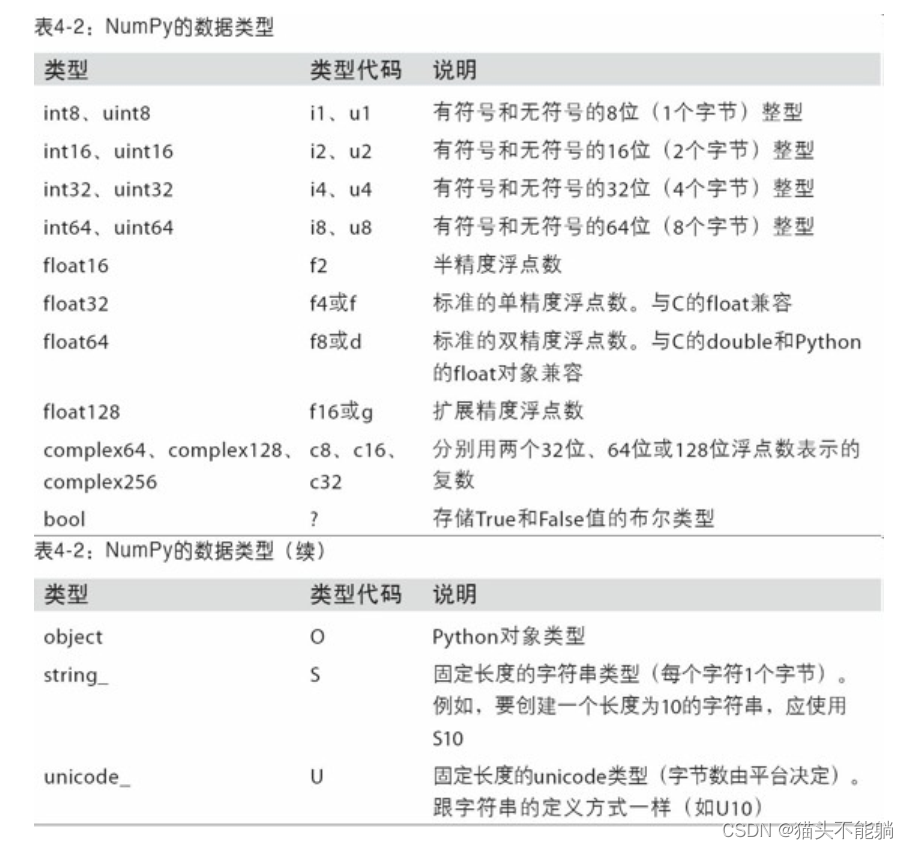
通过ndarray的astype方法可以转换数组的数据类型：
import numpy as np
data1=np.array([1,2,3,4,5])
print(data1.dtype)
data1_=data1.astype(np.float64)
print(data1_.dtype)
int32
float64
1.3 基本索引与切片
一维数组：
import numpy as np
data=np.arange(10)
print(data)
print(data[5])
print(data[5:8])
data[5:8]=12
print(data)
[0 1 2 3 4 5 6 7 8 9]
5
[5 6 7]
[ 0 1 2 3 4 12 12 12 8 9]
当创建一个切片以后，数据不会被复制，关于切片的任何修改都会直接反映到源数组上：
import numpy as np
data=np.arange(10)
print(data)
data_slice=data[5:9]
print(data_slice)
data_slice[1]=12345
print(data)
data_slice[:]=88
print(data)
[0 1 2 3 4 5 6 7 8 9]
[5 6 7 8]
[ 0 1 2 3 4 5 12345 7 8 9]
[ 0 1 2 3 4 88 88 88 88 9]
如果你想要得到的是ndarray切⽚的⼀份副本⽽⾮视图，就需要明确地进⾏复制操作，例如arr[5:8].copy()。
二维数组：
import numpy as np
data2w=np.array([[1,2,3],[4,5,6],[7,8,9],[10,11,12]])
print(data2w)
print(data2w[1]) #索引第2个数组
print(data2w[0][2])#索引第1个数组的第3个值
print(data2w[0,2])#索引第1个数组的第3个值,上面的等价形式
[[ 1 2 3]
[ 4 5 6]
[ 7 8 9]
[10 11 12]]
[4 5 6]
3
3
多维数组
import numpy as np
data3w=np.array([[[1,2,3],[4,5,6]],[[7,8,9],[10,11,12]]])#2*2*3的三维数组
print(data3w)
print('--------------------')
x=data3w[0]#2*3的二维数组
print(x)
print('--------------------')
y=data3w[1,1]#第2个二维数组的第2个一维数组
print(y)
[[[ 1 2 3]
[ 4 5 6]]
[[ 7 8 9]
[10 11 12]]]
--------------------
[[1 2 3]
[4 5 6]]
--------------------
[10 11 12]
切片索引
一维：
import numpy as np
data=np.array([0,1,2,3,4,5,6,7,8,9])
print(data[1:6])
[1 2 3 4 5]
二维：
import numpy as np
data=np.array([[0,1,2],
[3,4,5],
[6,7,8]])#3*3的二维数组
print(data[:2])
[[0 1 2]
[3 4 5]]
它是沿着第0轴（即第⼀个轴）切⽚的。也就是说，切⽚是沿着⼀个轴向选取元素的。表达式data[:2]可以被认为是“data的前两⾏”。
可以⼀次传⼊多个切⽚，就像传⼊多个索引那样：
import numpy as np
data=np.array([[0,1,2],
[3,4,5],
[6,7,8]])#3*3的二维数组
print(data[:2,1:])
[[1 2]
[4 5]]
可以选取第⼆⾏的前两列，还可以选择第三列的前两⾏：
import numpy as np
data=np.array([[0,1,2],
[3,4,5],
[6,7,8]])#3*3的二维数组
print(data[1,:2])
print("--------------------------")
print(data[:2,2])
[3 4]
--------------------------
[2 5]
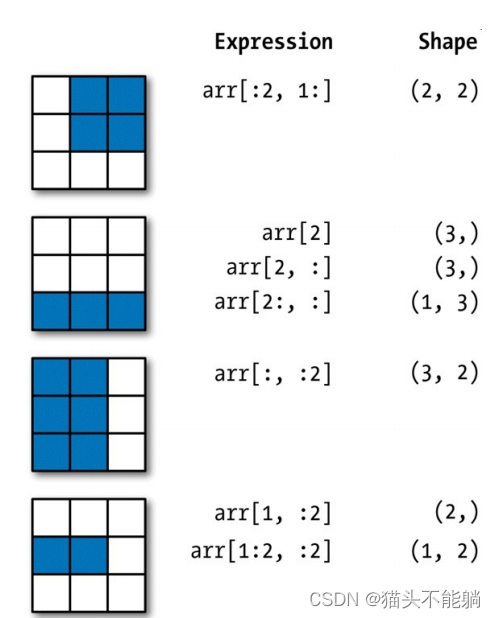
1.4 数组转置
转置
import numpy as np
data=np.arange(15).reshape((3,5))
print(data)
data=data.T
print(data)
[[ 0 1 2 3 4]
[ 5 6 7 8 9]
[10 11 12 13 14]]
[[ 0 5 10]
[ 1 6 11]
[ 2 7 12]
[ 3 8 13]
[ 4 9 14]]
在进⾏矩阵计算时，经常需要⽤到该操作，⽐如利⽤np.dot计算矩阵内积：
x=np.dot(data.T,data)
print(x)
[[ 30 80 130]
[ 80 255 430]
[130 430 730]]
2 通用函数
2.1 ⼀元（unary）ufunc
sqrt和exp：
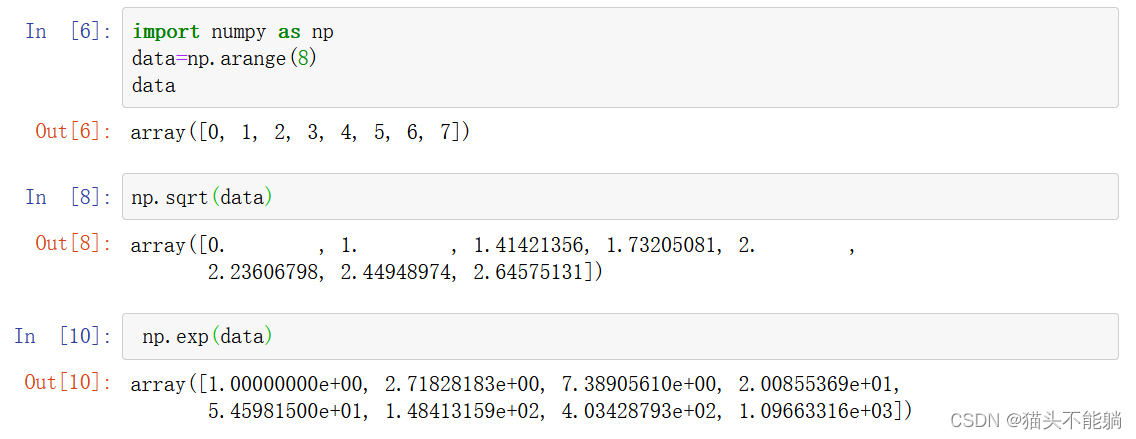
2.2 ⼆元（binary）ufunc
numpy.maximum计算了x和y中元素级别最⼤的元素
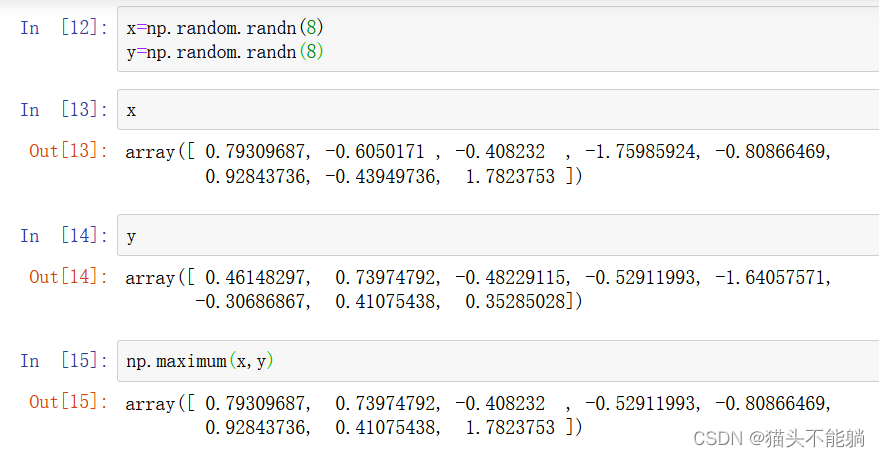
3 利⽤数组进⾏数据处理
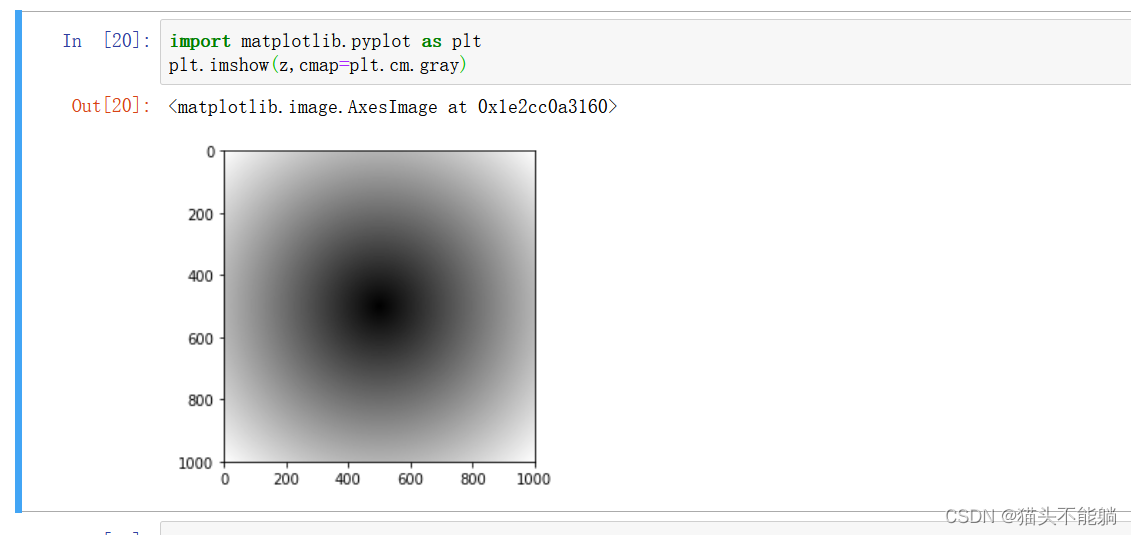
假设我们想要在⼀组值（⽹格型）上计算函数的平方和再开根号，
np.meshgrid函数接受两个⼀维数组，并产⽣两个⼆维矩阵（对应于两个数组中所有的(x,y)对）：
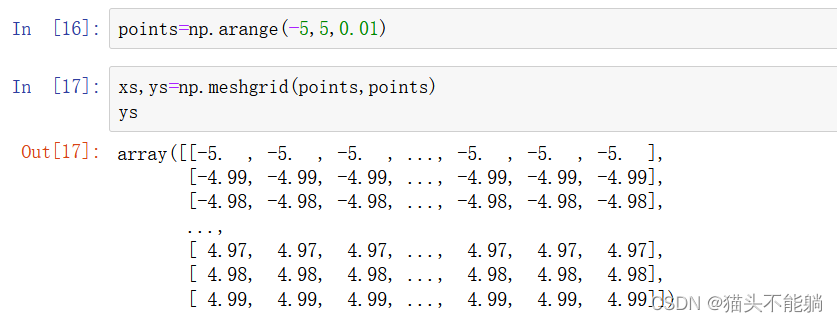把这两个数组当做两个浮点数那样编写表达式即可：
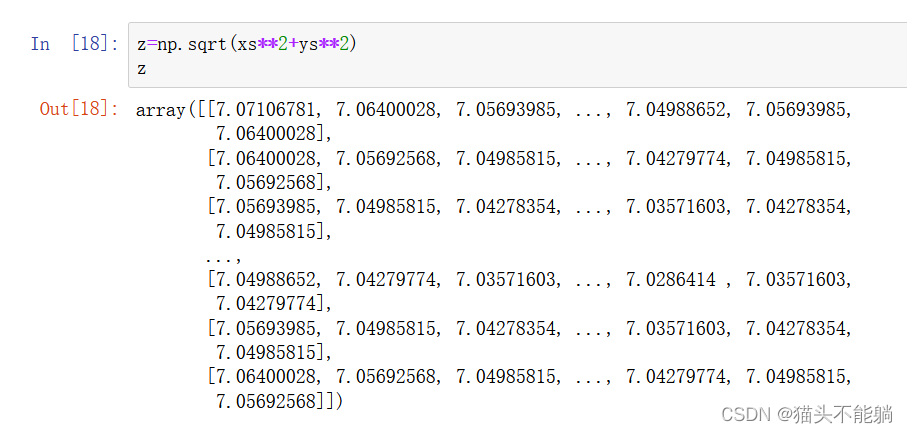
3.1 将条件逻辑表述为数组运算
numpy.where函数是三元表达式x if condition else y的⽮量化版本。
np.where的第⼆个和第三个参数不必是数组，它们都可以是标量值。在数据分析⼯作中，where通常⽤于根据另⼀个数组⽽产⽣⼀个新的数组。假设有⼀个由随机数据组成的矩阵，你希望将所有正值替换为2，将所有负值替换为－2。若利⽤np.where，则会⾮常简单：
import numpy as np
data=np.random.randn(4,4)
print(data)
data=data>0
print(data)
x=np.where(data>0,2,-2)
print(x)
[[ 0.96352433 -1.6204806 0.14904115 1.23612457]
[ 0.00931106 -0.52504499 -0.64019292 -0.58209492]
[ 1.01209682 -0.20559156 1.50025012 0.03056071]
[ 0.95015428 -0.21081623 -2.74972977 -1.8681938 ]]
[[ True False True True]
[ True False False False]
[ True False True True]
[ True False False False]]
[[ 2 -2 2 2]
[ 2 -2 -2 -2]
[ 2 -2 2 2]
[ 2 -2 -2 -2]]
传递给where的数组⼤⼩可以不相等，甚⾄可以是标量值。
3.2数学和统计方法
4 线性代数
NumPy提供了⼀个⽤于矩阵乘法的dot函数（既是⼀个数组⽅法也是numpy命名空间中的⼀个函数）：
x.dot(y)等价于np.dot(x, y)：
import numpy as np
x=np.array([[1,2,3],[4,5,6]])
y=np.array([[6,1],[7,4],[8,5]])
print(x)
print("----------------")
print(y)
m=x.dot(y)
print("----------------")
print(m)
n=np.dot(x,y)
print("----------------")
print(n)
[[1 2 3]
[4 5 6]]
----------------
[[6 1]
[7 4]
[8 5]]
----------------
[[ 44 24]
[107 54]]
----------------
[[ 44 24]
[107 54]]
numpy.linalg中有⼀组标准的矩阵分解运算以及诸如求逆和⾏列式之类的东⻄：
5 伪随机数生成
