引言

---

💡 作者简介：专注于C/C++高性能程序设计和开发，理论与代码实践结合，让世界没有难学的技术。包括C/C++、Linux、MySQL、Redis、TCP/IP、协程、网络编程等。
👉
🎖️ CSDN实力新星，社区专家博主
👉
🔔 专栏介绍：从零到c++精通的学习之路。内容包括C++基础编程、中级编程、高级编程；掌握各个知识点。
👉
🔔 专栏地址：C++从零开始到精通
👉
🔔 博客主页：https://blog.csdn.net/Long_xu

---

🔔 上一篇：【005】C++数据类型之实型（浮点数）、有符号数以及无符号数

一、进制的概述

• 二进制：0~1，以0b开头，bitset< 8 >输出。
• 八进制：0~7，以0开头，oct输出。
• 十进制：0~9，以数字开头，cout默认输出十进制。
• 十六进制：0 ~ 9和A ~ F，以0x开头，hex输出，不区分正负。
• n进制：0~n-1。

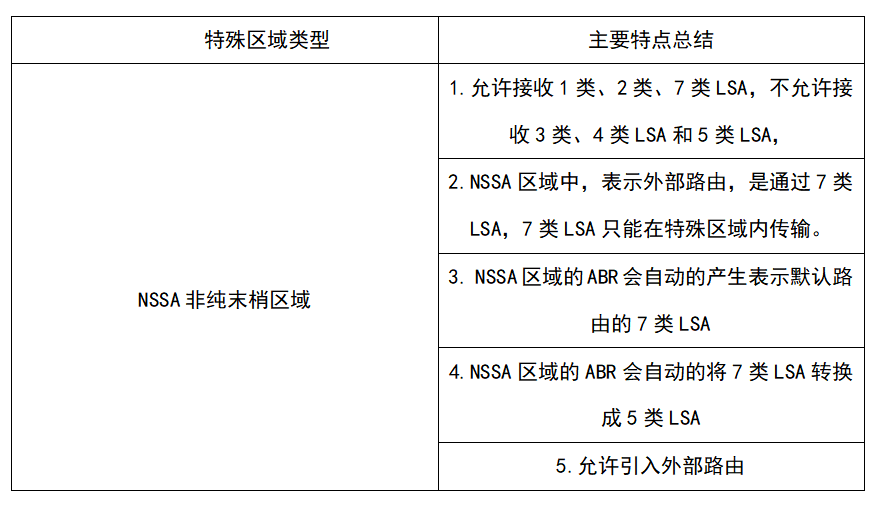
二、十进制转二进制、八进制、十六进制（短除法）

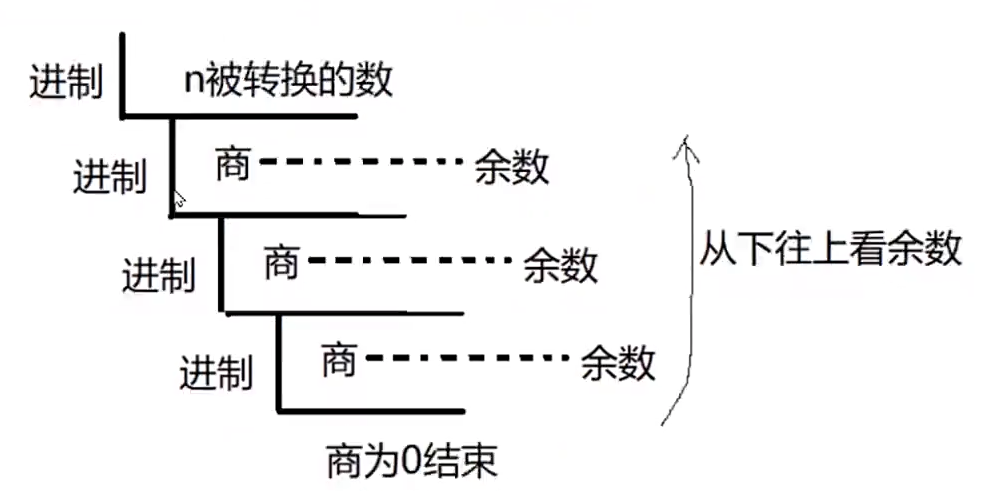
示例1：123转二进制，得0b0111 1011。
示例2：123转八进制，得0173。
示例3：123转十六进制，得0x7B。

通用算法：

void DecimalToOtherNumbers(int num,int other, char b[], int maxlen)
{
	memset(b, 0, maxlen);
	int n = num;
	if (num < 0)
		n = 0 - num;
	if (maxlen <= 0)
		return;
	int sum = n / other;
	int len = 0;
	while (sum != 0)
	{
		if (len >= maxlen)
			break;
		if (n % other>10)
		{
			b[len] = n % other + 'A'-10;
		}
		else
			b[len] = n % other + '0';
		n /= other;
		sum = n / other;
		len++;
	}
	b[len] = n % other + '0';

	// 现在是倒序的，需要对调位置,使其符合阅读习惯
	int idx = 0;
	while (idx < len)
	{
		int tmp = b[idx];
		b[idx] = b[len];
		b[len] = tmp;
		idx++;
		len--;
	}
}

三、二进制、八进制、十六进制转十进制（位次幂）

转换公式：

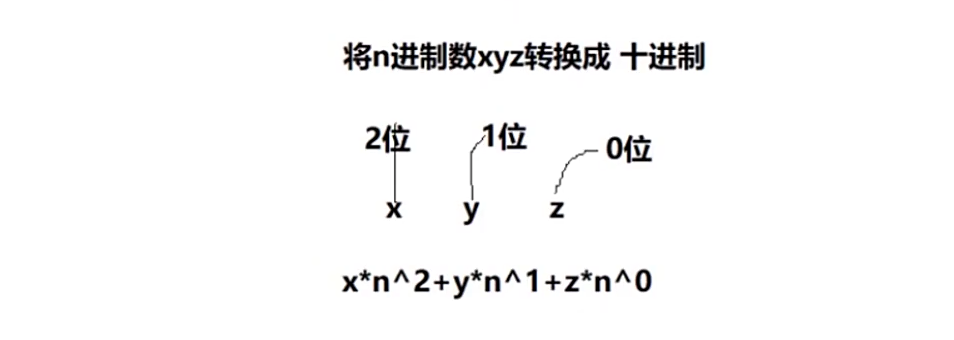
示例1：二进制0b11000011转为二进制，$1\times 2^7+1\times 2^6+0\times 2^5+0\times 2^4+0\times 2^3+0\times 2^2+1\times 2^1+1\times 2^0=195$。

示例2：将八进制数0123转换为十进制，$1\times 8^2+2\times 8^1+3\times 8^0=83$。

示例3：将十六进制0x12转为十进制，$1\times 16^1+2\times 16^0=18$。

四、其他进制间的转换

4.1、二进制转八进制

从右往左，每3位二进制对应1位八进制。

1101 1010
11 011 010
3 3 2

所以二进制1101 1010转八进制就是0332。

4.2、二进制转十六进制

从右往左，每4位二进制对应1位十六进制。

1101 1010
D ----- A

所以二进制1101 1010转十六进制就是0xDA。

4.3、八进制转二进制

一位八进制对应三位二进制。

0123
001 010 011
0101 0011

所以八进制0123的二进制就是0101 0011。

4.4、十六进制转二进制

一位十六进制对应四位二进制。

0x123
0001 0010 0011

所以十六进制0x123的二进制就是0001 0010 0011。

4.5、八进制转十六进制

八进制先转为二进制，再从二进制转为十六进制。没有直接方式。

八进制 --> 二进制 --> 十六进制
0123 --> 0101 0011 --> 0x53

4.6、十六进制转八进制

十六进制先转为二进制，再从二进制转为八进制。没有直接方式。

十六进制 --> 二进制 --> 八进制
0x12 --> 0001 0010 --> 022

4.7、注意

不同进制仅仅是数据的不同表现形式而已。
示例：

#include <iostream>
#include <bitset>

using namespace std;

int main()
{
	int num=100;
	cout<<"num的二进制："<<bitset<8>(num)<<endl;
	cout<<"num的八进制："<<oct<<num<<endl;
	cout<<"num的十进制："<<dec<<num<<endl;
	cout<<"num的十六进制："<<hex<<num<<endl;
	return 0;
}

输出：

总结

C++ 中常见的数字进制有十进制、二进制、八进制、十六进制。转换这些进制可以使用以下方法：

1. 从十进制转换到其他进制：

• 二进制：使用除以 2 取余数的方法，将得到的余数倒序排列即为二进制。
• 八进制：使用除以 8 取余数的方法，将得到的余数倒序排列即为八进制。
• 十六进制：使用除以 16 取余数的方法，将得到的余数转换为对应的字母或数字，倒序排列即为十六进制。

2. 从其他进制转换到十进制：

• 二进制：将每一位数乘以对应的权重（2 的 n 次方），再将结果相加即可得到十进制。
• 八进制：将每一位数乘以对应的权重（8 的 n 次方），再将结果相加即可得到十进制。
• 十六进制：将每一位数转换为对应的十进制数，乘以对应的权重（16 的 n 次方），再将结果相加即可得到十进制。

3. 从一个进制转换到另一个进制：
   先将原数转换为十进制，再将十进制转换为目标进制。

例如，将十进制数 42 转换为二进制：
42 / 2 = 21 … 0
21 / 2 = 10 … 1
10 / 2 = 5 … 0
5 / 2 = 2 … 1
2 / 2 = 1 … 0
1 / 2 = 0 … 1
得到的余数倒序排列即为二进制数 101010。