- 张量方法的引入
- 自然法则与坐标无关,坐标系的引入方便分析,但也掩盖了物理本质
- 指标符号
- 哑标和自由标
- Einstein求和约定:凡在某一项内,重复一次且仅重复一次的指标,表示对该指标在它的取值范围内求和,并称这样的指标为哑指标。
- 凡在同一项内不重复出现的指标为自由标
- 同一个方程中各项自由标必须相同
- 不能改变某一项的自由标,但所有项的自由标可以改变
- Einstein求和约定:凡在某一项内,重复一次且仅重复一次的指标,表示对该指标在它的取值范围内求和,并称这样的指标为哑指标。
- 克罗内克(Kronecker-δ)符号
例如:
常见性质:
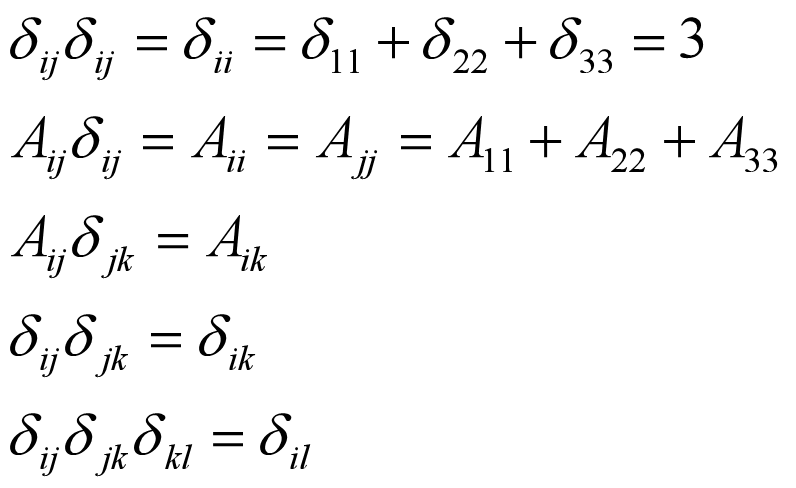
- Ricci 符号
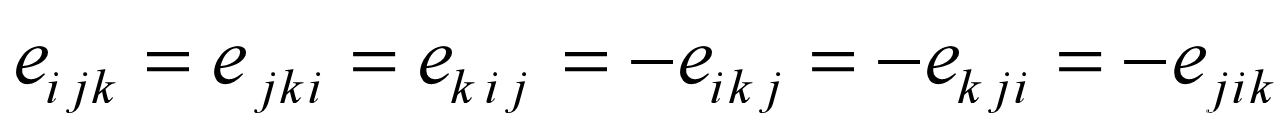
- e-δ恒等式

 其他重要等式
其他重要等式
- e-δ恒等式
矢量的基本运算
点积
![]()
叉积
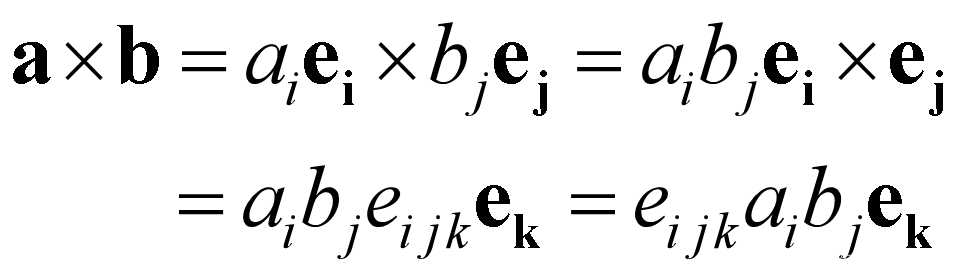
混合积
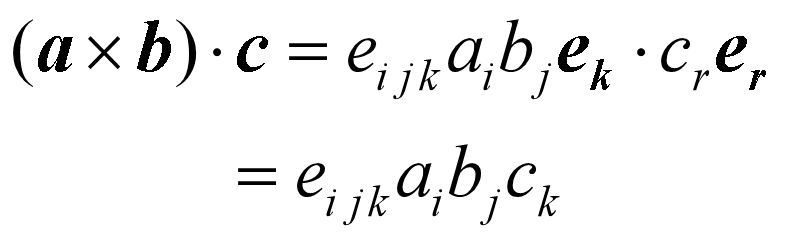
并矢
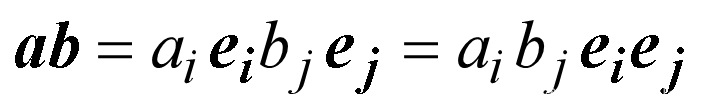
坐标变换与张量的定义
- 平面笛卡儿坐标系旋转变换
- 张量定义:在坐标变换时,满足如下变换关系的量称为张量

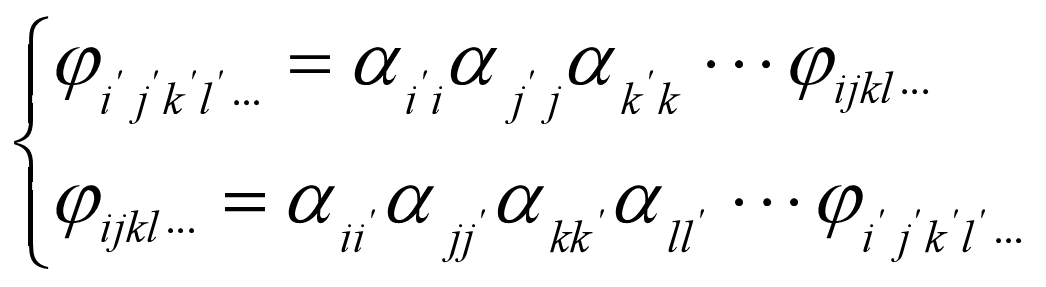
- 可写成下式的量也称为张量

张量代数
![]()
加减法
- 只有同阶张量才能加减,仍为同阶张量
矢量与张量的点积
- 点乘得到的新张量比原张量低一阶
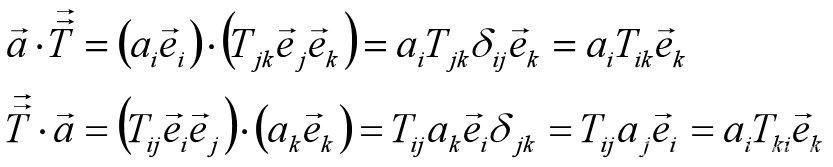
矢量与张量的叉积
- 叉乘得到的新张量与原张量同阶
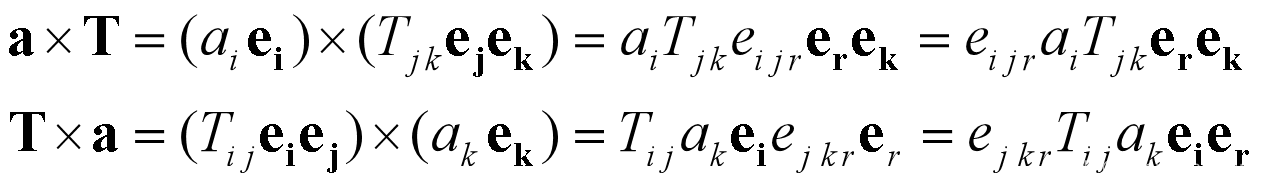
张量与张量的点积
- 两个张量点积的结果仍为张量。新张量的阶数是原两个张量的阶数之和减2。

张量的双点积

张量的双叉乘
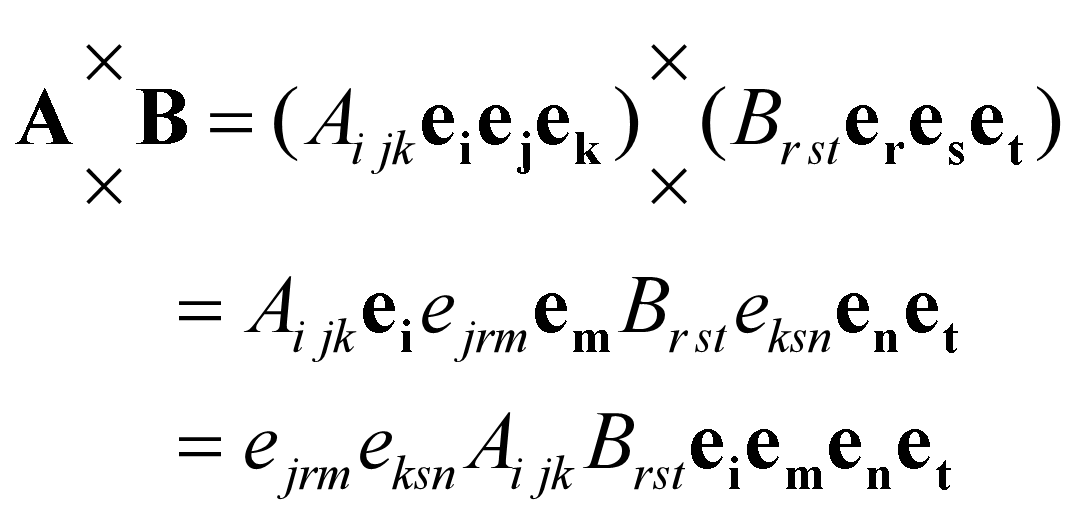
张量缩并
- 进行缩并:将其中的二个基矢量点乘,得到比原张量低二阶的新张量。二阶张量相当于将对角元素求和。
- 张量代数的商法则是指当两个张量空间之间的同态映射存在时,我们可以定义一个商空间,并在该空间中定义一个张量积。这种定义允许我们通过将一个张量空间中的元素等价于另一个张量空间中的元素,来将一个张量空间划分成等价类。在商空间中,我们将两个商元素的张量积定义为它们代表的等价类中的两个未经缩并的张量的张量积的等价类。这样,我们可以通过定义商张量空间来处理彼此之间有联系的张量空间。
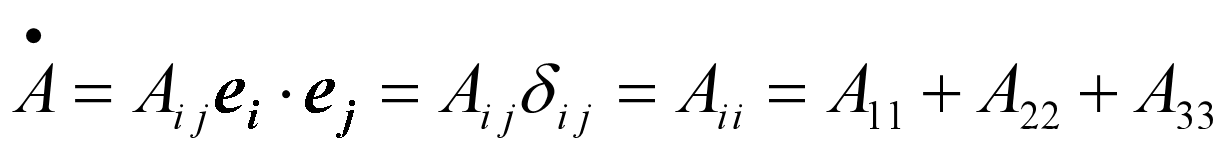
指标置换
- 若对该张量的分量中任意两个指标交换次序,得到一个与原张量同阶的新张量。
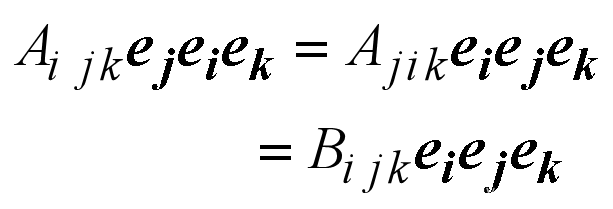
对称化和反称化
- 对于二阶张量:
- 对称,有6个独立分量
- 反对称,有3个独立分量
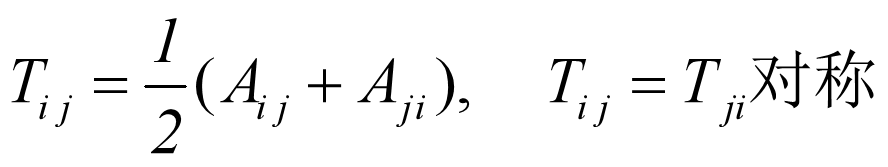
![]()
- 高阶张量:
- 关于(指标,指标)对称的?阶张量/反对称张量
商法则
- 张量代数的商法则是指当两个张量空间之间的同态映射存在时,我们可以定义一个商空间,并在该空间中定义一个张量积。这种定义允许我们通过将一个张量空间中的元素等价于另一个张量空间中的元素,来将一个张量空间划分成等价类。在商空间中,我们将两个商元素的张量积定义为它们代表的等价类中的两个未经缩并的张量的张量积的等价类。这样,我们可以通过定义商张量空间来处理彼此之间有联系的张量空间。
二阶张量(仿射量)
- 二阶张量相当于一个方矩阵,在向量空间有类似线性变换算子的作用。
- 是线性算子
转置
略
逆
略
对称仿射量的主向和主值
- 对于仿射量B,若存在三个相互垂直的方向i,j,k,其映象 B\cdot i,B\cdot j,B\cdotk也相互垂直,则称该三个方向为B的主向。
- 对称仿射量T必存在三个主向和三个相应的主值。
- 主值S满足特征方程:

- 其中,Ⅰ,Ⅱ,Ⅲ称为仿射量T的第一、第二、第三不变量
 |  | 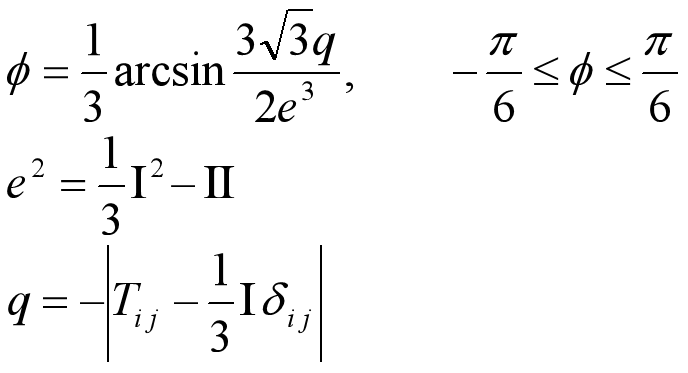 |
各向同性张量
- 在坐标任意变换时,各分量保持不变的张量,称为各向同性张量。
- 零阶张量(标量)总是各向同性的。
- 一阶张量(矢量)总不是各向同性的。
- 对称二阶张量其三个主值相等与其各向同性等价。
张量分析
梯度、散度、旋度
- Hamilton算子
- Hamilton算子相当于一阶张量
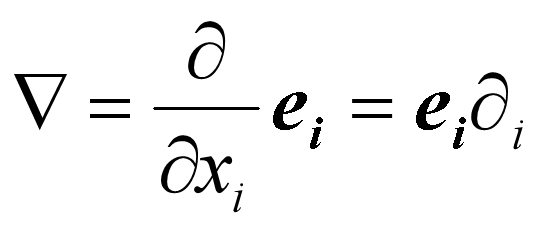
容许变换
- 容许变换被用来表示在不同坐标系下的张量,而不是在一个特定的坐标系中。这在应用中非常有用,因为在不同坐标系中对于同一个物理问题的描述是常见的。通过使用容许变换,张量可以在不同的坐标系中转换,以便分析和处理。
- 在计算机图形学中,容许变换常用于表示三维物体在不同的观察角度下的变化。这种类型的变换可以通过一个矩阵来实现,称为旋转矩阵。旋转矩阵可以用来描述平面和立体图形的旋转、缩放和平移。
- 如下,依次有坐标变换和逆变换
![]()
![]()
- 满足以下两个条件的变换称之为容许变换
- 正逆变换函数均为单值连续可微函数
- 在域内任意点处:

度规张量
- 度规张量是描述空间度量的数学工具,在张量分析中非常重要。度规张量可以用来表示空间的内部结构和变形情况,也可以用来计算曲率、变形等量。
- 在三维欧几里得空间中,度规张量可以表示为一个对称的二阶张量。它的每一个分量对应于两个向量之间的夹角余弦值,因此可以用来测量向量之间的角度和长度。
- 度规张量还可以用来描述时空的性质。在相对论中,时空被视为四维弯曲的,度规张量可以用来描述这种弯曲的情况,进而推导出广义相对论的基本公式和方程。

![]() (度量张量,仅当i=j成立)
(度量张量,仅当i=j成立)
例如:球坐标系
矩阵导数
- 常数求导为常数零
- 线性算子
- 乘积法则

- 商法则
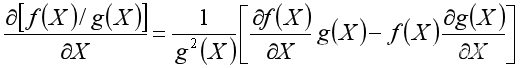
- 经验式1

- 经验式2
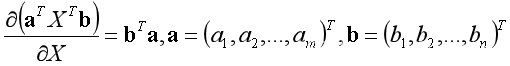
- 经验式3

- 经验式4