一文深度解读机器学习模型的评估方法

我们训练学习好的模型，通过客观地评估模型性能，才能更好实际运用决策。模型评估主要有：预测误差情况、拟合程度、模型稳定性等方面。还有一些场景对于模型预测速度（吞吐量）、计算资源耗用量、可解释性等也会有要求，这里不做展开。

一、评估预测误差情况

机器学习模型预测误差情况通常是评估的重点，它不仅仅是学习过程中对训练数据有良好的学习预测能力，根本上在于要对新数据能有很好的预测能力（泛化能力），所以我们常通过测试集的指标表现评估模型的泛化性能。

评估模型的预测误差常用损失函数作为指标来判断，如回归预测的均方损失。但除此之外，用损失函数作为评估指标有一些局限性且并不直观（如像分类任务的评估还常用f1-score，可以直接展现各种类别正确分类情况）。在此，我们主要对回归和分类预测任务分别解读其常用误差评估指标。

技术交流

技术要学会分享、交流，不建议闭门造车。一个人可以走的很快、一堆人可以走的更远。

好的文章离不开粉丝的分享、推荐，资料干货、资料分享、数据、技术交流提升，均可加交流群获取，群友已超过2000人，添加时最好的备注方式为：来源+兴趣方向，方便找到志同道合的朋友。

方式①、添加微信号：dkl88191，备注：来自CSDN + python
方式②、微信搜索公众号：Python学习与数据挖掘，后台回复：加群

1.1 回归任务的误差评估指标

评估回归模型的误差，比较简单的思路，可以对真实值与预测值的差异“取正”后求平均。如下：

均方误差（MSE）均方误差（MSE）为实际值与预测值的差值取平方求平均。其中y是实际值，y^ 是预测值

均方根误差（RMSE）

均方根误差（RMSE）是对MSE的开根号

平均绝对误差（MAE）

平均绝对误差（MAE）是预测值与真实值之间的误差取绝对值的平均

由于MAE用到了绝对值（不可导），很少用在训练的损失函数。用于最终评估模型还是可以的。

均方根对数误差(RMSLE)

上述指标的差异对比：

① 异常值敏感性：MAE也就是真实预测误差，而RMSE，MSE都有加平方，放大了较大误差样本的影响（对于异常值更敏感），如果遇到个别偏离程度非常大的离群点时，即便数量很少，也会让这两个指标变得很差。减少异常点的影响，可以采用RMSLE，它关注的是预测误差的比例，即便存在离群点，也可以降低这些离群点的影响。

② 量纲差异：不同于MSE做了平方，RMSE（平方后又开根号）及MAE对于原量纲是不变，会更直观些。而RMSE 与 MAE 的尽管量纲相同，RMSE比MAE实际会大一些。这是因为RMSE是先对误差进行平方的累加后再开方，也放大了误差之间的差距。

③ 跨任务的量纲差异问题：实际运用中，像RMSE、MAE是有个问题的，不同任务的量纲是会变的，比如我们预测股价误差是10元，预测房价误差是1w，跨越了不同任务我们就没法评估哪个模型效果更好。接下来介绍，R2分数指标，它对上面的误差进一步做了归一化，就有了统一的评估标准。

R^2分数

R^2分数常用于评估线性回归拟合效果时，其定义如下：

R^2分数可以视为我们模型的均方误差除以用实际值平均值作为预测值时的均方误差(像baseline模型)的比值。
这样，R^2分数范围被归约到了[0,1],当其值为0时，意味着我们的模型没有什么效果，和baseline模型那样猜的效果一致。当值为1，模型效果最好，意味着模型没有任何误差。

补充一点，当R^2值为0时且模型为线性回归时，也可以间接说明特征与标签没有线性关系。
这也是常用的共线性指标VIF的原理，分别尝试以各个特征作为标签，用其他特征去学习拟合，得到线性模型R^2值，算出VIF。VIF为1即特征之间完全没有共线性（共线性对线性模型稳定性及可解释性会有影响，工程上常用VIF<10作为阈值）。

1.2 分类模型的误差评估指标

对于分类模型的分类误差，可以用损失函数（如交叉熵。在分类模型中交叉熵比MSE更合适，简单来说，MSE无差别得关注全部类别上预测概率和真实概率的差。交叉熵关注的是正确类别的预测概率。）来评估：

但损失函数评估分类效果不太直观，所以，分类任务的评估还常用f1-score、precision、recall，可以直接展现各种类别正确分类情况。

precision、recall、f1-score、accuracy

准确率（accuracy）。即所有的预测正确（TP+TN）的占总数（TP+FP+TN+FN）的比例；

查准率P（precision）：是指分类器预测为Positive的正确样本（TP）的个数占所有预测为Positive样本个数（TP+FP）的比例；

查全率R（recall）：是指分类器预测为Positive的正确样本（TP）的个数占所有的实际为Positive样本个数（TP+FN）的比例。

F1-score是查准率P、查全率R的调和平均：

上述指标的总结：

① 综合各类别的准确度：准确率accuracy对于分类错误情况的描述是比较直接的，但是对于正负例不平衡的情况下，accuracy评价基本没有参考价值，比如欺诈用户识别的分类场景，有950个正常用户样本（负例），50个异常用户（正例），模型把样本都预测为正常用户样本，准确率是非常好的达到95%。但实际上是分类效果很差。accuracy无法表述出少数类别错误分类的情况，所以更为常用的是F1-score，比较全面地考量到了查准率与查全率。

② 权衡查准率与查全率：查准率与查全率常常是矛盾的一对指标，有时要结合业务有所偏倚低地选择“更准”或者“更全”（比如在欺诈用户的场景里面，通常偏向于对正例识别更多“更全”，尽管会有更高的误判。“宁愿错杀一百，也不放走一个”），这时可以根据不同划分阈值下的presion与recall曲线（P-R曲线），做出两者权衡。

kappa值

kappa是一个用于一致性检验的指标（对于分类问题，所谓一致性就是模型预测结果和实际分类结果是否一致）。kappa值计算也是基于混淆矩阵的，它一种能够**惩罚模型预测“偏向性”**的指标，根据kappa的计算公式，越不平衡的混淆矩阵（即不同类别预测准度的差异大），kappa值就越低。

其公式含义可解释为总准确度对比随机准确度的提升与完美模型对比随机准确度的提升的比值：

kappa取值为-1到1之间,通常大于0，可分为五组来表示不同级别的一致性：0.0_{0.20极低的一致性(slight)、0.21}0.40一般的一致性(fair)、0.41~0.60 中等的一致性(moderate)、0.61~0.80 高度的一致性(substantial) 和 0.81~1几乎完全一致(almost perfect)。

ROC曲线、AUC

ROC曲线（Receiver operating characteristic curve），其实是多个混淆矩阵的综合结果。如果在上述模型中我们没有固定阈值，而是将模型预测结果从高到低排序，将每个概率值依次作为动态阈值，那么就有多个混淆矩阵。

对于每个混淆矩阵，我们计算两个指标TPR（True positive rate）和FPR（False positive rate），TPR=TP/(TP+FN)=Recall 即召回率，FPR=FP/(FP+TN)，FPR即为实际负样本中，预测为正样本占比。最后，我们以FPR为x轴，TPR为y轴画图，就得到了ROC曲线。我们通过求解ROC曲线下的面积，也就是AUC(Area under Curve)，AUC可以直观的评价分类器的好坏，通常介于0.5和1之间，值越大越好。

对AUC指标的分析总结：

由于衡量ROC是“动态的阈值”，故AUC不依赖分类阈值，摆脱了固定分类阈值看分类效果的局限性。
ROC由不同阈值TPR、FPR绘制。更大的ROC面积（AUC）意味着较小的FPR下有更大的TPR，较小的FPR也就是较大的1-FPR = TN/(TN+FP)=TNR，所以AUC其实是TPR（也叫召回率、敏感度）与 TNR（也叫特异度）的综合考虑。
由混淆矩阵可以看出，AUC的TNR（即1-FPR）、TPR 和样本的实际好坏占比是无关的，它们都只关注相应实际类别的识别的全面度。（不像查准率precision是跨越了实际类别间情况做评估）。简单来说：AUC对样本的正负比例情况是不敏感，即使正例与负例的比例发生了很大变化，ROC曲线面积也不会产生大的变化
AUC是ROC曲线的面积，其数值的物理意义是：随机给定一正一负两个样本，将正样本预测分值大于负样本的概率大小。也就是，AUC是区分能力的“排序性”指标（正样本高于负样本的概率分值即可），对具体的判定概率不敏感——忽略了模型的拟合效果，而对于一个优秀的模型而言，我们期望的是正负样本的概率值是差异足够大的。举个栗子，模型将所有负样本预测为0.49，正样本预测为0.51，那这个模型auc即是1（但正负样本的概率很接近，一有扰动模型就预测错了）。而我们期望模型的预测好坏的间隔尽量大，如负样本预测为0.1以下，正样本预测为0.8以上，此时虽然auc一样，但这样的模型拟合效果更好，比较有鲁棒性。

AUC 对比 F1-score差异

AUC不依赖分类阈值，F1-score需指定阈值，不同阈值结果有差异；
当正负样本比例变化时，AUC影响不大，F1-score会有比较大影响（因为查准率precision是跨越了实际类别间情况做评估）；
两者有包含召回率（正样本识别全面度情况）并有兼顾到FP（负样本误识别为正样本情况），都要求了“全”与“准”的均衡。
F1-score可以通过阈值灵活地调节查全率、查准率不同侧重偏好。而AUC只能给一个笼统的信息。

# 上述指标可以直接调用 sklearn.metrics
from sklearn.metrics import precision_score, recall_score, f1_score, accuracy_score, roc_curve, auc, cohen_kappa_score,mean_squared_error
...
yhat = model.predict(x)

f1_score(y, yhat)

二、模型拟合程度

对于模型的拟合程度，常用欠拟合、拟合良好、过拟合来表述。通常，拟合良好的模型有更好泛化能力，在未知数据（测试集）有更好的效果。

我们可以通过训练及验证集误差（如损失函数）情况评估模型的拟合程度。从整体训练过程来看，欠拟合时训练误差和验证集误差均较高，随着训练时间及模型复杂度的增加而下降。在到达一个拟合最优的临界点之后，训练误差下降，验证集误差上升，这个时候模型就进入了过拟合区域。实践中的欠拟合通常不是问题，可以通过使用强特征及较复杂的模型提高学习的准确度。而解决过拟合，即如何减少泛化误差，提高泛化能力，通常才是优化模型效果的重点。对于解决过拟合，常用的方法在于提高数据的质量、数量以及采用适当的正则化策略。

三、模型稳定性

如果上线的模型不稳定，意味着模型不可控，影响决策的合理性。对于业务而言，这就是一种不确定性风险，这是不可接受的（特别对于厌恶风险的风控领域）。

我们通常用群体稳定性指标（Population Stability Index，PSI）， 衡量未来的（测试集）样本及模型训练样本评分的分布比例是否保持一致，以评估模型的稳定性。同理，PSI也可以用衡量特征值的分布差异，评估数据特征层面的稳定性。

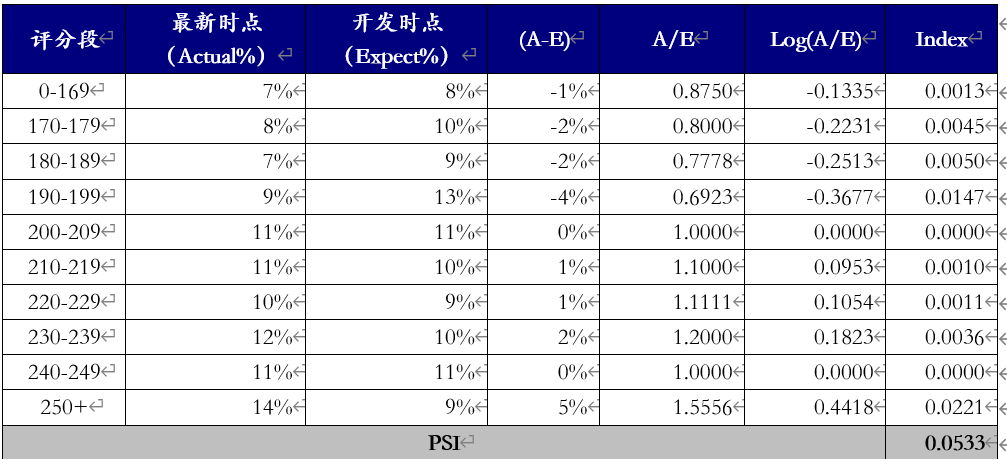
PSI计算以训练样本的模型评分作为稳定性的参考点（预期分数占比），衡量未来的实际预测分数（实际分布占比）的误差情况。计算公式为 SUM(各分数段的 (实际占比 - 预期占比）* ln(实际占比 / 预期占比) )具体的计算步骤及示例代码如下：

step1：将预期数值分布（开发数据集）进行分箱离散化，统计各个分箱里的样本占比。

step2: 按相同分箱区间，对实际分布（测试集）统计各分箱内的样本占比。

step3:计算各分箱内的A - E和Ln(A / E)，计算index = (实际占比 - 预期占比）* ln(实际占比 / 预期占比) 。

step4: 将各分箱的index进行求和，即得到最终的PSI

import math
import numpy as np
import pandas as pd

def calculate_psi(base_list, test_list, bins=20, min_sample=10):
    try:
        base_df = pd.DataFrame(base_list, columns=['score'])
        test_df = pd.DataFrame(test_list, columns=['score']) 
        
        # 1.去除缺失值后，统计两个分布的样本量
        base_notnull_cnt = len(list(base_df['score'].dropna()))
        test_notnull_cnt = len(list(test_df['score'].dropna()))

        # 空分箱
        base_null_cnt = len(base_df) - base_notnull_cnt
        test_null_cnt = len(test_df) - test_notnull_cnt
        
        # 2.最小分箱数
        q_list = []
        if type(bins) == int:
            bin_num = min(bins, int(base_notnull_cnt / min_sample))
            q_list = [x / bin_num for x in range(1, bin_num)]
            break_list = []
            for q in q_list:
                bk = base_df['score'].quantile(q)
                break_list.append(bk)
            break_list = sorted(list(set(break_list))) # 去重复后排序
            score_bin_list = [-np.inf] + break_list + [np.inf]
        else:
            score_bin_list = bins
        
        # 4.统计各分箱内的样本量
        base_cnt_list = [base_null_cnt]
        test_cnt_list = [test_null_cnt]
        bucket_list = ["MISSING"]
        for i in range(len(score_bin_list)-1):
            left  = round(score_bin_list[i+0], 4)
            right = round(score_bin_list[i+1], 4)
            bucket_list.append("(" + str(left) + ',' + str(right) + ']')
            
            base_cnt = base_df[(base_df.score > left) & (base_df.score <= right)].shape[0]
            base_cnt_list.append(base_cnt)
            
            test_cnt = test_df[(test_df.score > left) & (test_df.score <= right)].shape[0]
            test_cnt_list.append(test_cnt)
        
        # 5.汇总统计结果    
        stat_df = pd.DataFrame({"bucket": bucket_list, "base_cnt": base_cnt_list, "test_cnt": test_cnt_list})
        stat_df['base_dist'] = stat_df['base_cnt'] / len(base_df)
        stat_df['test_dist'] = stat_df['test_cnt'] / len(test_df)
        
        def sub_psi(row):
            # 6.计算PSI
            base_list = row['base_dist']
            test_dist = row['test_dist']
            # 处理某分箱内样本量为0的情况
            if base_list == 0 and test_dist == 0:
                return 0
            elif base_list == 0 and test_dist > 0:
                base_list = 1 / base_notnull_cnt   
            elif base_list > 0 and test_dist == 0:
                test_dist = 1 / test_notnull_cnt
                
            return (test_dist - base_list) * np.log(test_dist / base_list)
        
        stat_df['psi'] = stat_df.apply(lambda row: sub_psi(row), axis=1)
        stat_df = stat_df[['bucket', 'base_cnt', 'base_dist', 'test_cnt', 'test_dist', 'psi']]
        psi = stat_df['psi'].sum()
        
    except:
        print('error!!!')
        psi = np.nan 
        stat_df = None
    return psi, stat_df

## 也可直接调用toad包计算psi
# prob_dev模型在训练样本的评分，prob_test测试样本的评分
psi = toad.metrics.PSI(prob_dev,prob_test)

分析psi指标原理，经过公式变形，我们可以发现psi的含义等同于第一项实际分布（A）与预期分布（E）的KL散度 + 第二项预期分布（E）与实际分布（A）之间的KL散度之和，KL散度可以单向（非对称性指标）地描述信息熵差异，上式更为综合地描述分布的差异情况。

PSI数值越小（经验是常以<0.1作为标准），两个分布之间的差异就越小，代表越稳定。PSI值在实际应用中的优点在于其计算的便捷性，但需要注意的是，PSI的计算受分组数量及方式、群体样本量和现实业务政策等多重因素影响，尤其是对业务变动剧烈的小样本来说，PSI的值往往超出一般的经验水平，因此需要结合实际的业务和数据情况进行具体分析。