C语言算法–快速排序法
1-什么是快速排序法
快速排序(Quicksort)是一种常用的排序算法,它基于分治的思想。它的核心思想是选择一个基准元素,将数组划分为两个子数组,使得左边的子数组中的所有元素都小于等于基准元素,右边的子数组中的所有元素都大于基准元素,然后对这两个子数组递归地应用快速排序算法,直到整个数组有序。
面是快速排序的基本步骤:
- 选择一个基准元素。通常情况下,选择数组的第一个元素作为基准元素。
- 将数组划分为两个子数组,左边子数组中的元素小于等于基准元素,右边子数组中的元素大于基准元素。这个过程称为分区(Partition)。
- 对左边子数组和右边子数组递归地应用快速排序算法,直到子数组的长度为1或0,此时子数组已经有序。
- 合并子数组,得到最终的有序数组。
快速排序的关键在于分区过程。常用的分区算法是Lomuto分区和Hoare分区。Lomuto分区的实现简单但效率稍低,而Hoare分区则更高效一些。
快速排序的平均时间复杂度为O(n log n),其中n是待排序数组的长度。它是一种原地排序算法,不需要额外的存储空间,因此空间复杂度为O(1)。快速排序是一种不稳定的排序算法,意味着相等元素的相对顺序在排序后可能会改变。
动画演示(来源于网络):
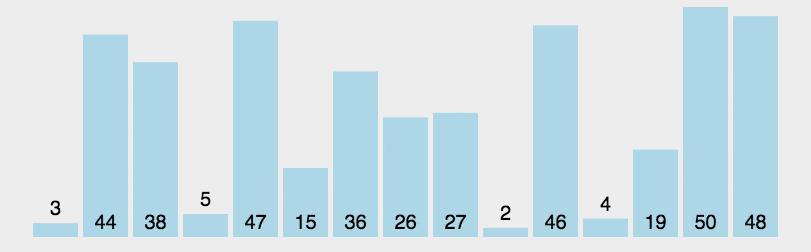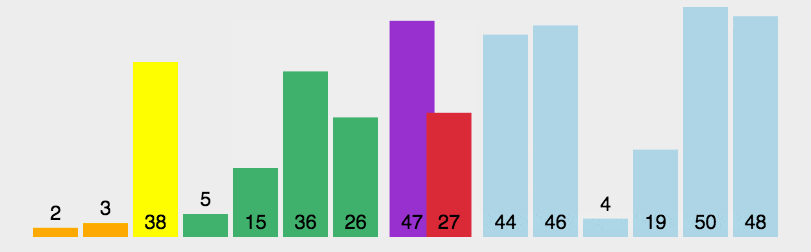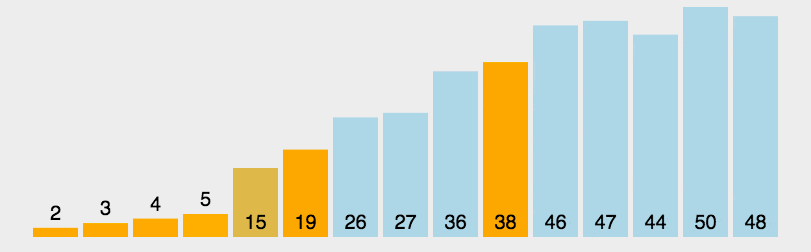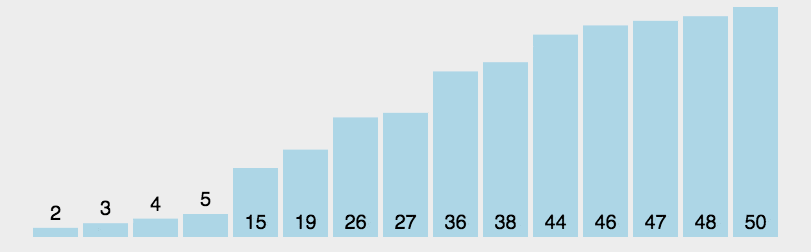
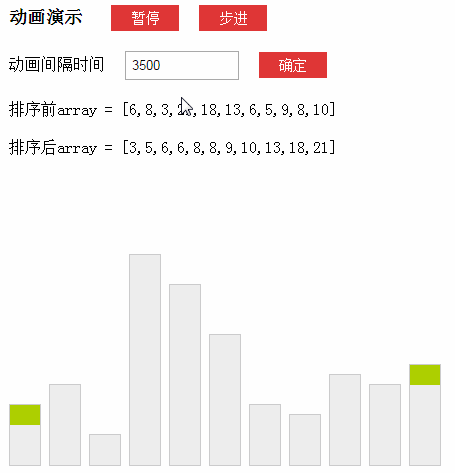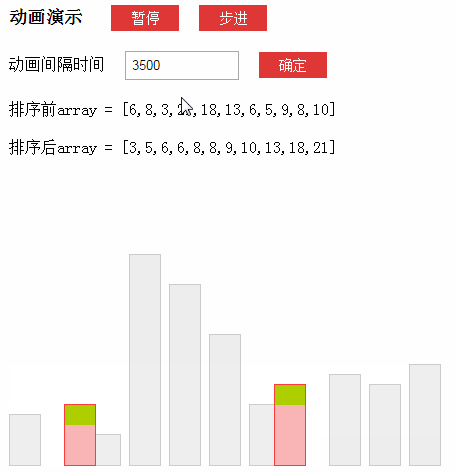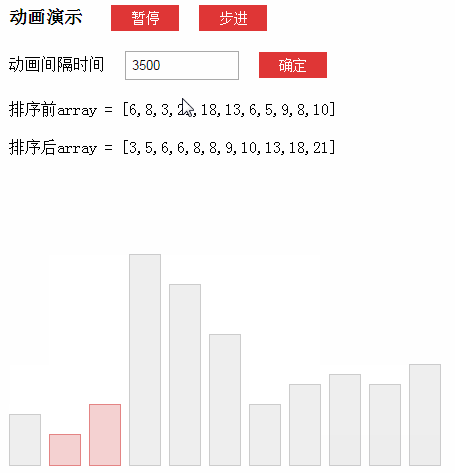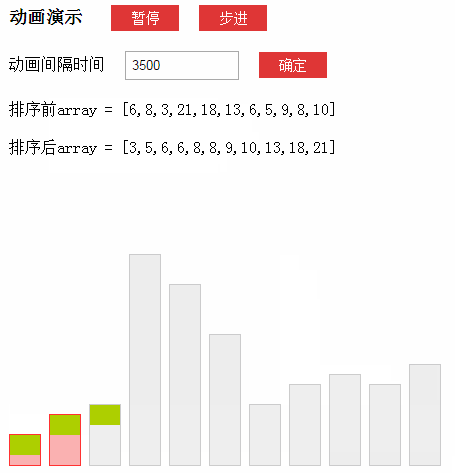
1.1-什么是Lomuto分区
Lomuto分区是一种用于快速排序算法的分区方法,由C.A.R. Hoare的经典分区方法之一。Lomuto分区算法的实现相对简单,但在某些情况下效率稍低。
下面是Lomuto分区的基本步骤:
- 选择一个基准元素。通常情况下,选择数组的最后一个元素作为基准元素。
- 遍历数组,将小于等于基准元素的元素放在数组的左边,并维护一个指针(称为分区指针),指向当前小于等于基准元素的位置。
- 遍历结束后,将基准元素放在分区指针的下一个位置,即将基准元素放在正确的位置上。
- 分区指针左边的元素都小于等于基准元素,右边的元素都大于基准元素。
- 对分区指针左边和右边的子数组递归地应用快速排序算法。
Lomuto分区的时间复杂度与快速排序相同,平均情况下为O(n log n),最坏情况下为O(n^2)(当数组已经有序或接近有序时)
1.2-什么是Hoare分区
Hoare分区是一种用于快速排序算法的分区方法,由快速排序的发明者之一、英国计算机科学家Tony Hoare在1960年提出。相对于Lomuto分区,Hoare分区在一些情况下能够更高效地进行数组的划分。
下面是Hoare分区的基本步骤:
- 选择一个基准元素。通常情况下,选择数组的第一个元素或随机选择一个元素作为基准元素。
- 定义两个指针,一个指向数组的左端,另一个指向数组的右端。
- 移动左指针,直到找到一个大于等于基准元素的元素。
- 移动右指针,直到找到一个小于等于基准元素的元素。
- 如果左指针仍然在右指针的左侧,则交换左指针和右指针所指向的元素。
- 重复步骤 3-5,直到左指针超过了右指针。
- 返回右指针作为分区点。
1.3-Hoare分区和Lomuto分区对比
Hoare分区和Lomuto分区是两种常用的分区方法,用于快速排序算法中的数组划分。它们在实现上有所不同,对比如下:
- 实现复杂度:
- Lomuto分区的实现相对简单,容易理解和实现。
- Hoare分区的实现稍微复杂一些,需要使用两个指针并处理边界情况。
- 划分方式:
- Lomuto分区从数组的最后一个元素作为基准元素开始,通过将小于等于基准元素的元素放在数组的左边,大于基准元素的元素放在数组的右边,最终将基准元素放在正确的位置上。
- Hoare分区从数组的第一个元素作为基准元素开始,通过两个指针分别从数组的两端向中间移动,交换逆序对,直到两个指针相遇,将基准元素放在分区点上。
- 效率对比:
- 平均情况下,Hoare分区相对于Lomuto分区通常更高效,因为它在划分时更均衡地将元素分配到两个子数组中。因此,Hoare分区的快速排序通常比Lomuto分区的快速排序更快。
- 然而,在某些情况下,Lomuto分区可能比Hoare分区更好。当数组中存在大量重复的元素时,Lomuto分区对于相等元素的处理更简单,可能更有效。
总的来说,Lomuto分区在实现上更简单,而Hoare分区在某些情况下更高效。在实际应用中,根据具体情况选择适合的分区方法可以提高快速排序算法的性能。另外,还有其他改进的分区方法,如三路快速排序(Dutch National Flag partitioning)等,可以进一步优化快速排序的性能。
2-快速排序法的优点
- 高效性:快速排序是一种高效的排序算法,平均情况下的时间复杂度为O(n log n)。在实际应用中,它通常比其他排序算法(如插入排序、冒泡排序等)更快速。
- 原地排序:快速排序是一种原地排序算法,不需要额外的存储空间来存储中间结果。只需要通过交换数组中的元素来进行排序,因此空间复杂度为O(1)。
- 分治思想:快速排序使用分治思想,将原问题分解为更小的子问题,通过递归地处理子问题来解决整个排序问题。这种思想使得算法的实现简单而直观。
- 可以并行化:由于快速排序的分治特性,可以将问题划分为多个子问题并独立地进行排序。这种特性使得快速排序可以很容易地并行化,利用多核处理器或分布式系统提高排序的效率。
- 适应性强:快速排序在实践中表现良好,适用于各种数据类型和规模的排序任务。它在大多数情况下都能提供高效的排序性能,并且可以通过优化的分区方法进一步提高算法的性能。
3-快速排序法的缺点
- 最坏情况下的性能:在最坏情况下,即待排序数组已经有序或接近有序的情况下,快速排序的性能会下降。此时,快速排序的时间复杂度将退化为O(n^2),其中n是待排序数组的长度。这是因为快速排序的分区点选择不当,导致每次划分只能减少一个元素的规模,而不是平均地减半。
- 不稳定性:快速排序是一种不稳定的排序算法,意味着相等元素的相对顺序在排序后可能会改变。在某些应用场景下,需要保持相等元素的相对顺序的稳定性,这时候快速排序就不适用。
- 需要额外空间:尽管快速排序是一种原地排序算法(不需要额外的存储空间),但其递归调用的栈空间会占用额外的内存。对于大规模的数据集,递归的深度可能较大,可能会导致栈溢出或者消耗过多的内存。
- 对于小规模数据效率较低:当待排序的数组规模较小时,快速排序的递归调用开销可能超过排序本身的开销。此时,其他排序算法如插入排序或者归并排序的表现可能更好。
4-快速排序法可以应用哪些场景
- 一般排序需求:快速排序是一种高效的排序算法,适用于对大规模数据集进行排序。它的平均时间复杂度为O(n log n),在实际应用中表现良好。
- 大规模数据集的排序:由于快速排序的时间复杂度较低,因此它特别适合用于对大规模数据集进行排序。快速排序的分治策略和原地排序特性使得它在处理大量数据时具有较小的内存占用。
- 数据库排序:快速排序在数据库系统中也被广泛应用于对查询结果进行排序。由于数据库查询返回的结果集可能非常大,快速排序可以快速且有效地对结果进行排序。
- 排名和统计:快速排序可以用于计算一组数据的排名或者统计特定范围内的数据。通过对数据进行快速排序,可以轻松确定某个元素的排名或者获取满足一定条件的数据。
5-举例
#include <stdio.h>
// 交换数组中两个元素的值
void swap(int* a, int* b) {
int temp = *a;
*a = *b;
*b = temp;
}
// 打印数组内容
void printArray(int arr[], int size) {
for (int i = 0; i < size; i++) {
printf("%d ", arr[i]);
}
printf("\n");
}
// 分区函数,将数组划分为左边小于基准元素,右边大于基准元素
int partition(int arr[], int low, int high) {
int pivot = arr[low]; // 选择第一个元素作为基准元素
int i = low + 1; // 左指针
int j = high; // 右指针
while (1) {
// 左指针向右移动,直到找到大于基准元素的位置
while (arr[i] < pivot && i <= high) {
i++;
}
// 右指针向左移动,直到找到小于基准元素的位置
while (arr[j] > pivot && j >= low + 1) {
j--;
}
if (i >= j) {
break;
}
// 交换左指针和右指针所指向的元素
swap(&arr[i], &arr[j]);
printArray(arr, high + 1); // 打印每一步的数组状态
}
// 将基准元素放到正确的位置上
swap(&arr[low], &arr[j]);
printArray(arr, high + 1); // 打印每一步的数组状态
return j; // 返回基准元素的位置
}
// 快速排序函数
void quickSort(int arr[], int low, int high) {
if (low < high) {
int pivot_index = partition(arr, low, high); // 获取分区点
quickSort(arr, low, pivot_index - 1); // 对左子数组递归排序
quickSort(arr, pivot_index + 1, high); // 对右子数组递归排序
}
}
int main() {
int arr[] = {10, 7, 8, 9, 1, 5};
int size = sizeof(arr) / sizeof(arr[0]);
printf("Original Array: ");
printArray(arr, size);
printf("\n");
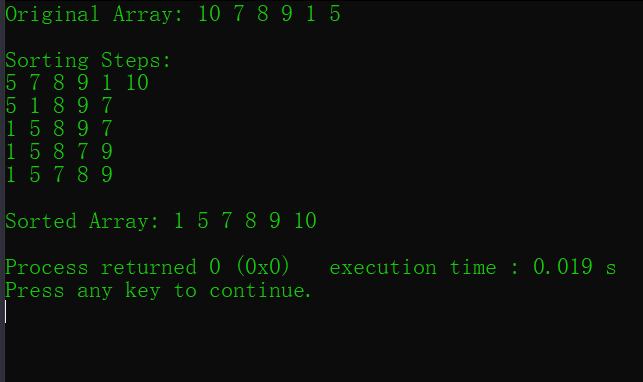
printf("Sorting Steps:\n");
quickSort(arr, 0, size - 1);
printf("\nSorted Array: ");
printArray(arr, size);
return 0;
}
#include <stdio.h>
// 枚举类型,用于表示排序步骤
enum Step
{
COMPARE,
SWAP,
PARTITION
};
// 结构体,表示数组元素
struct Element
{
int value;
enum Step step;
};
// 交换元素的值
void swap(struct Element *a, struct Element *b)
{
int temp = a->value;
a->value = b->value;
b->value = temp;
}
// 分区函数,返回分区点的索引
int partition(struct Element arr[], int low, int high)
{
int pivot = arr[high].value; // 选择最后一个元素作为基准元素
int i = (low - 1); // 分区指针,初始为低端的前一个位置
for (int j = low; j <= high - 1; j++)
{
if (arr[j].value <= pivot)
{
i++;
swap(&arr[i], &arr[j]); // 交换元素的值
}
}
swap(&arr[i + 1], &arr[high]);
return (i + 1);
}
// 快速排序函数
void quicksort(struct Element arr[], int low, int high)
{
if (low < high)
{
int pivot_index = partition(arr, low, high); // 获取分区点的索引
// 打印分区步骤
for (int i = 0; i < low; i++)
{
printf("%d ", arr[i].value);
}
printf("| ");
for (int i = low; i <= high; i++)
{
if (i == pivot_index)
{
printf("[%d] ", arr[i].value);
}
else
{
printf("%d ", arr[i].value);
}
}
printf("| ");
for (int i = high + 1; i < high; i++)
{
printf("%d ", arr[i].value);
}
printf("\n");
quicksort(arr, low, pivot_index - 1); // 递归排序左半部分
quicksort(arr, pivot_index + 1, high); // 递归排序右半部分
}
}
int main()
{
struct Element arr[] = {{7, COMPARE}, {2, COMPARE}, {5, COMPARE}, {1, COMPARE}, {8, COMPARE}, {6, COMPARE}, {3, COMPARE}, {4, COMPARE}};
int n = sizeof(arr) / sizeof(arr[0]);
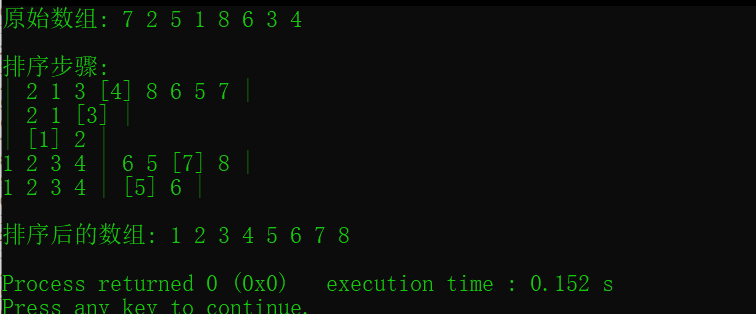
printf("原始数组: ");
for (int i = 0; i < n; i++)
{
printf("%d ", arr[i].value);
}
printf("\n\n排序步骤:\n");
quicksort(arr, 0, n - 1);
printf("\n排序后的数组: ");
for (int i = 0; i < n; i++)
{
printf("%d ", arr[i].value);
}
printf("\n");
return 0;
}