一、前言

深度学习中有许多框架，包括Tensorflow、PyTorch、Keras等，框架中实现了各种网络，并且可以自动求导，因此构建一个完整的网络只需要十几行代码。因为框架高度封装，因此我们无法知道底层的原理。为了更好地理解神经网络，本文使用numpy构建一个完整的神经网络，并实现反向传播和梯度下降算法，使用自己实现的神经网络训练一个分类模型。

二、感知机

在开始构建神经网络之前，需要了解一下神经网络的一些理论。本文要实现的是全连接神经网络，而全连接神经网络则是由一个叫感知机的模型演变而来的，下面我们来看看感知机。

2.1 感知机

2.1.1 感知机原理

感知机是一个二分类模型，其目的就是使用一个直线或超平面将两类数据分开。为了简单，这里讨论二维的情况。二维空间中的直线可以用下面的函数来表示：
$h = w_1x_1+w_2x_2+b$
其中 $x_1、x_2$ 为数据， $w_1、w_2、b$ 为参数，是三个常数。此时可以用 $X=[x_1, x_2]^T$ 来表示输入。如果输入一个 $X_1$ ，得到的 $h_1$ 大于0，说明数据 $X_1$ 在直线上方，即 $X_1$ 属于类别1。如果得到 $h_1$ 小于0，说明数据 $X_1$ 在直线下方，即 $X_1$ 数据类别0。
上面的文字描述可以用一个阶跃函数来代替，即：
$\begin{cases} 1, & w_1x_1+w_2x_2+b \geq 0\\ 0,& w_1x_1+w_2x_2+b < 0 \\ \end{cases}$
现在只需要确定 $w_1、w_2、b$ ，就可以用上述函数进行分类了。

2.1.2 逻辑电路

现在知道了感知机的函数，接下来可以用感知机来实现一些功能了。比如与电路，与电路有两个输入，分别对应 $x_1、x_2$ ，有一个输出对应y。与电路的特点是当两个输入都为1时才输出1，否则输出0，与电路的真值表如下所示：

x1	x2	y
0	0	0
0	1	0
1	0	0
1	1	1
通过一些手段，我们知道当 $w_1=0.5、w_2=0.5、b=0.8$ 时，感知机可以实现与电路的功能。现在，只需要修改 $w_1、w_2、b$ 的取值，我们还可以实现或、与非电路。下面是与电路的一个Python代码：

import numpy as np

def AND(X):
    # w1、w2
    W = np.array([[0.5], [0.5])
    b = 0.8
    h = np.dot(X, W)
    if h >= b:
        return 1
    else:
        return 0

而或、非电路的实现就是把W、b修改一下。

2.2 感知机的局限

在前面我们用感知机实现了与电路，或、与非电路也可以和与电路一样简单实现。那么感知机什么电路都能实现吗？答案是否定的，感知机是一个线性模型（用直线划分），它只能解决线性可分的问题，而异或电路则是非线性的，异或当输入相同时输出0，输入不同输出1。因此异或的输入和输出的关系可以用下图表示：
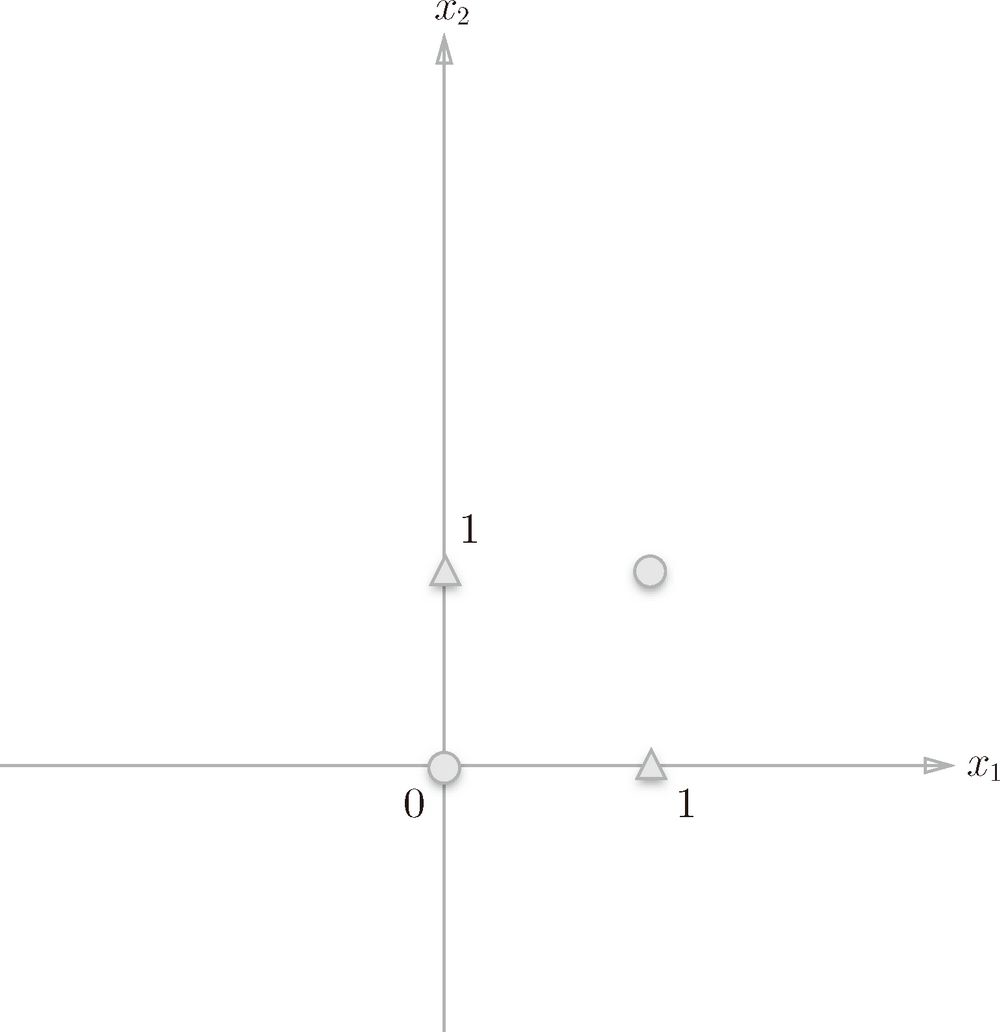
在这里插入图片描述
其中圆表示类别0，三角表示类别1。而感知机要做的是用一条直线把两类数据分开，实际上这是做不到的。
虽然用一条直线无法将两类数据分开，但是如果能用两条直线的话，就可以将两类点分开，从而就引出了多层感知机的概念。

2.3 多层感知机

虽然现在的计算机相当复杂，但是本质上还是有与、或、与非电路实现的。通过各种电路的拼接，实现复杂的计算机。按照这一思路，我们可以将多个感知机进行拼接，得到一个更复杂的电路。现在假如我们已经实现了与门（AND）、或门（OR）、与非门（NAND），这三个门用下面三个图来表示：
在这里插入图片描述
那么应该怎么组合从而实现异或门呢？

各个门的特点如下：
与门：输入都为1，输出1，否则输出0
或门：输入一个为1，输出1，否则输出0
与非门：与与门相反

我们可以按照如下所示来拼接感知机（电路），从而实现异或门：
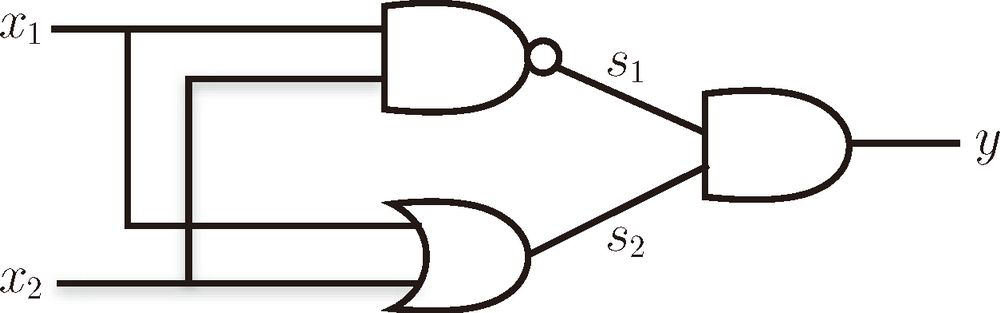
在这里插入图片描述
下面用真值表来验证一下，将 $x_1、x_2$ 代入上面的多层感知机可以得到下表结果：

x1	x2	s1	s2	y
0	0	0	1	0
0	1	1	1	1
1	0	1	1	1
1	1	0	1	0

而异或门用代码实现也非常简单，具体代码如下：

def XOR(x1, x2):
    s1 = NAND(x1, x2)
    s2 = OR(x1, x2)
    return AND(s1, s2)

三、神经网络

现在我们对多层感知机有了一些了解，那么神经网络和多层感知机有什么联系呢？这里就要关注一下前面的阶跃函数了。

3.1 激活函数

在前面感知机的输出会经过阶跃函数，将任意的值映射为0-1。但是阶跃函数不方便求导，因此就想到用一个连续函数来替代阶跃函数，其中比较常用的一个就是sigmoid函数，其函数如下：
$\sigma(x) = \frac{1}{1+e^{-x}}$
其函数图像如下：
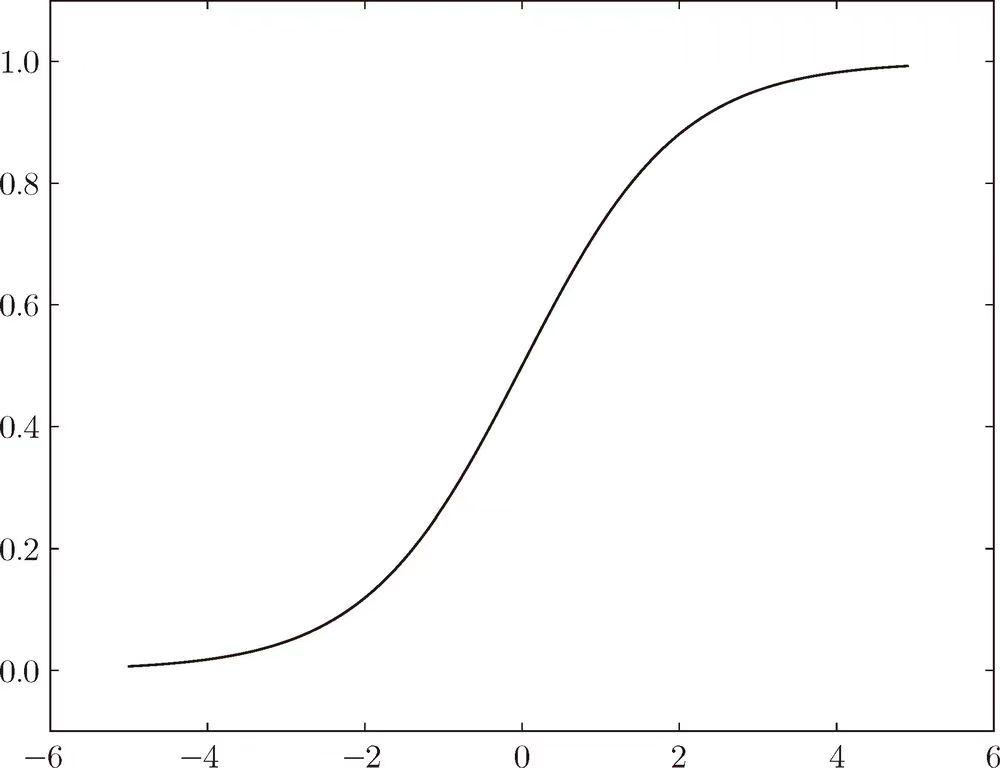
在这里插入图片描述
图像处处可导。sigmoid在神经网络发展早期非常受欢迎，但是现在在大多数场景中都被ReLU函数取代。ReLU函数更简单，求导的复杂度也更低，而且能缓解梯度消失的问题，因此更常用。ReLU的表达式如下：
$re l u (x) = ma x (x, 0)$
当输入小于0时，则返回0，当输入大于0时则返回原值。其函数图像如下：
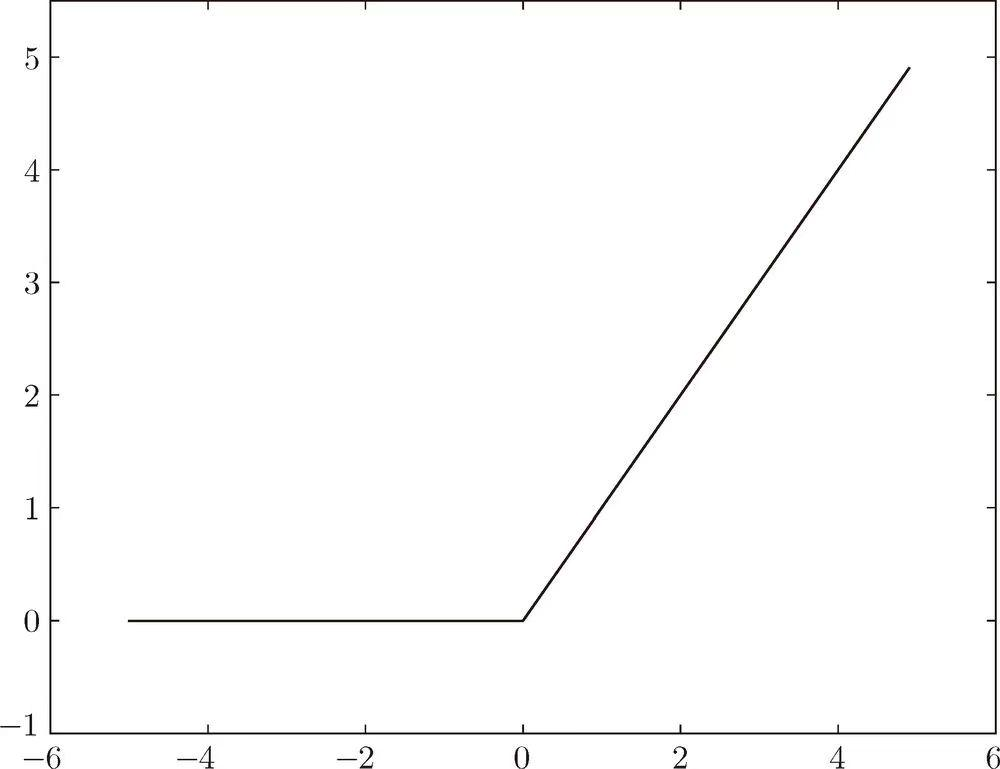
在这里插入图片描述
像前面提到的阶跃函数、sigmoid函数、ReLU函数都叫激活函数。

3.2 从多层感知机到神经网络

现在把感知机的激活函数从阶跃函数修改为ReLU函数，这样就完成了多层感知机到神经网络的蜕变。下面我们从另一个角度来理解多层感知机。这里以异或门为例，异或门中有三个逻辑门电路，不管是与门、或门还是与非门，其实都是同一个函数换了不同的参数。因此可以把异或门用下面的图表示：
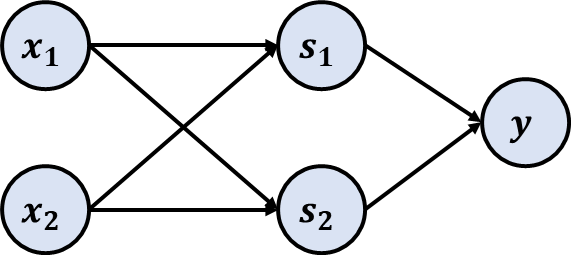
在这里插入图片描述
我们把输入用向量 $X=[x_1, x_2]^T$ 表示，而中间的输出用 $S=[s_1, s_2]^T$ ，权重用 $W=[w_1, w_2]$ 表示。那么 $s_1 = WX+b、s_2 = Wx+b$ 。但是需要注意，s1原本是与非门的结果，而s2是或门的结果，因此s1对应的W与s2对应的W是不同的。由此得到 $s_1 = W_1X+b、s_2 = W_2x+b$ ，其中 $W_1=[w_{11}, w_{12}]、W_2=[w_{21}, w_{22}]$ 。
进一步把向量 $W_1、W_2$ 组成一个矩阵，得到 $W^{(1)}=\begin{pmatrix} w_{11} & w_{12}\\ w_{21} & w_{22} \end{pmatrix}$
那么：
$S=W^{(1)}X+b$
这样就用一个矩阵乘法表示出了S的计算，同样y的计算也可以用一个矩阵乘法计算：
$y=W^{(2)}S+b$
但是上面的表达式其实没有激活函数，如果加入激活函数则可以用下面的表达式计算：
$\sigma(W^{(2)}relu(W^{(1)}X+b)+b)$
而上面的表达式就是神经网络了。