1.统计子矩阵

思路:二维前缀和超时,下面是前缀和加双指针,对列前缀和,两个玄幻控制行号,双指针控制列的移动
考查:前缀和+双指针
import os
import sys
# 请在此输入您的代码
# 矩阵大小 N × M
n,m,k=map(int,input().split()) #默认用空格隔开
s=[[0 for i in range(m+1)]] #定义一个数组
for i in range(1,n+1):
s.append([0]+list(map(int,input().split())))
for j in range(1,m+1):
s[i][j]+=s[i-1][j] # 列的前缀和
res=0
for i in range(1,n+1):
for j in range(i,n+1): #枚举上下边界
l=1 #双指针,对列用的双指针
sum=0
for r in range(1,m+1): #这部分计算的是区域和
sum+=s[j][r]-s[i-1][r] #r列的值+
while sum>k:
sum-=s[j][l]-s[i-1][l]
l+=1
res+=r-l+1
print(res)附上二维前缀和代码
import os
import sys
# 请在此输入您的代码
n,m,k = map(int,input().split())
a=[[0] for i in range(n)]
a.insert(0,[0]*(m+1))
for i in range(1,n+1): # 转换二维矩阵形式,即下标从1开始
a[i].extend(map(int,input().split()))
s = [[0]*(m+1) for i in range(n+1)] # 预计算前缀和s[][]
for i in range(1,n+1):
for j in range(1,m+1):
s[i][j] = s[i-1][j]+s[i][j-1]-s[i-1][j-1]+a[i][j]
ans =0
for i1 in range(1,n+1):
for i2 in range(i1,n+1):
for j1 in range(1,m+1):
for j2 in range(j1,m+1):
cal = s[i2][j2]-s[i2][j1-1]-s[i1-1][j2]+s[i1-1][j1-1]
if cal<= k: ans+=1
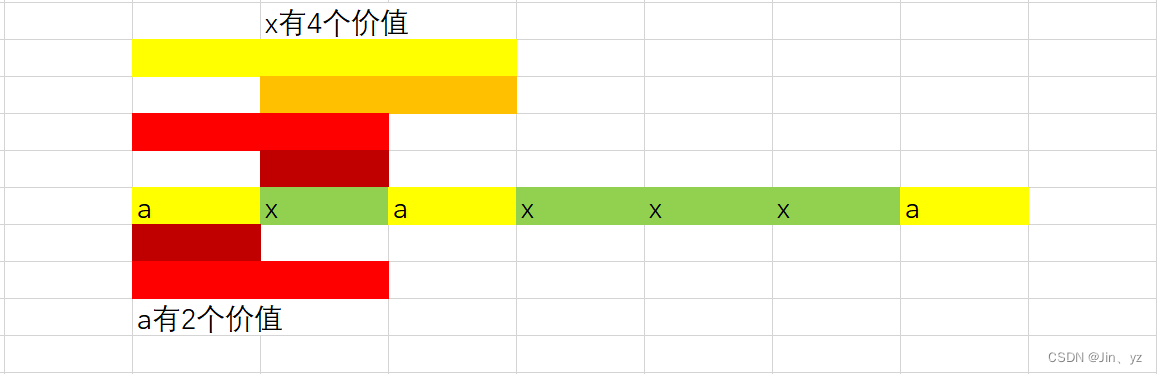
print(ans)2.子串分值

把问题转换为单个字符能够创造的的价值求和,就是他当前x下标与前后x下标内下标的组合
考查:思维
s = ' ' + input()
n = len(s) - 1
index = {}
# 计算每一个元素能创造的价值
# 累计每一个元素的价值
for i in range(1, n + 1):
c = s[i]
if c not in index:
index[c] = [0]
index[c].append(i) #记录出现的位置
cnt = 0
for value in index.values():
value.append(n + 1)
# size = len(value)-2
for i in range(1, len(value) - 1):
cnt += (value[i] - value[i - 1]) * (value[i + 1] - value[i]) # 有多少取的种方法,就是它能创造的组合
print(cnt)3.蓝桥杯国赛题目机器人塔
DFS搜索或者循环来做,可以学习Python缓存lru_cache的用法,即内置记忆化存储,用了这个可以加快运算效率,避免重复运算。
这道题结合二进制,同时从下到上递推,然后用了位运算等知识。

'''
# python3.6
# -*- coding: utf-8 -*-
# @Time : 2023/5/12 13:01
# @Author : Jin
# @File : test2.py
# @Software: PyCharm
import os
import sys
import math
# 请在此输入您的代码
#机器人塔
from functools import lru_cache
a,b=(int(i) for i in input().split())
n=int(math.sqrt((a+b)*2))
@lru_cache(None)
def f(n,x,a,b):
if n==1: # 出去边界
if x==0:
return a-1==0
else:
return b-1==0
if a<0 or b<0 : # 直接剪枝
return
#print(bin(x))
cnt=bin(x)[2:].count('1')
a=a-(n-cnt)
b=b-cnt
next=(x^(x>>1))&((2**(n-1)-1))
#print(bin(next))
return f(n-1,next,a,b)
c=0
for m in range(0,1<<n):
if f(n,m,a,b): # 层数,状态,机器人数量a 0,机器人数量b 1
c+=1
print(c)
'''
import os
import sys
# A-AA/BB; B-AB/BA,A-0; B-1;符合异或运算
m, n = map(int, input().split())
def check(now, num):
num_a, num_b = 0, 0
for i in range(num, 1, -1): # i是层数也是机器人个数
ls = list(bin(now))[2:]
num_b += ls.count('1')
num_a += i - ls.count('1')
# 求上一层的状态
# now右移一位相当于把now最低位的状态移走,再和原本的now异就得到上层结果,但是最高位要通过与运算去掉,
# 这相当于原本的now除了最高位其他每一位都和前一位进行了异或,结果为1说明可以站B,为0站A
now ^= (now >> 1)
now &= (2**(i - 1) - 1) # 移除now最高位的状态
if now == 1: num_b += 1
else: num_a += 1
return num_a == m and num_b == n
# num*(num+1)//2 = m+n
num = int(((m + n) * 2) ** 0.5) # 层数0~num-1 ,最后一层的个数
ans = 0
for i in range(1 << num): # 最下面一层有num个数,有00..~11..种状态
if check(i, num): ans += 1
print(ans)4.跳蚂蚱
BFS模板题,主要是这个可以使用双向广搜,BFS双向广搜,了解一下写法。注意有时候BFS需要结合copy库来使用

import collections
import sys
meet=False #判断是否相遇
def extend(q,m1,m2):
global meet
s=q.popleft()
ss=list(s)
index=ss.index('0') #找0的索引
for j in [1,-1,2,-2]:
ss[(index+j+9)%9],ss[index]= ss[index],ss[(index+j+9)%9]
a=''.join(ss)
if a in m2: # 找到相同的了,即相遇了
print(m1[s]+1+m2[a])
meet=True
return
if a not in m1:
q.append(a)
m1[a]=m1[s]+1 # 向字典中添加
ss[(index+j+9)%9],ss[index]= ss[index],ss[(index+j+9)%9]
# meet=False
q1=collections.deque()
q2=collections.deque()
q1.append("012345678")
q2.append("087654321")
# 字典去重,同时记录步数
mp1={'012345678':0} ; mp2={'087654321':0}
while q1 and q2 : # 两个都不为空
if len(q1)<=len(q2): extend(q1,mp1,mp2)
else: extend(q2,mp2,mp1)
if meet==True: break
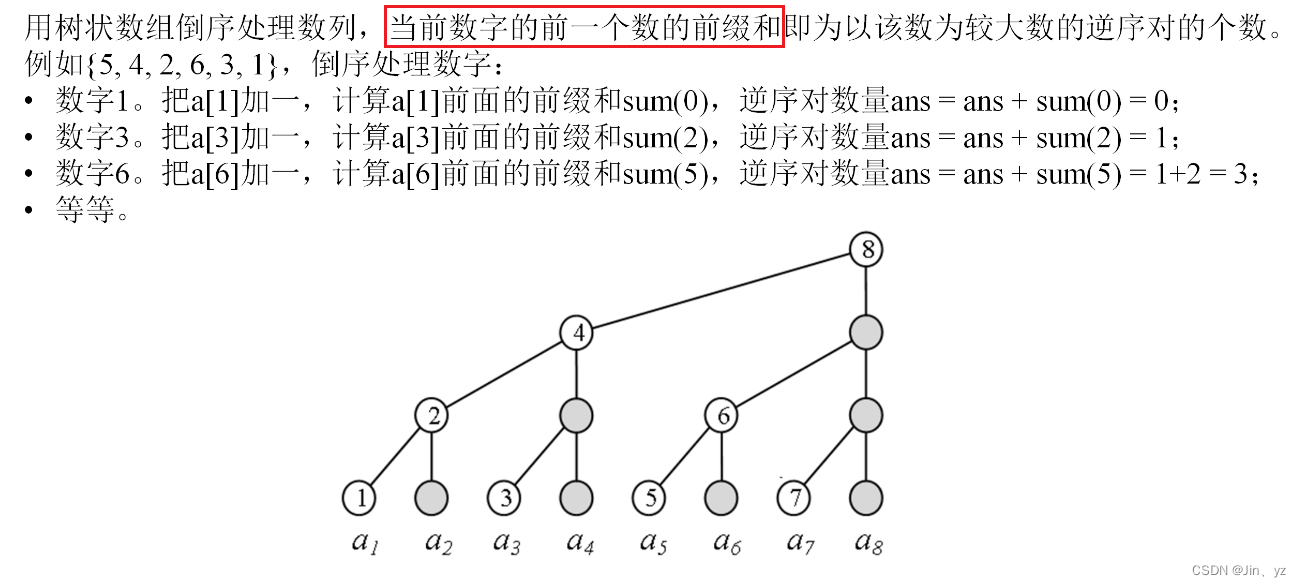
5.树状数组处理逆序对
逆序对,两种方法,前面比他大的(正序树状数组),后面比他小的(倒叙树状数组),


import os
import sys
# 每个人的交换次数等前面严格大于自身的人数+后面严格小于自身的人数 数据范围是10^5暴力枚举O(n^2)会超时,此时就想到要用的树状数组或归并排序
#只有60%
# 请在此输入您的代码
N=1000010
def discretization(h):#数组离散化
temp=list(set(h))
temp.sort()
for i in range(len(h)):
h[i]=temp.index(h[i])+1
def lowbit(x):
return x&-x
def update(x,d):
while x<=N:
tree[x]+=d
x+=lowbit(x)
def sum(x):
ans=0
while x>0:
ans+=tree[x]
x-=lowbit(x)
return ans
n=int(input())
hold=list(map(int,input().split())) #身高
h=[0 for i in range(N)]
for i in range(n): # 转为下标从1开始
h[i+1]=hold[i]
discretization(h) #数组离散化,但是因为本题的数字没超出范围就不需要了
k=[0 for i in range(N)]#每个小朋友要交换的次数
tree=[0 for i in range(N)] # 树状数组
for i in range(1,n+1): #正序处理,他后面的逆序对数量
update(h[i],1)
k[i]=i-sum(h[i]) # 计算h[i]前面的逆序数,前面有i-sum(h[i])个比他大的
tree=[0 for i in range(N)]
for i in range(n,0,-1): #倒序处理,他前面的逆序对数量
k[i]+=sum(h[i]-1) #计算h[i],后面有sum(h[i]-1)个比他小的
update(h[i],1)
res=0
for i in range(1,n+1):
res+=int((1+k[i])*k[i]/2) #等差数列
print(res)归并排序处理逆序对
def merge_sort(L,R):
if L < R:
mid = (L+R)//2
merge_sort(L,mid)
merge_sort(mid+1,R)
merge(L,mid,R)
def merge(L,mid,R):
global res # 记录答案
i=L;j=mid+1;t=0
while(i<=mid and j<=R): #归并
a[i]
a[j]
if (a[i]>a[j]): #4 5 / 2 3 L=0 mid=1,R=3
b[t]=a[j];t+=1;j+=1;
res = res+(mid-i+1) # 记录逆序对数量
else:
b[t] = a[i];t += 1;i += 1
# 其中一个处理完了,把剩下的复制过来,直接整体复制
# 这里注意区间取值,采用的是整体复制的思想,b是辅助数组
if i<=mid: b[t:R-L+1]=a[i:mid+1] # 取不到mid+1
elif j<=R:b[t:R-L+1]=a[j:]
# 把排序好的b[]复制回去a[]
a[L:R+1]=b[:R-L+1]
n= int(input())
a = list(map(int,input().split()))
b = [0]*n
res = 0
merge_sort(0,n-1)
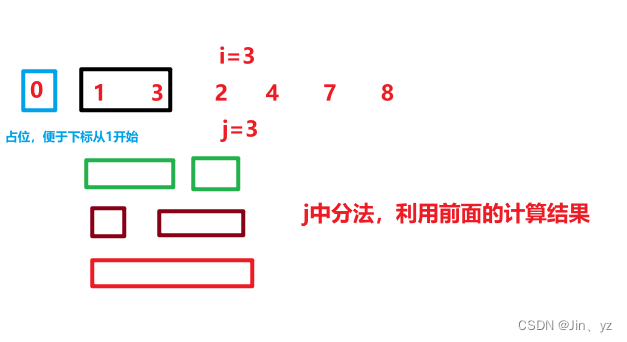
print(res)6.数组切分

DP的做法,python效率低所以不能AC
# 超时了两个,80%,思路没问题
mod = 1000000007
N = 10010
f = [0 for i in range(N)]
n = int(input())
a =[0]+ list(map(int,input().split()))
f[0]=1
for i in range(1,n+1):
mx=a[i]
mi=a[i]
for j in range(i,0,-1):
mx = max(mx,a[j])
mi = min(mi,a[j])
if mx-mi == i-j:
f[i] = (f[i]+f[j-1]) % mod #dp思想 一个指针依次遍历i,另一个从当前位置回滚回去,长度从1变大,利用前一步结果计算
print(f[n])






![[数据结构 -- C语言] 队列(Queue)](https://img-blog.csdnimg.cn/img_convert/6dbb63a1b5f184a2f1f5413eba102d33.png)