​# 1. 论文信息

论文名称	Deep Supervised Dual Cycle Adversarial Network for Cross-Modal Retrieval
作者	Lei Liao 中山大学
会议/出版社	IEEE Transactions on Circuits and Systems for Video Technology
pdf	📄在线pdf
代码	💻无代码

本文是基于公共空间的跨模态检索方法。文章中提出了 DSDCAN 的方法，由两个 Cycle GAN 组成，该方法通过原始特征生成模态样式特征和公共空间特征。通过交换模态样式特征进行重建缩小了两个模态之间的差异。将标签文本嵌入到公共空间中，通过对抗训练和语义区分度损失优化公共空间的表示，并且通过二阶度量函数来弥补分布之间的差异。同时还使用了标签进行分类。

这篇文章中使用了多个对抗性训练，并且集成了一些弥补模态差异的 loss。模型的结构和一些公共特征解耦的模型比较像。看实现效果 MAP 得分很高。

2. introduction

之前的方法的不足之处在于它们在公共空间中将模态样式和语义内容混合在一起，而没有充分探索语义内容的语义和区分性表示/重建。这通常会导致检索性能不佳。

为了解决这些问题，作者提出了一种新的深度监督双循环对抗网络（DSDCAN）模型，它能够解开语义内容和模态样式特征，并通过充分利用语义和标签监督来增强公共空间表示的语义区分性。此外，它还引入了二阶相似性来测量公共空间中跨模态表示的距离。这些特点使得该方法能够更好地保留语义信息并增强特征的区分性。

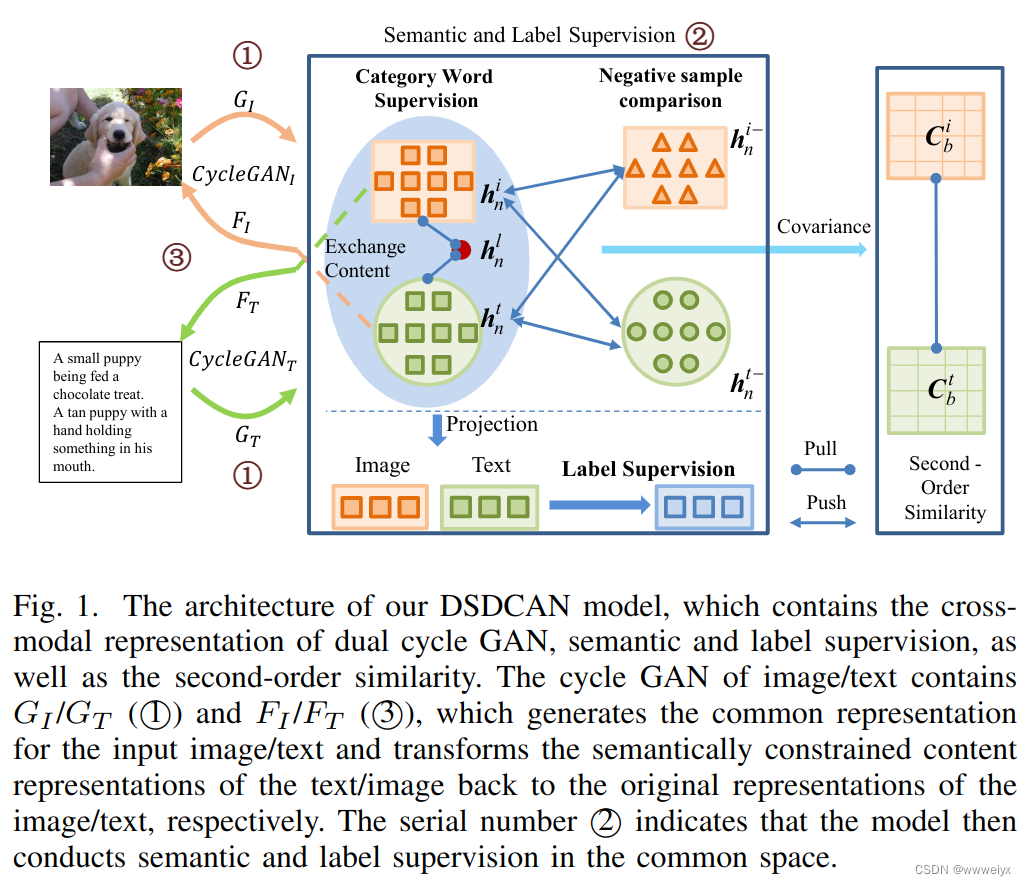
本文的主要贡献可以概括为：

1. 提出了 cross-modal dual cycle GAN network framework，将特征解耦成语义内容和模态分割部分，通过交换不同模态的语义内容并利用模态样式进行跨模态重建。
2. 为了更好地进行有监督的训练，将类别嵌入构建判别语义损失和标签损失。类别嵌入在训练过程中动态更新，以更好地进行分类。
3. 设计了一种新的跨模态相似性损失，通过二阶相似性来测量公共空间中跨模态表示的距离。

相关工作：1. 基于深度神经网络的方法。2. 基于生成对抗网络（GAN）的方法。3. 跨模态哈希方法。

3. method

The DSDCAN Framework

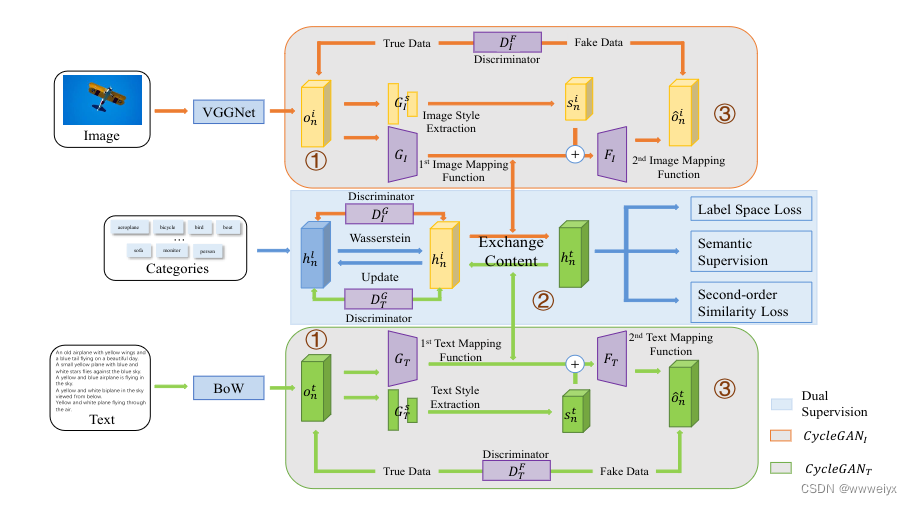
整个框架包括了 8 个模型，分别是用于学习公共空间特征的 $G_I$ 和 $G_T$；用于学习模态样式特征的 $G_I^S$ 和 $G_T^S$；用于重建特征的 $F_I$ 和 $F_T$；用于判别公共空间特征和标签语义特征的 $D_I^G$ 和 $D_T^G$；用于判别原始特征和重建特征的 $D_I^F$ 和 $D_T^F$。8 个模型交替优化。除了使用图像特征和文本特征之外，本文还将标签文本作为信息嵌入到了公共空间中优化训练效果。

按照功能可能分为以下几类：

1. 生成公共空间特征部分：

   $o_n^i$ 和 $o_n^t$ 分别为图像和文本的原始特征。分别通过图像 CycleGAN $G_I$ 和文本 CycleGAN $G_T$ 的第一个映射函数提取公共空间内容表示 $h_n^i$ 和 $h_n^t$ 特征。$G_I:{\mathbf{o}}_n^i\to {\mathbf{h}}_n^i$，$G_T:{\mathbf{o}}_n^t\to {\mathbf{h}}_n^t$。$D_I^G$ 和 $D_T^G$ 分别是图像分支和文本分支的判别器。判别器将类别语义特征和公共空间特征分别视为真数据和假数据。.

2. 模态风格特征生成部分：

   使用了两个全连接层从原始特征中提取模态样式特征，其中包括图片：${\mathbf{s}}_n^i=G_I^s\left({\mathbf{o}}_n^i\right)$ 和文本：${\mathbf{s}}_n^t=G_T^s\left({\mathbf{o}}_n^t\right)$ 公共空间内容表示和模态样式特征通过图像 CycleGAN $G_I$ 和文本 CycleGAN $G_T$ 的第二个映射函数重建出另一个模态的原始特征。

3. 模态重建特征生成部分：

   交换不同的语义内容特征进行重建，生成重建后的原始特征 ${\hat{\mathbf{o}}}_n^t=F_I\left({\mathbf{h}}_n^2+{\mathbf{s}}_t\right)$ 和 ${\hat{\mathbf{o}}}_n^i=F_T\left({\mathbf{h}}_n^t+{\mathbf{s}}_i\right)$ 。为了减少图像和文本之间的媒体鸿沟，判别器 $D_I^F$ 和 $D_T^F$ 将原始的特征视为真实数据，重建后的特征视为伪造数据，通过对抗训练增加之间的相似度（判别器无法区分特征是否是原始还是重建的，说明重建后的差异较小）。并且使用 Wasserstein distance 去最大化重建特征和原始特征的相似度。

训练损失

在公共空间中，本文提出了一种语义判别和标签损失来增强特征区分度。对于同类不同模态的数据提出了基于二阶度量的相似度损失。跨模态重建损失和设计损失不仅能缩小模态间的差距还可以使用特征更具判别性。

跨模态重建损失

跨模态重建损失的作用是最小化原始特征和重建特征之间的差异，来保证公共空间特征的跨模态相关性。

1. 跨模态重建损失定义为：

   $L_F=E_{i\sim {\mathcal{P}}_i}\left[L_{F_I}\right]+E_{t\sim {\mathcal{P}}_t}\left[L_{F_T}\right]$

   • 其中， $L_{F_I}=W\left(\mathrm{con}\left(D_I^F\left({\hat{\mathbf{o}}}_n^i\right)\right),\mathrm{con}\left(D_I^F\left({\mathbf{o}}_n^i\right)\right)\right)$ 和 $L_{F_T}=W\left(\mathrm{con}\left(D_T^F\left({\hat{\mathbf{o}}}_n^t\right)\right),\mathrm{con}\left(D_T^F\left({\mathbf{o}}_n^t\right)\right)\right)$.

   • W() 代表了 Wasserstein distance

   • $\mathrm{con}(\ast )$ means to concatenate the input, the output of the hidden layer, and the final output

2. 判别器损失定义为：

   $L_D^F=E_{i\sim {\mathcal{P}}_i}\left[L_{D_I}^F\right]+E_{t\sim {\mathcal{P}}_t}\left[L_{D_T}^F\right]$

   where $L_{D_I}^F=\log \left(D_I^F\left({\mathbf{o}}_n^i\right)\right)+\log \left(1-D_I^F\left({\hat{\mathbf{o}}}_n^i\right)\right)$ and $L_{D_T}^F=$ $\log \left(D_T^F\left({\mathbf{o}}_n^t\right)\right)+\log \left(1-D_T^F\left({\hat{\mathbf{o}}}_n^t\right)\right)$

进行对抗性训练

语义区分度和标签损失

目的：通过语义标签特征和标签指导 $G_I$ 和 $G_T$ 去生成更有语义区分度的公共空间特征。

1. 语义有监督损失

   公式定义为：$L_{Sem}=L_{G_I}+L_{G_T}+L_{NI}+L_{NT}$

   前两项的最小化生成的公共空间特征和类别词汇特征之间的距离，后两项构建三元组损失优化特征空间

   $\begin{array}{rl}{L}_{G_I}& =W\left(\mathrm{con}\left(D_I^G\left({\mathbf{h}}_n^i\right)\right),\mathrm{con}\left(D_I^G\left({\mathbf{h}}_n^l\right)\right)\right)\\ L_{G_T}& =W\left(\mathrm{con}\left(D_T^G\left({\mathbf{h}}_n^t\right)\right),\mathrm{con}\left(D_T^G\left({\mathbf{h}}_n^l\right)\right)\right)\end{array}$​$\begin{array}{rl}{L}_{NI}& ={\left[\tau {\Vert {\mathbf{h}}_n^i-{\mathbf{h}}_n^l\Vert }_2-{\Vert {\mathbf{h}}_n^i-{\mathbf{h}}_n^{i-}\Vert }_2-{\Vert {\mathbf{h}}_n^i-{\mathbf{h}}_n^{t-}\Vert }_2\right]}_{+}\\ L_{NT}& ={\left[\tau {\Vert {\mathbf{h}}_n^t-{\mathbf{h}}_n^l\Vert }_2-{\Vert {\mathbf{h}}_n^t-{\mathbf{h}}_n^{t-}\Vert }_2-{\Vert {\mathbf{h}}_n^t-{\mathbf{h}}_n^{i-}\Vert }_2\right]}_{+}\end{array}$

   类别词的嵌入作为每类的中心，在训练过程中不断更新。

2. 标签空间损失

   使用正交矩阵 $P$ 作为线性分类器，标签损失定义为：

   $L_{Lab}={\Vert {\mathbf{P}}^T{\mathbf{h}}_n^i-{\mathbf{y}}_n\Vert }_2+{\Vert {\mathbf{P}}^T{\mathbf{h}}_n^t-{\mathbf{y}}_n\Vert }_2$

二阶相似度损失

为了进一步保留模态特征类别区分能力，作者还使用了二阶相似度损失。

$L_{CM}={\Vert {\mathbf{H}}_b^i-{\mathbf{H}}_b^t\Vert }_2+{\Vert {\mathbf{C}}_b^i-{\mathbf{C}}_b^t\Vert }_2$

使用协方差矩阵来衡量模态之间的相似性。公式的第一部分直接最小化了共同表示中的跨模态距离，可以保证不同模态之间在共同表示中具有相似的表示。第二部分通过最小化图像和文本表示之间的协方差矩阵的差异，使得不同模态之间的数据分布结构更加相似，可以帮助保留跨模态任务中的分类信息。

DSDCAN 总损失函数

DSDCAN 被分为三个交替优化的部分：

1. 第一部分：对于特征嵌入部分生成器 $G_I$ 、 $G_T$ 和判别器 $D_I^G$ 、 $D_T^G$ 的优化，优化的损失定义为：

   $\begin{array}{rl}{L}_{D_I}^G& =\log \left(D_I^G\left({\mathbf{h}}_n^l\right)\right)+\log \left(1-D_I^G\left({\mathbf{h}}_n^i\right)\right)\\ L_{D_T}^G& =\log \left(D_T^G\left({\mathbf{h}}_n^l\right)\right)+\log \left(1-D_T^G\left({\mathbf{h}}_n^t\right)\right)\end{array}$

   用于判断公共空间中的特征是来自 category word embedding 还是来自生成器生成

2. 第二部分：对重建部分生成器$F_I$ 、 $F_T$ 和判别器 $D_I^F$ 、 $D_T^F$ 的优化，优化损失的定义为：

   $L_D^F=E_{i\sim {\mathcal{P}}_i}\left[L_{D_I}^F\right]+E_{t\sim {\mathcal{P}}_t}\left[L_{D_T}^F\right]$

3. 第三部分：整个 dual cycle GAN 的损失，定义为：

   $L_G=L_{Sem}+L_{Lab}+L_{CM}+\lambda L_F$

   其中，$L_{Sem}$ 为语义区分度损失，$L_{Lab}$ 为标签损失，$L_{CM}$ 为二阶相似性损失，$L_F$ 为重建损失

4. experiments

4.1 数据集以及评价指标

数据集：

评价指标：MAP

4.2 实验

1. Comparative Experiment：作者进行了比较实验来验证DSDCAN模型的有效性。作者将DSDCAN模型与传统方法（CCA、JRL）和当前最先进的基于深度学习的方法（DCCA、MMSAE、DSCMR、SDML、DRSL、AGCN）以及基于对抗学习的方法（ACMR、AACR、DADN和MS2GAN）进行了比较。实验结果表明，DSDCAN模型在所有数据集上都取得了最佳性能，并且优于其他方法。
2. Ablation Study：行了消融实验来验证DSDCAN模型中每个部分的有效性，结果表明，所有这些部分都对模型的性能有所贡献。实验结果表明，DSDCAN模型在所有实验中都取得了最佳性能，并且优于其他现有方法和传统方法。
3. Parameter Analysis：作者进行了参数分析来研究DSDCAN模型中的不同参数对模型性能的影响。作者主要研究了更新分类词嵌入的速率β对模型性能的影响。作者通过实验发现，当β取值较小时，模型性能较差；当β取值较大时，模型性能也会下降。作者建议将β设置为0.01以获得最佳性能。
4. Efficiency Analyses：作者进行了效率分析来研究DSDCAN模型的计算效率。作者主要比较了DSDCAN模型和其他几种跨模态检索方法的计算时间和内存占用情况。实验结果表明，DSDCAN模型具有较高的计算效率，并且可以处理大规模数据集。

5. 代码

无

‍