AVL树
文章目录
- 前言
- 一、AVL树的实现
- 总结
前言
一、AVL树的实现
首先我们直接实现KV结构的AVL树，因为如果KV结构的树都会了那么在写K的就很简单了，只需要在KV结构上修改一些值即可。
要注意：AVL数相比原先的二叉搜索树多了一个平衡因子，只有平衡因子的绝对值不超过1或者小于-1才是AVL树，如下图所示：
这里默认是新增节点在右树平衡因子就+1，新增节点在左树平衡因子就-1，这里为什么让AVL树的高度差不超过1呢，因为没有办法让一颗二叉搜索树完全平衡。注意：AVL树不一定有平衡因子，使用平衡因子只是一种实现方式。
下面我们先创建树的节点：
为了避免冲突，我们将我们写的树放在命名空间中：
template<class K,class V>
struct AVLTreeNode
{
AVLTreeNode<K, V>* _left;
AVLTreeNode<K, V>* _right;
AVLTreeNode<K, V>* _parent;
pair<K, V> _kv;
int _bf;
AVLTreeNode(const pair<K,V>& kv)
:_left(nullptr)
,_right(nullptr)
,_parent(nullptr)
,_kv(kv)
,_bf(0)
{
}
};首先我们相比二叉平衡树不一样的地方在于我们需要加入一个parent指针，这个指针用来记录每个节点的父节点，因为后期调整平衡因子需要从新增节点往上查找。然后就是我们在map中见到的键值对pair了，同时还有一个变量是平衡因子。然后我们给树的节点写一个构造函数，在构造函数中我们的参数为pair，然后在初始化列表中将left,right,parent指针初始化为nullptr，然后将节点中的键值对用参数初始化，并且每个新节点的平衡因子都是0.
下面我们实现AVL树的主体：
template<class K,class V>
class AVLTree
{
typedef AVLTreeNode<K, V> Node;
public:
private:
Node* _root = nullptr;
};我们将AVL树的节点typedef一下，这样在后面的使用会更方便，然后树中有一个根节点，我们给一个缺省参数让根节点为空，下面我们就实现AVL树的插入，插入的前面和二叉搜索树一样，下面的代码我先放出来：
bool insert(const pair<K, V>& kv)
{
if (_root == nullptr)
{
_root = new Node(kv);
return true;
}
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
if (cur->_kv.first < kv.first)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_kv.first > kv.first)
{
parent = cur;
cur = cur->_left;
}
else
{
return false;
}
}
cur = new Node(kv);
if (parent->_kv.first < kv.first)
{
parent->_right = cur;
}
else
{
parent->_left = cur;
}
cur->_parent = parent;
//开始控制平衡因子
while (parent)
{
if (parent->_left == cur)
{
parent->_bf--;
}
else if (parent->_right == cur)
{
parent->_bf++;
}
if (parent->_bf == 0)
{
//已经平衡了
break;
}
else if (parent->_bf == 1 || parent->_bf == -1)
{
//需要继续向上调节
parent = parent->_parent;
cur = cur->_parent;
}
else if (parent->_bf == 2 || parent->_bf == -2)
{
//需要旋转控制，旋转的目的是降低高度+平衡，所以旋转完毕后退出循环。
//首先是单纯右边高，需要左单旋
if (parent->_bf == 2 && cur->_bf == 1)
{
RotateL(parent);
}
//如果是单纯左边高，需要右单旋
else if (parent->_bf == -2 && cur->_bf == -1)
{
RotateR(parent);
}
//如果是整体左边高，并且左边的第一个节点的右子树高，就需要先左单旋，再右单旋
else if (parent->_bf == -2 && cur->_bf == 1)
{
RotateLR(parent);
}
//如果整体右边高，但是右边第一个节点的左边高，就需要先右单旋，再左单旋
else if (parent->_bf == 2 && cur->_bf == -1)
{
RotateRL(parent);
}
else
{
assert(false);
}
//当任何一个旋转结束了当前树都会平衡，所以需要直接退出循环
break;
}
else
{
assert(false);
}
}
return true;
}上面是AVL树的插入实现，下面我们一点一点代码慢慢讲解：
bool insert(const pair<K, V>& kv)
{
if (_root == nullptr)
{
_root = new Node(kv);
return true;
}
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
if (cur->_kv.first < kv.first)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_kv.first > kv.first)
{
parent = cur;
cur = cur->_left;
}
else
{
return false;
}
}
cur = new Node(kv);
if (parent->_kv.first < kv.first)
{
parent->_right = cur;
}
else
{
parent->_left = cur;
}首先和我们实现二叉搜索树一样，先判断根节点是否为空，如果根节点为空则需要直接将新增的节点给根节点，然后返回true即可。接下来需要一个用于遍历的节点cur和parent节点，因为我们在遍历的时候最后cur会变成空指针，这个时候cur已经失效了即使让cur开一个新节点也没法链接到cur的父节点，所以我们需要一个parent节点来记录遍历的那个节点的父节点。接下来就是二叉搜索树的正常步骤，如果要插入的元素比当前节点的元素大就去当前节点的右子树寻找，如果要插入的元素比当前节点的元素小就去当前节点的左子树找，如果碰到相同元素我们就返回false，当出循环后我们让cur指向新节点，并且判断要插入的节点是在父节点的左边还是右边，以上都是二叉搜索树的内容，下面我们进入AVL树的内容：
while (parent)
{
if (parent->_left == cur)
{
parent->_bf--;
}
else if (parent->_right == cur)
{
parent->_bf++;
}
if (parent->_bf == 0)
{
//已经平衡了
break;
}
else if (parent->_bf == 1 || parent->_bf == -1)
{
//需要继续向上调节
parent = parent->_parent;
cur = cur->_parent;
}首先我们控制平衡因子必须以parent节点作为循环条件，因为在从新增节点到节点的祖先的遍历中parent节点最先有可能变成nullptr(走到根节点就变成了nullptr).下面我们用图进行讲解：
由于新增节点的位置不同所以平衡因子的改变也不同，就比如上图中有的节点平衡因子变成了2已经不平衡了，有的平衡因子变成了0变的平衡了，那么如何改变平衡因子呢，下面我们给出结果：
1.如果我们新增的节点是父节点的左子树，那么父节点的平衡因子就-1，如果我们新增的节点是父节点的右子树，那么父节点的平衡因子就+1.
2.如果我们的父节点的平衡因子由于新增节点变成0了，这就说明原先这个父节点是不平衡的，新增节点后变的平衡了这个时候满足AVL树的要求。如第二种图。
3.如果我们的父节点的平衡因子由于新增节点变成1或者-1了，这就说明原先这个父节点是0也就是平衡的，经过新增节点后才变的不平衡，但是这个时候的父节点高度差没有超过1所以当前这个父节点不需要管了，我们要去这个父节点的父节点查看平衡因子是否满足要求，只有当某个祖先的平衡因子变成2或者-2这个时候就需要通过旋转使这棵树更加的平衡。就如第一张图一样，新增节点插入后9的平衡因子满足要求，但是8的平衡因子不满足要求了所以需要调整。
知道了以上三点大家应该就可以看懂代码了，当新增节点为父节点的左边我们就让父节点的平衡因子-1，当新增节点为父节点的右边我们就让父节点的平衡因子+1.修改为当前平衡因子后我们需要考虑向上更新平衡因子，当新增后父节点的平衡因子为0时我们就不需要调整了直接退出循环即可，当新增后父节点的平衡因子为1或者-1时，我们就需要往上继续更新平衡因子，继续看下面的代码：
else if (parent->_bf == 2 || parent->_bf == -2)
{
//需要旋转控制，旋转的目的是降低高度+平衡，所以旋转完毕后退出循环。
//首先是单纯右边高，需要左单旋
if (parent->_bf == 2 && cur->_bf == 1)
{
RotateL(parent);
}
//如果是单纯左边高，需要右单旋
else if (parent->_bf == -2 && cur->_bf == -1)
{
RotateR(parent);
}
//如果是整体左边高，并且左边的第一个节点的右子树高，就需要先左单旋，再右单旋
else if (parent->_bf == -2 && cur->_bf == 1)
{
RotateLR(parent);
}
//如果整体右边高，但是右边第一个节点的左边高，就需要先右单旋，再左单旋
else if (parent->_bf == 2 && cur->_bf == -1)
{
RotateRL(parent);
}
else
{
assert(false);
}
//当任何一个旋转结束了当前树都会平衡，所以需要直接退出循环
break;
}
else
{
assert(false);
}当新增后平衡因子为2或者为-2时，我们就需要旋转控制了，下面我们讲解四种旋转的方式：
第一种：当新增节点后这棵树的纯粹的右边的高度高于左边的高度时，需要左单旋（就是将右边高的节点旋转到左边）：
如上图所示，首先我们要明白左单旋的意义，左单旋就是为了降低高度并且让树变的平衡，比如上图中把30这个根节点放到60的左边就会降低一层的高度，那么为了将30变成60的子树必须让30及30的所有子树都小于60才可以，所有选择让60的左树去当30的右树（因为60的左树一定是小于60大于30的，为了放入60的左树正好满足小于60的要求），然后再将修改后的30这棵树放到60的左边。理解了如何单旋后我们看当上图中h等于0时新增1节点在哪个位置一定会引发旋转，并且旋转后一定能降低高度，经过画图得知只有新增节点在C的位置才一定会引发旋转并且旋转一定可以降低高度，这也验证了我们上面所说的只有纯粹的右边高度高时才需要左单旋，当h==0,新增节点在60的左边这个时候60的平衡因子为-1说明60的左边高度高，所以不满足我们的要求旋转后也没有降低高度。当h==0新增节点在60的右边这个时候60的平衡因子为1,30的平衡因子为2满足我们的要求，旋转后也成功降低了高度。
下面我们看看当h==1的情况：
当h==1时我们同样在C的位置插入，不管插入到C的左子树还是右子树，根节点的平衡因子都为2并且根节点的右子树的平衡因子都为1，所以在C的位置插入节点都会引发旋转。
下面我们看h==2的情况：
下面是在C的任意位置插入都会引发旋转的图：
我们可以看到不管在C的哪个位置插入，最终根节点的平衡因子都是2，根节点右边的平衡因子都是1，有了上面的图相信大家知道了左单旋以及左单旋的条件，只有当父节点的平衡因子为2并且cur的平衡因子为1才会左单旋，因为这样的数是纯粹的右边高度高。下面是左单旋的代码：
void RotateL(Node* parent)
{
Node* subR = parent->_right;
Node* subRL = subR->_left;
Node* ppnode = parent->_parent;
parent->_right = subRL;
if (subRL)
{
subRL->_parent = parent;
}
subR->_left = parent;
parent->_parent = subR;
if (ppnode == nullptr)
{
_root = subR;
_root->_parent = nullptr;
}
else
{
if (ppnode->_left == parent)
{
ppnode->_left = subR;
}
else
{
ppnode->_right = subR;
}
subR->_parent = ppnode;
}
parent->_bf = subR->_bf = 0;
}要看上面的代码我们单独画一张左单旋的图为例：
以上图为例，我们需要保存父节点的右边节点以及父节点右边节点的左边节点，我们将父节点的右边节点记录为subR,将fsubR的左边节点记录为subRL,然后我们还需要保存父节点的父节点，因为有可能我们旋转的不是一整颗树，而是一棵树的一个子树，我们先让父节点的右边连接上subRL,因为有可能subRL这个节点是空，所以我们需要先判断subRL不为空然后让subRL的父节点连接到parent上，然后再将subR的左边连接parent，同样将parent的父节点连接到subR,这里就体现了我们提前保存父节点的父节点的好处（因为parent的父节点变了）。这个时候我们就该判断ppnode是否为空了，如果ppnode为空就说明subR就是根节点了，如果不为空说明我们旋转的只是一颗子树，我们需要判断ppnode的哪边链接着以前的父节点，然后将subR正确链接，同时在最后我们还需要将subR链接到ppnode上，这样就完成了旋转，因为旋转后parent和subR的平衡因子都变成0了，所以我们记得将这两个的平衡因子改为0.
下面是右单旋的图，右单旋大体与左单旋一模一样，只不过右单旋是纯粹的左边高度高才会右单旋，并且右单旋的条件为parent的平衡因子为-2，cur的平衡因子为-1：
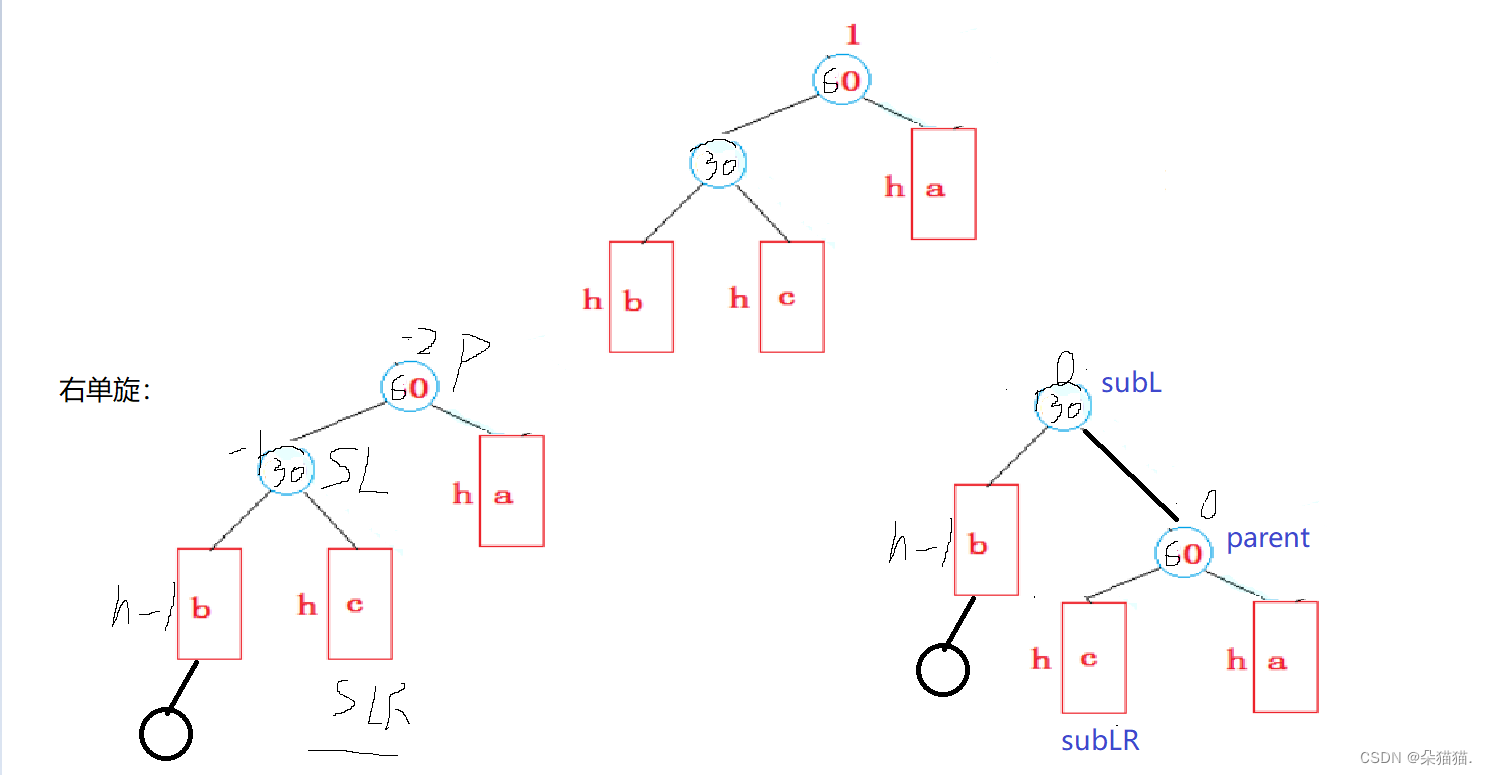
右单旋一定是在b的位置插入才会一定引发旋转，下面看代码：
void RotateR(Node* parent)
{
Node* subL = parent->_left;
Node* subLR = subL->_right;
Node* ppnode = parent->_parent;
parent->_left = subLR;
if (subLR)
{
subLR->_parent = parent;
}
subL->_right = parent;
parent->_parent = subL;
if (ppnode == nullptr)
{
_root = subL;
_root->_parent = nullptr;
}
else
{
if (ppnode->_left == parent)
{
ppnode->_left = subL;
}
else
{
ppnode->_right = subL;
}
subL->_parent = ppnode;
}
parent->_bf = subL->_bf = 0;
}从代码可以看到右单旋与左单旋的思路一模一样，只不过旋转需要移动的节点变了而已，大家对照着图和代码完全可以看明白（当然是已经看懂左单旋的前提下）
下面我们分析双旋的情况：
首先触发双旋的条件一定是上图中60这个节点的变化，当h==0时说明60这个节点就是新增节点，这个时候一个单旋已经搞不定了，必须先将parent的左节点左单旋，再将整个parent右旋，并且当h==0的时候新增节点的平衡因子默认为0，这个时候parent,subL,subLR的平衡因子都为0.
下面我们再看h==1的情况：
h==1有两种情况，要不在60的左树插入，要不在60的右树插入，不同的是如果插入在60的左树那么parent的平衡因子会变成1，其他两个节点的平衡因子还是0.当插入的节点在60的右边，那么只有subL的平衡因子变成-1,其他的平衡因子变成0，下面我们写先左旋再右旋的代码：
void RotateLR(Node* parent)
{
Node* subL = parent->_left;
Node* subLR = subL->_right;
int bf = subLR->_bf;
RotateL(parent->_left);
RotateR(parent);
if (bf == 1)
{
parent->_bf = 0;
subL->_bf = -1;
subLR->_bf = 0;
}
else if (bf == -1)
{
parent->_bf = 1;
subL->_bf = 0;
subLR->_bf = 0;
}
else if (bf == 0)
{
parent->_bf = 0;
subL->_bf = 0;
subLR->_bf = 0;
}
else
{
assert(false);
}
}首先我们要记住，要满足先左旋再右旋的条件，一定是这棵树或者这颗子树的整体高度是左边高度高，并且左边的第一个节点的右边高度高，因为我们先左旋就是将这个左边第一个节点的右边左旋（因为右边高度高），这个时候整体都变成了纯粹的左边高，如果是纯粹的左边高我们再使用右旋，所以这就是先左旋再右旋的由来。条件一定是：parent的平衡因子为-2（代表整体左边高），cur的平衡因子为1（代表左边的第一个节点右边高度高）。首先我们保存parent的左边节点也就是subL,然后保存这个左边节点的右边节点subLR,并且我们要记录这个subLR的平衡因子，因为我们前面说过只有这个位置插入才会发生旋转，并且插入到这个位置的左树还是右树后面的平衡因子都是不一样的，所以我们先保存这个节点的平衡因子，先左旋parent的左边节点后，再整体右旋，然后判断（用平衡因子判断）新增的节点在subLR的左边还是右边，如果为1说明在右边，我们要将平衡因子更新，这里要对照着图，发现subL的平衡因子变成-1，如果为-1说明在左边parent的平衡因子变成1，如果等于0说明自己就是新增的节点，然后我们的先左旋再右旋就结束了。
下面是先右旋再左旋：
同样我们先以h==0为例，如果h==0那么60就是新增的节点，这个时候旋转完后subRL,subR和parent的平衡因子都为0.
当h==1同样有两种，其实也就是从b插入或者从c插入，在这两个位置都会引发双旋，只不过现在h==1无b,c这两个位置而已，在60的左边插入和60的右边插入结果都是不一样的，下面我们直接看代码：
void RotateRL(Node* parent)
{
Node* subR = parent->_right;
Node* subRL = subR->_left;
int bf = subRL->_bf;
RotateR(parent->_right);
RotateL(parent);
if (bf == 1)
{
parent->_bf = -1;
subR->_bf = 0;
subRL->_bf = 0;
}
else if (bf == -1)
{
parent->_bf = 0;
subR->_bf = 1;
subRL->_bf = 0;
}
else if (bf == 0)
{
parent->_bf = 0;
subR->_bf = 0;
subRL->_bf = 0;
}
else
{
assert(false);
}
}与先左旋再右旋不一样的地方在于平衡因子的要选择的节点，因为要满足先右旋再左旋的条件，所以这棵树一定是整体右边高度高，右边的第一个节点左边高度高，也就是parent的平衡因子为2（说明整体右边高）并且cur的平衡因子为-1（说明右边第一个节点的左边高度高）。我们保存右边第一个节点和右边第一个节点的左边节点，然后保存subRL的平衡因子，然后先右旋parent的右边节点，然后整体左旋。旋转完毕后继续更新平衡因子即可。所有的else我们都用assert报错，因为有可能一棵树一开始的平衡因子就有问题。当我们旋转完成这棵树一定是高度降低并且平衡了，所以我们直接退出循环返回true即可。
以上就是AVL树的插入，除了erase接口其他接口都与搜索二叉树一样，下面我们将代码测试一下：
namespace AVLTreeK
{
template<class K>
struct AVLTreeNode
{
AVLTreeNode<K>* _left;
AVLTreeNode<K>* _right;
AVLTreeNode<K>* _parent;
K _kv;
int _bf;
AVLTreeNode(const K& kv)
:_left(nullptr)
, _right(nullptr)
, _parent(nullptr)
, _kv(kv)
, _bf(0)
{
}
};
template<class K>
class AVLTree
{
typedef AVLTreeNode<K> Node;
public:
void Inorder()
{
_Inorder(_root);
}
void _Inorder(Node* root)
{
if (root == nullptr)
{
return;
}
cout << root->_kv << " ";
_Inorder(root->_left);
_Inorder(root->_right);
}
bool insert(const K& kv)
{
if (_root == nullptr)
{
_root = new Node(kv);
return true;
}
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
if (cur->_kv < kv)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_kv > kv)
{
parent = cur;
cur = cur->_left;
}
else
{
return false;
}
}
cur = new Node(kv);
if (parent->_kv < kv)
{
parent->_right = cur;
}
else
{
parent->_left = cur;
}
cur->_parent = parent;
//开始控制平衡因子
while (parent)
{
if (parent->_left == cur)
{
parent->_bf--;
}
else if (parent->_right == cur)
{
parent->_bf++;
}
if (parent->_bf == 0)
{
//已经平衡了
break;
}
else if (parent->_bf == 1 || parent->_bf == -1)
{
//需要继续向上调节
parent = parent->_parent;
cur = cur->_parent;
}
else if (parent->_bf == 2 || parent->_bf == -2)
{
//需要旋转控制，旋转的目的是降低高度+平衡，所以旋转完毕后退出循环。
//首先是单纯右边高，需要左单旋
if (parent->_bf == 2 && cur->_bf == 1)
{
RotateL(parent);
}
//如果是单纯左边高，需要右单旋
else if (parent->_bf == -2 && cur->_bf == -1)
{
RotateR(parent);
}
//如果是整体左边高，并且左边的第一个节点的右子树高，就需要先左单旋，再右单旋
else if (parent->_bf == -2 && cur->_bf == 1)
{
RotateLR(parent);
}
//如果整体右边高，但是右边第一个节点的左边高，就需要先右单旋，再左单旋
else if (parent->_bf == 2 && cur->_bf == -1)
{
RotateRL(parent);
}
else
{
assert(false);
}
//当任何一个旋转结束了当前树都会平衡，所以需要直接退出循环
break;
}
else
{
assert(false);
}
}
return true;
}
private:
void RotateL(Node* parent)
{
Node* subR = parent->_right;
Node* subRL = subR->_left;
Node* ppnode = parent->_parent;
parent->_right = subRL;
if (subRL)
{
subRL->_parent = parent;
}
subR->_left = parent;
parent->_parent = subR;
if (ppnode == nullptr)
{
_root = subR;
_root->_parent = nullptr;
}
else
{
if (ppnode->_left == parent)
{
ppnode->_left = subR;
}
else
{
ppnode->_right = subR;
}
subR->_parent = ppnode;
}
parent->_bf = subR->_bf = 0;
}
void RotateR(Node* parent)
{
Node* subL = parent->_left;
Node* subLR = subL->_right;
Node* ppnode = parent->_parent;
parent->_left = subLR;
if (subLR)
{
subLR->_parent = parent;
}
subL->_right = parent;
parent->_parent = subL;
if (ppnode == nullptr)
{
_root = subL;
_root->_parent = nullptr;
}
else
{
if (ppnode->_left == parent)
{
ppnode->_left = subL;
}
else
{
ppnode->_right = subL;
}
subL->_parent = ppnode;
}
parent->_bf = subL->_bf = 0;
}
void RotateLR(Node* parent)
{
Node* subL = parent->_left;
Node* subLR = subL->_right;
int bf = subLR->_bf;
RotateL(parent->_left);
RotateR(parent);
if (bf == 1)
{
parent->_bf = 0;
subL->_bf = -1;
subLR->_bf = 0;
}
else if (bf == -1)
{
parent->_bf = 1;
subL->_bf = 0;
subLR->_bf = 0;
}
else if (bf == 0)
{
parent->_bf = 0;
subL->_bf = 0;
subLR->_bf = 0;
}
else
{
assert(false);
}
}
void RotateRL(Node* parent)
{
Node* subR = parent->_right;
Node* subRL = subR->_left;
int bf = subRL->_bf;
RotateR(parent->_right);
RotateL(parent);
if (bf == 1)
{
parent->_bf = -1;
subR->_bf = 0;
subRL->_bf = 0;
}
else if (bf == -1)
{
parent->_bf = 0;
subR->_bf = 1;
subRL->_bf = 0;
}
else if (bf == 0)
{
parent->_bf = 0;
subR->_bf = 0;
subRL->_bf = 0;
}
else
{
assert(false);
}
}
private:
Node* _root = nullptr;
};
}测试的时候我们以K模型测试，下面是测试样例：
void test()
{
AVLTreeK::AVLTree<int> at;
int a[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16,14 };
int b[] = { 16, 3, 7, 11, 9, 26, 18, 14, 15 };
for (auto& e : a)
{
at.insert(e);
}
at.Inorder();
}我们自己画一个经过旋转后的图与前序遍历结果看是否一样：
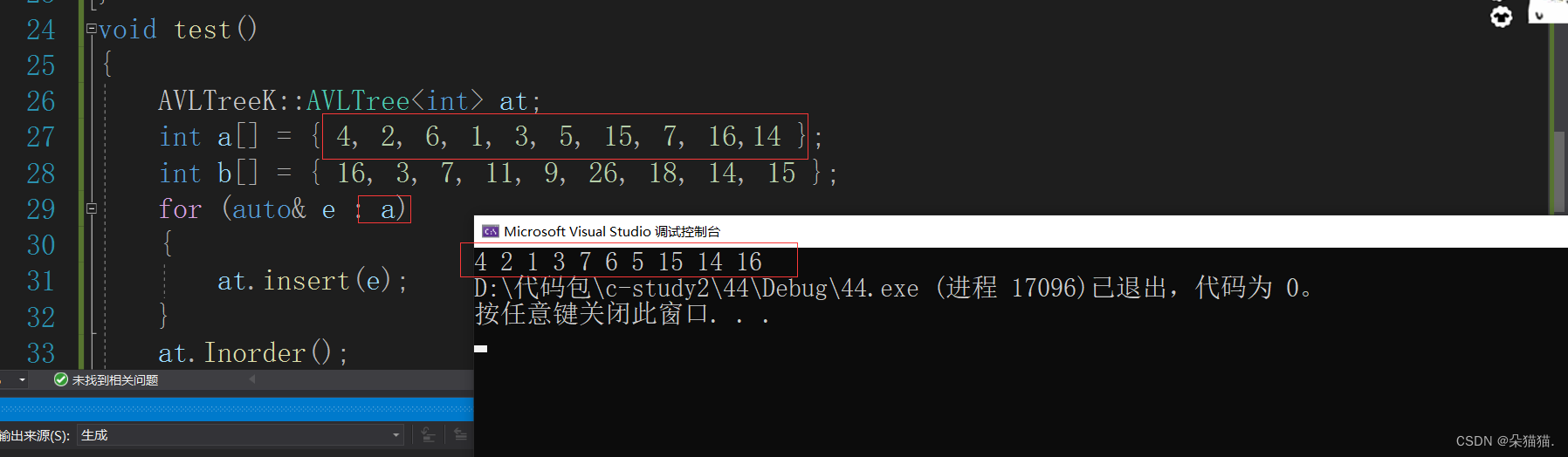
我们可以看到答案是正确的，以上就是我们AVL树的所有内容了。
