思路真的和他很像，但是我不太会写容斥，只写过几道板子题

而且有个地方不知道怎么处理，就是容斥原理的F函数里面怎么求多个路径的边的并集

这里是用状压处理的

该学学容斥的写法了QwQ

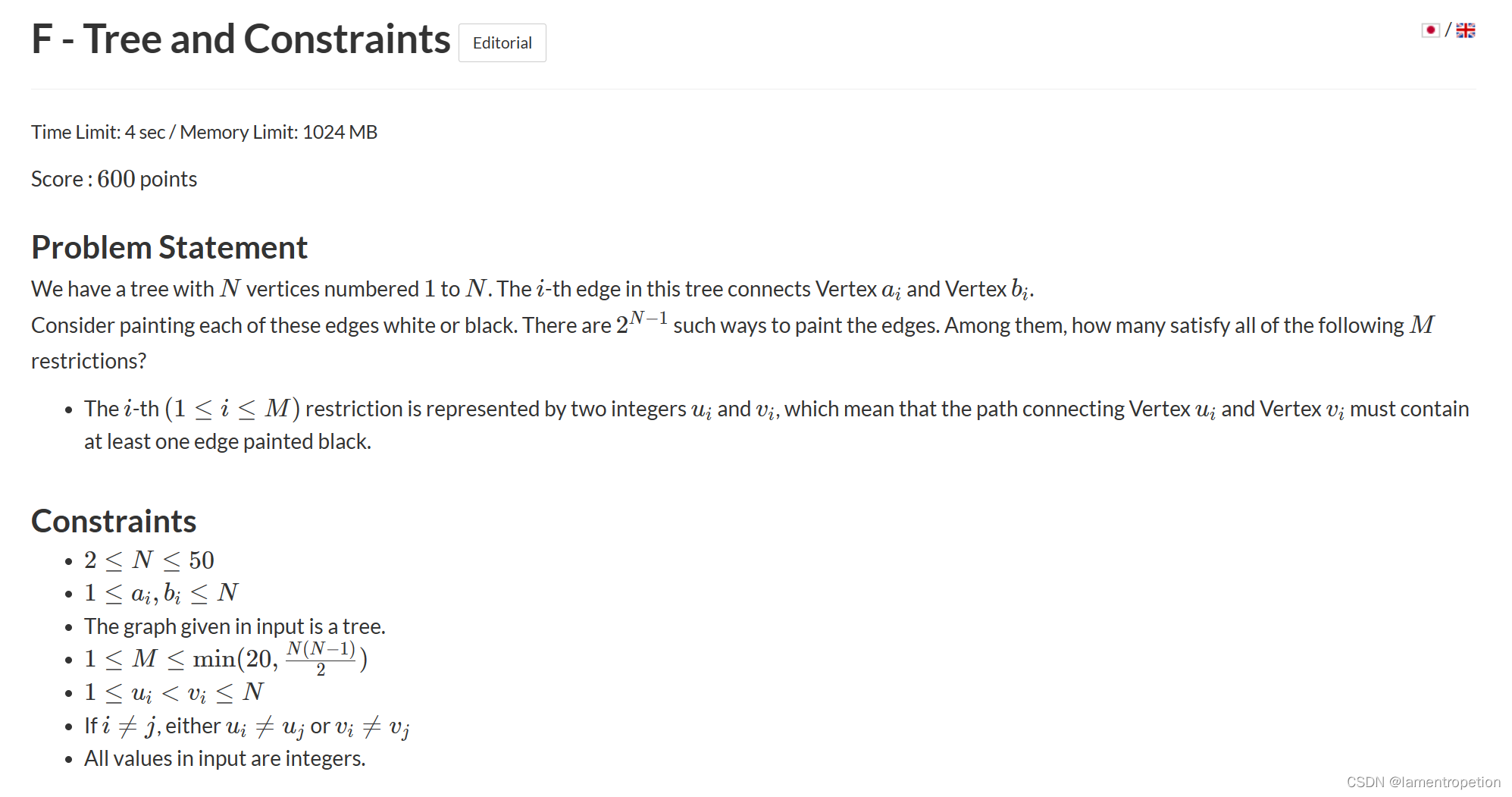
F - Tree and Constraints (atcoder.jp)

题意：

给定一棵树，可以给每一条边都染成黑色或白色，给定Q个要求，每个要求都包含两个数u和v，表示u和v这条路径中至少需要一条边被染成黑色，要同时满足这Q个要求，问染色方案数

 思路：

一开始的想法是这样的：

 

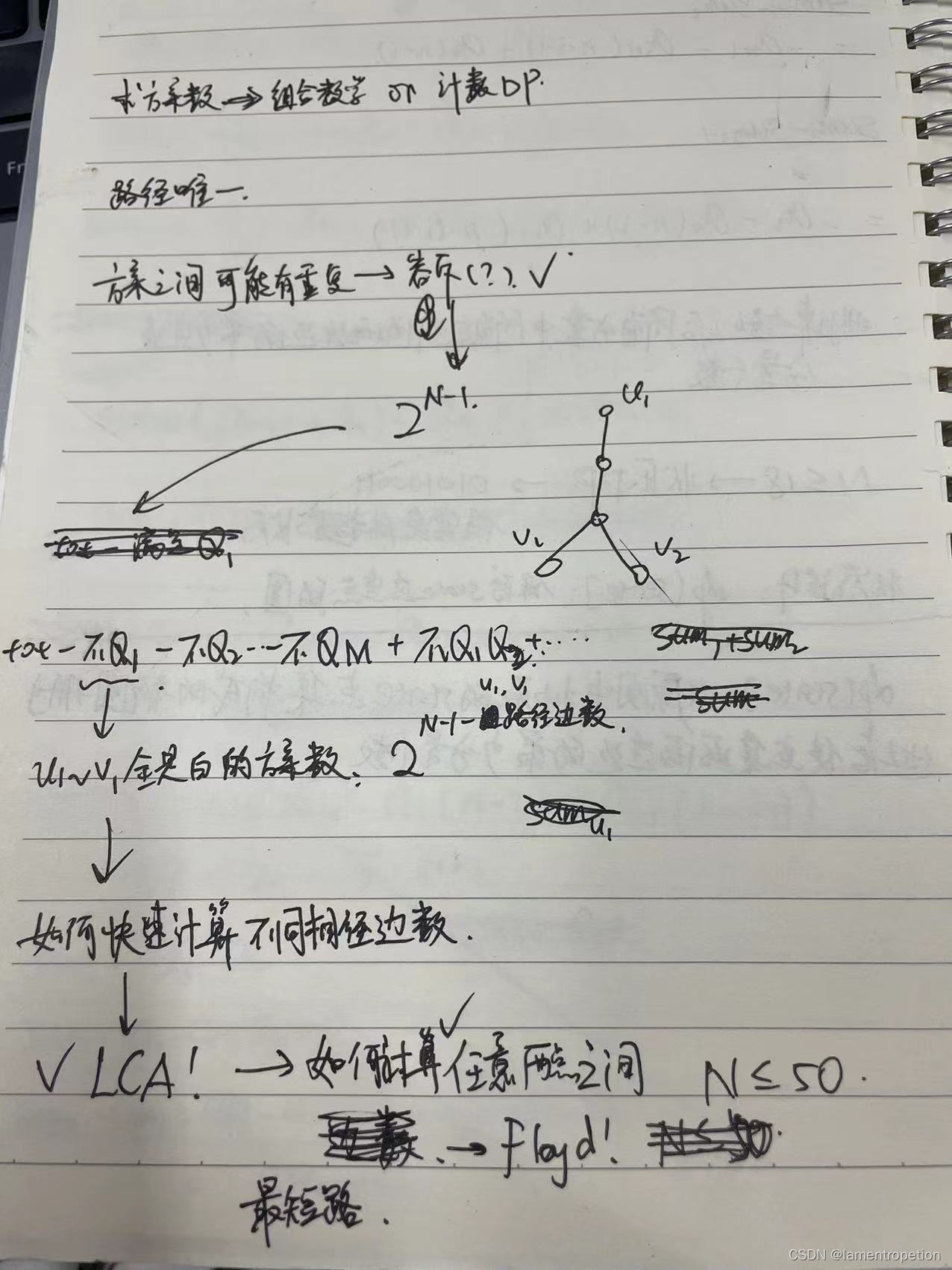
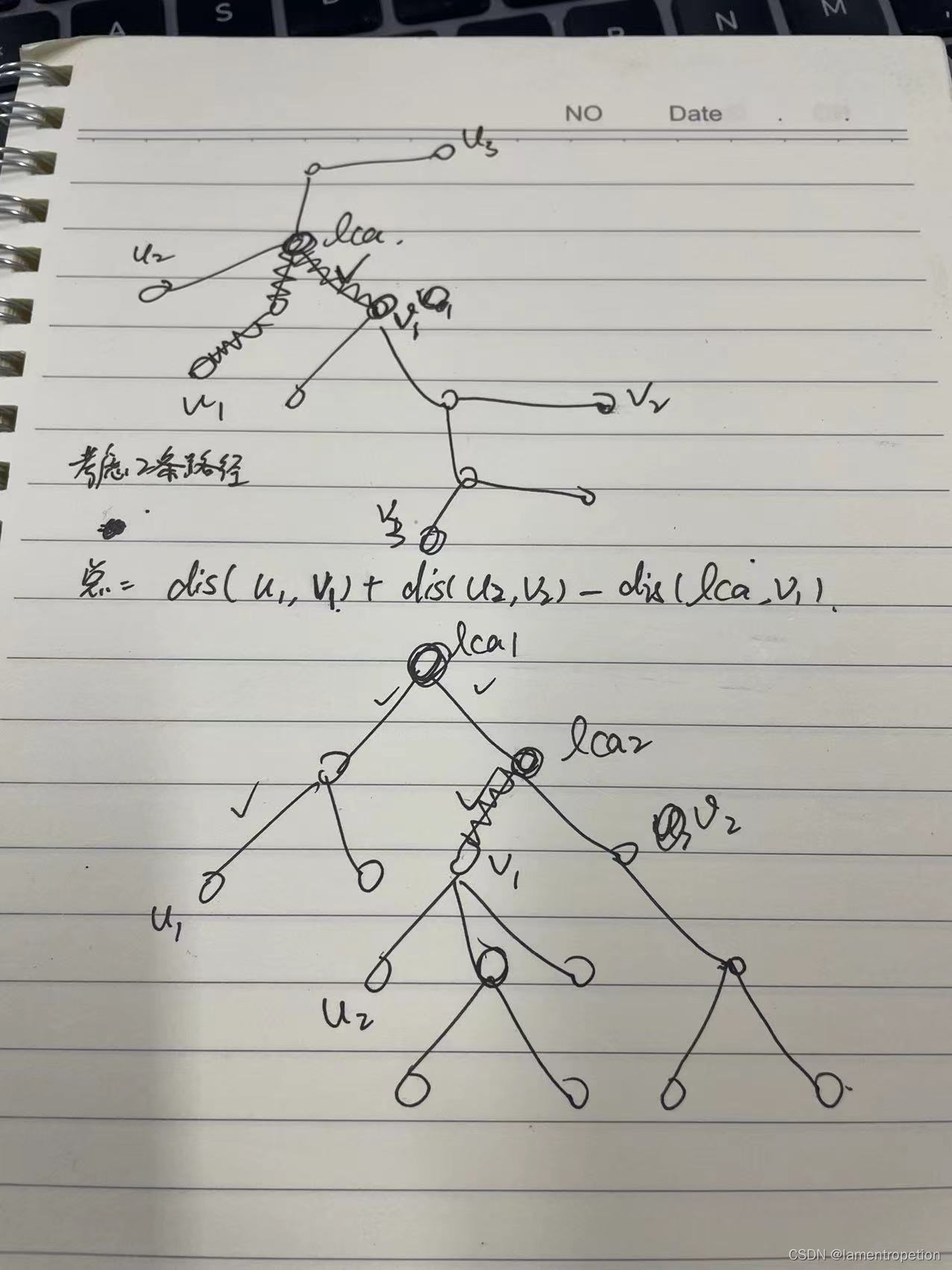
对于计算多条路径的边集的并集，本来想着用Floyd和Lca处理，结果发现好像不太行

对于容斥，我们计算的是所有情况-不合法的情况的并集

即2^(N-1)-Q1-Q2-....+Q12+Q13+....

 所以我们面临两个问题：

如何计算一条路径中的边权和，这个可以Floyd（当然也可以不用）

如何计算多条路径的边集的并集

这里用状压处理

先dfs预处理出树上结点前缀异或和

然后u和v的路径中的边集就是pre[u]^pre[v]

其实是点集，但是也可以看成边集，数量是一样的

所以F函数里面就可以计算一个选的状态的贡献了

直接或起来，然后或起来的结果的1的个数就是边集的并集大小

该状态对应的组合数就是(1ll<<(N-1-__builtin_popcountll(sum)))

如果该状态个数是奇数就需要*-1ll

累加即可

Code：

#include <bits/stdc++.h>

#define int long long

using namespace std;

const int mxn=1e2+10;
const int mxe=1e2+10;

struct ty{
    int to,next;
}edge[mxe<<2];

int N,M,u,v,x,y,tot=0;
int head[mxn],pre[mxn],st[mxn];

void add(int u,int v){
    edge[tot].to=v;
    edge[tot].next=head[u];
    head[u]=tot++;
}
void G_init(){
    tot=0;
    for(int i=0;i<=N;i++){
        head[i]=-1;
    }
}
void dfs(int u,int fa){
    for(int i=head[u];~i;i=edge[i].next){
        if(edge[i].to==fa) continue;
        pre[edge[i].to]=pre[u]|(1ll<<(edge[i].to-1));
        dfs(edge[i].to,u);
    }
}
int F(int x){
    int cnt=__builtin_popcountll(x);
    int sum=0,res=0;
    for(int j=0;j<M;j++){
        if((x>>j)&1) sum|=st[j];
    }
    res=(1ll<<(N-1-__builtin_popcountll(sum)));
    if(cnt&1) res*=(-1ll);
    return res;
}
void solve(){
    cin>>N;
    G_init();
    for(int i=1;i<=N-1;i++){
        cin>>u>>v;
        add(u,v);
        add(v,u);
    }
    dfs(1,-1);
    cin>>M;
    for(int i=0;i<M;i++){
        cin>>x>>y;
        st[i]=pre[x]^pre[y];
    }
    int ans=0;
    for(int x=0;x<(1<<M);x++) ans+=F(x);
    cout<<ans<<'\n';
}
signed main(){
    ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
    int __=1;//cin>>__;
    while(__--)solve();return 0;
}