目录
第1关:0/1背包问题
任务描述:
相关知识:
分支限界法基本思想:
常见的分支限界法:
示例:0/1背包问题
对于0/1背包的优化:
题目描述:
编程要求:
测试说明:
第2关:旅行商问题
任务描述:
相关知识:
问题描述:
问题分析:
编程要求:
测试说明:
第1关:0/1背包问题
任务描述:
本关任务:分支限界法;
相关知识:
为了完成本关任务,你需要掌握:0/1背包问题;
分支限界法基本思想:
分支限界法是求解纯整数规划或混合整数规划问题的经典方法,在上世纪六十年代由Land Doig和Dakin等人提出。这种方法灵活且便于用计算机求解,目前已经成功运用于求解生产进度问题、旅行推销员问题、工厂选址问题、背包问题及分配问题等。算法基本思想如下:
- 以广度优先或以最小耗费(最大效益)优先的方式搜索问题的解空间树。
- 分支限界法中,每一个活结点只有一次机会成为扩展结点,活结点一旦成为扩展结点,就一次性产生其所有儿子结点,其中导致不可行解或导致非最优解的儿子结点被舍弃,其余儿子结点被加入活结点表中。
- 然后从活结点表中取下一结点成为当前扩展结点。
- 重复上述结点扩展过程,直至到找到所需的解或活结点表为空时为止。
常见的分支限界法:
队列式分支限界法 按照队列先进先出(FIFO)原则选取下一个结点为扩展结点 从活结点表中取出结点的顺序与加入结点的顺序相同,因此活结点表的性质与队列相同
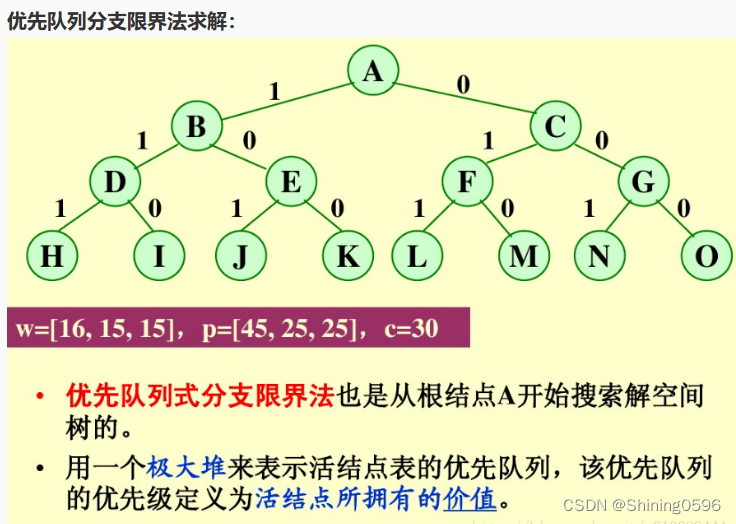
优先队列分支限界法(代价最小或效益最大) 每个结点都有一个对应的耗费或收益,以此决定结点的优先级 从优先队列中选取优先级最高的结点成为当前扩展结点 如果查找一个具有最小耗费的解:则活结点表可用小顶堆来建立,下一个扩展结点就是具有最小耗费的活结点 如果希望搜索一个具有最大收益的解:则可用大顶堆来构造活结点表,下一个扩展结点是具有最大收益的活结点
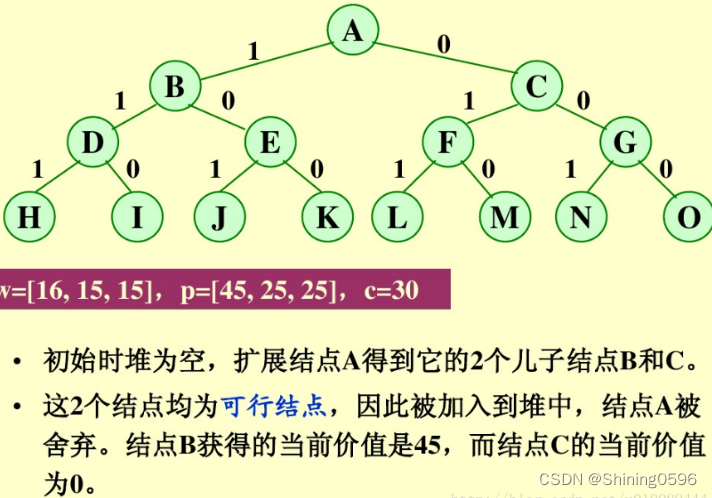
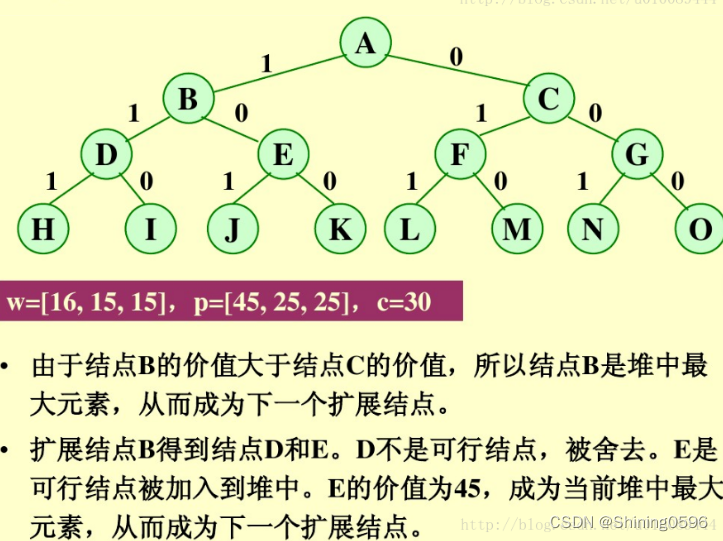
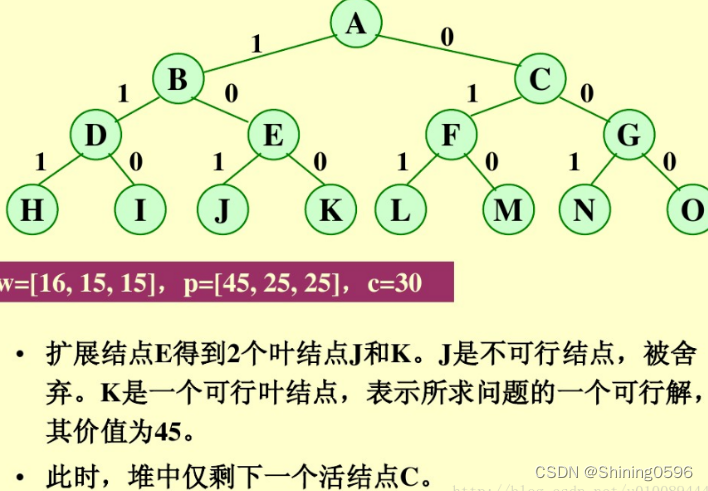
示例:0/1背包问题
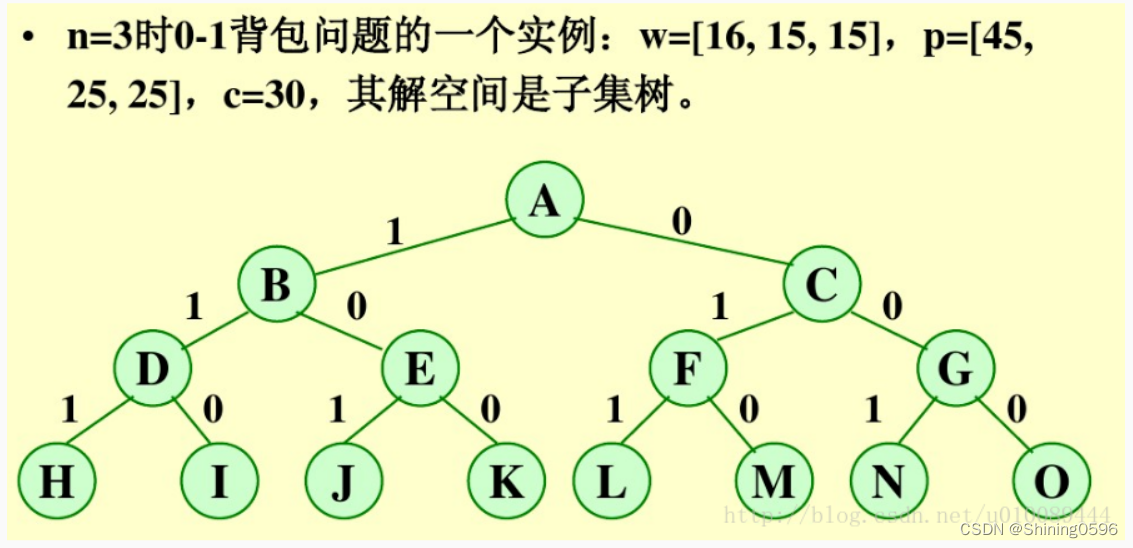
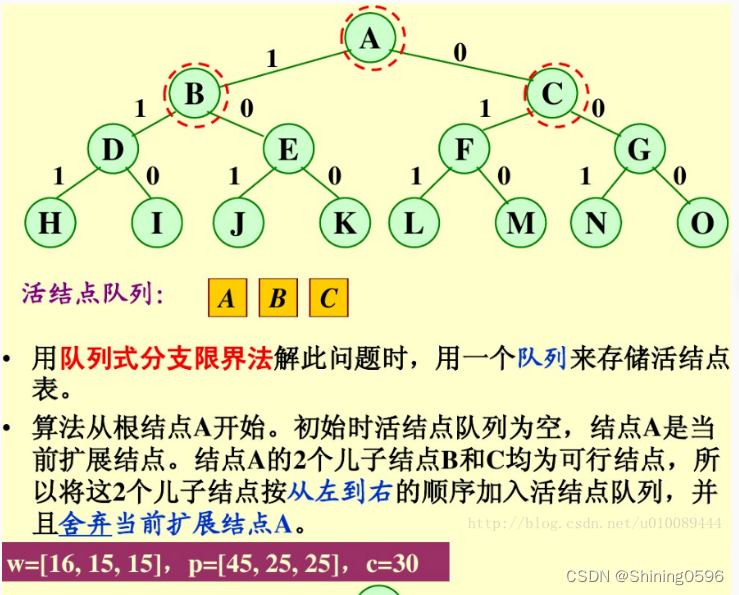
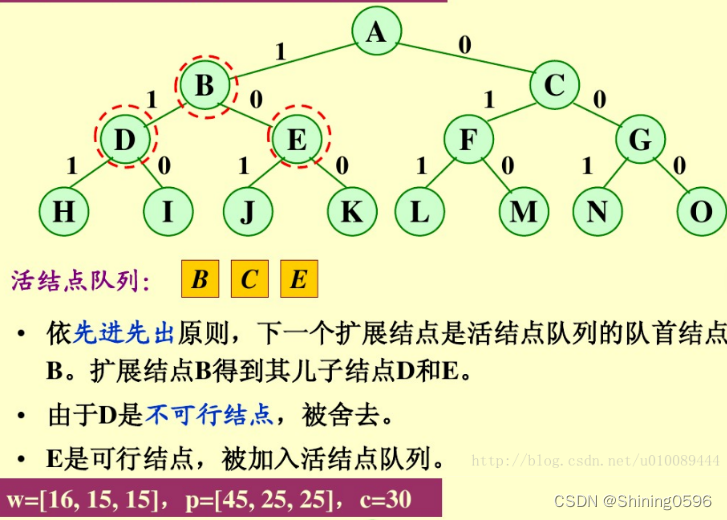
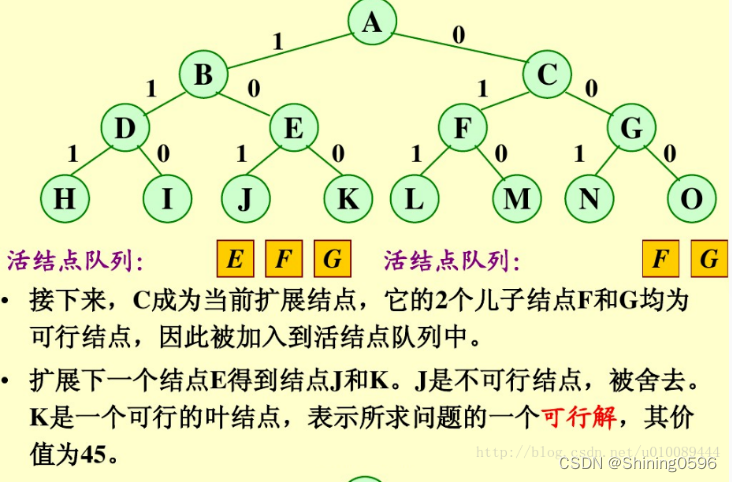
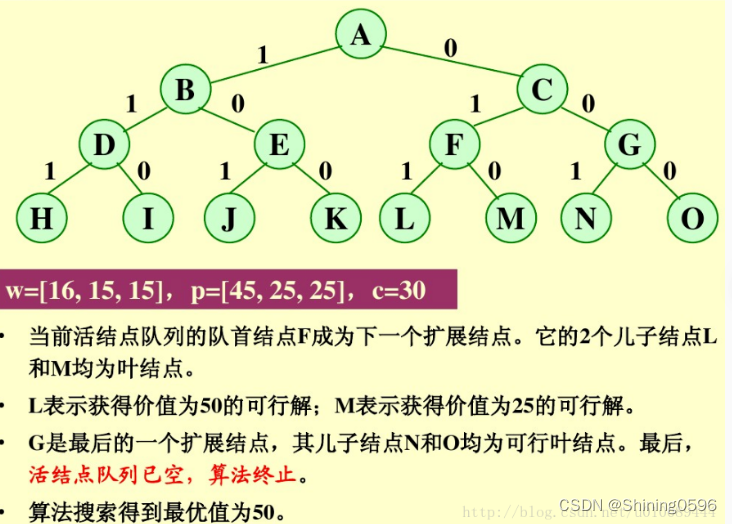
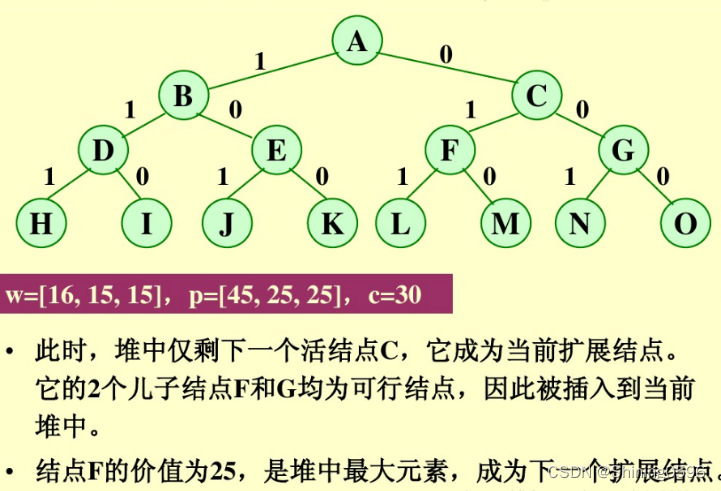
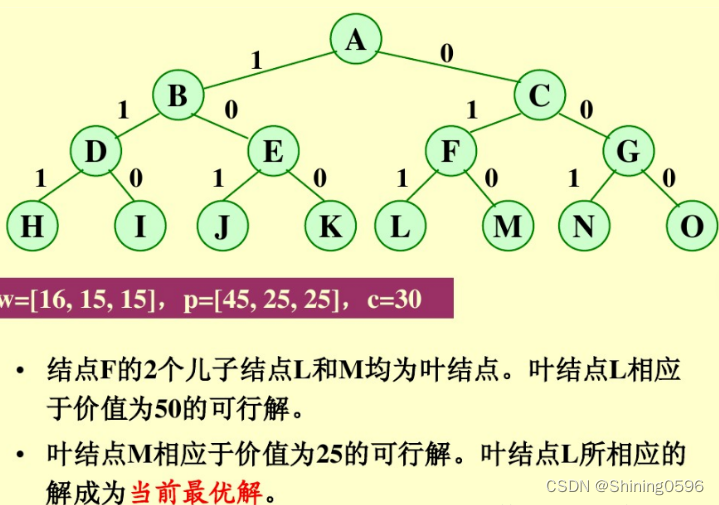
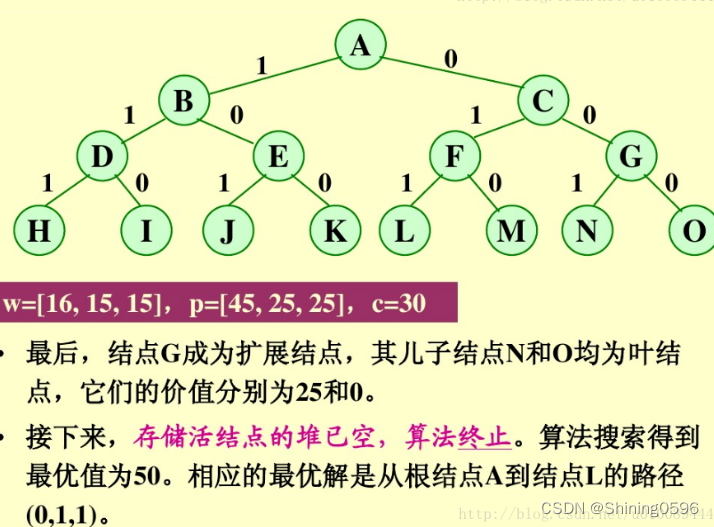
对于0/1背包的优化:
首先,要对输入数据进行预处理,将各物品依其单位重量价值从大到小进行排列。在优先队列分支限界法中,节点的优先级由已装袋的物品价值加上剩下的最大单位重量价值的物品装满剩余容量的价值和。 算法首先检查当前扩展结点的左儿子结点的可行性。如果该左儿子结点是可行结点,则将它加入到子集树和活结点优先队列中。当前扩展结点的右儿子结点一定是可行结点,仅当右儿子结点满足上界约束时才将它加入子集树和活结点优先队列。当扩展到叶节点时为问题的最优值。
题目描述:
0-1背包问题:给定n种物品和一背包。物品i的重量是wi, 其价值为Vi, 背包的容量为C。问应如何选择装入背包中的物品,使得装入背包中物品的总价值最大?在选择装入背包的物品时,对每种物品i可以选择这个物品的一部分。
编程要求:
根据提示,在右侧编辑器补充代码,树的层次遍历。
输入: 通过文件读入,第一行包括两个整数n和c,代表物品数和背包容量,接下来的n行每行包括两个整数,$w[i]$和$v[i]$代表物品的重量和价值。 输出: 将计算结果输出到文件,包括最优价值和选取方案包括2行,第一行一个整数,表示计算结果,第二行包括一组序列,表示选取方案,按照$T={1,0,1,1}$,矩阵形式表示。要求使用分支限界法求解。
测试说明:
测试输入:
10 342 158 254 94 98 157 128 125 616 1416 9
预期输出:
85
#include <iostream>
using namespace std;
int maxSize=0;
/********** Begin **********/
void backtrack(int * weights, int * values, int sum, int value, int totalCapacity, int index, int num){
if(value >maxSize){
maxSize = value;
}
if (index>=num) {
return;
}
for (int i = 0; i <= 1; i++) {
if(sum + weights[index]*i <= totalCapacity){
backtrack(weights, values, sum + weights[index] * i, value + values[index] * i, totalCapacity, index + 1, num);
}
}
}
/********** End **********/
int main() {
/********** Begin **********/
int n;
int capacity;
cin >> n;
cin >> capacity;
int* weights = new int[n];
int* values = new int[n];
for (int i = 0; i < n; i++) {
cin >> weights[i];
cin >> values[i];
}
backtrack(weights, values, 0, 0, capacity, 0, n);
cout << maxSize << endl;
delete[] weights;
delete[] values;
/********** Begin **********/
return 0;
}
第2关:旅行商问题
任务描述:
本关任务:旅行商问题。
相关知识:
为了完成本关任务,你需要掌握:分支限界法。
问题描述:
某售货员要到若干城市去推销商品,已知各城市之间的路程,他要选定一条从驻地出发,经过每个城市一遍,最后回到住地的路线,使总的路程最短。
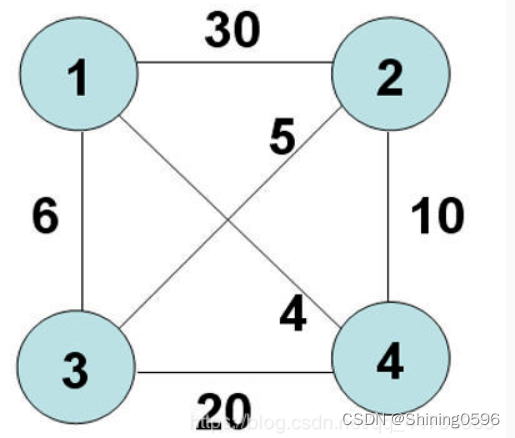
结果为: 1 3 2 4 1
问题分析:
解旅行售货员问题的优先队列式分支限界法用优先队列存储活结点表 活结点m在优先队列中的优先级定义为:活结点m对应的子树费用下界lcost。 lcost=cc+rcost,其中,cc为当前结点费用,rcost为当前顶点最小出边费用加上剩余所有顶点的最小出边费用和。 优先队列中优先级最大的活结点成为下一个扩展结点。 排列树中叶结点所相应的载重量与其优先级(下界值)相同,即:叶结点所相应的回路的费用(bestc)等于子树费用下界lcost的值。 与子集树的讨论相似,实现对排列树搜索的优先队列式分支限界法也可以有两种不同的实现方式:(旅行售货员问题采用第一种实现方式。)
- 用优先队列来存储活结点。优先队列中
每个活结点都存储从根到该活结点的相应路径。 - 用优先队列来存储活结点,并同时存储
当前已构造出的部分排列树。优先队列中的活结点不必存储从根到该活结点的相应路径,该路径必要时从存储的部分排列树中获得。


编程要求:
根据提示,在右侧编辑器补充代码,计算并输出数组的平均值和最大值。
测试说明:
输入数据: 第一行,有n个城市。 后面n行n列,代表n个城市直接的距离。没联系用-1代替。 输出数据: 一行。最优值,最优解的走法 平台会对你编写的代码进行测试:
平台会对你编写的代码进行测试:
测试输入:
4-1 30 6 430 -1 5 106 5 -1 204 10 20 -1
预期输出:
最优值为:25最优解为:1423
#include <iostream>
#define NO_PATH -1 //没有通路
#define MAX_WEIGHT 4000
using namespace std;
/********** Begin **********/
// 函数,全局变量,结构体等
int N; //城市数目
int City_Graph[100][100]; //保存图信息
int x[100]; //x[i]保存第i步遍历的城市
int isIn[100]; //保存 城市i是否已经加入路径
int bestw; //最优路径总权值
int cw; //当前路径总权值
int bestx[100]; //最优路径
void Travel_Backtrack(int t){ //递归法
int i,j;
if(t>N){ //走完了,输出结果
if(cw < bestw){ //判断当前路径是否是更优解
for (i=1;i<=N;i++){
bestx[i] = x[i];
}
bestw = cw+City_Graph[x[N]][1];
}
return;
}
else{
for(j=1;j<=N;j++){ //找到第t步能走的城市
if(City_Graph[x[t-1]][j] != NO_PATH && !isIn[j]){ //能到而且没有加入到路径中
isIn[j] = 1;
x[t] = j;
cw += City_Graph[x[t-1]][j];
Travel_Backtrack(t+1);
isIn[j] = 0;
x[t] = 0;
cw -= City_Graph[x[t-1]][j];
}
}
}
}
/********** End **********/
int main(){
/********** Begin **********/
int i;
cin>>N;
for(int i=1;i<=N;i++){
for(int j=1;j<=N;j++){
cin>>City_Graph[i][j];
}
}
//测试递归法
for (i=1;i<=N;i++){
x[i] = 0; //表示第i步还没有解
bestx[i] = 0; //还没有最优解
isIn[i] = 0; //表示第i个城市还没有加入到路径中
}
x[1] = 1; //第一步 走城市1
isIn[1] = 1; //第一个城市 加入路径
bestw = MAX_WEIGHT;
cw = 0;
Travel_Backtrack(2); //从第二步开始选择城市
cout<<"最优值为:"<<bestw;
cout<<"最优解为:";
for(i=1;i<=N;i++){
cout<<bestx[i];
}
cout<<endl;
/********** End **********/
return 0;
}