算法套路十七——买卖股票问题:状态机 DP
状态机DP是一种将动态规划方法应用于有限状态机(Finite State Machine)的问题求解方法。
状态机DP(State Machine DP)是一种动态规划的思想,它通常用于解决一些具有状态转移的问题。在状态机DP中,我们将问题抽象成一个状态机,其中每个状态表示问题的一个子问题,每个状态之间存在状态转移,表示从一个子问题转移到另一个子问题的过程。状态机DP方法也适用于涉及多个子问题之间存在依赖关系的问题,例如字符串匹配、序列比较等。
买卖股票问题是一种典型的状态机 DP问题,设"未持有股票"和"持有股票"两个状态,每个节点表示某一状态下的最大收益,相邻节点之间的边表示在当前状态下进行一次交易得到的收益。

算法示例一:LeetCode122. 买卖股票的最佳时机 II
给你一个整数数组 prices ,其中 prices[i] 表示某支股票第 i 天的价格。
在每一天,你可以决定是否购买和/或出售股票。你在任何时候 最多 只能持有 一股 股票。你也可以先购买,然后在 同一天 出售。
返回 你能获得的 最大 利润 。
法一:递归+记忆化搜索
- 递归函数:
dfs(i, hold)表示到第i日,手上是否拿着股票所得到的最大收益。hold为true则表示有股票,为false则表示没有股票 - 转移方程:
- 如果第
i
i
i天持有股票,那么当前最大收益由两种可能转移而来:
- 在第 i − 1 i - 1 i−1天持有股票的情况下并选择不卖出:此时收益就是 d f s ( i − 1 , T r u e ) dfs(i - 1, True) dfs(i−1,True);
- 在第 i − 1 i - 1 i−1天不持有股票的情况下并选择买入:此时收益就是 d f s ( i − 1 , F a l s e ) − p r i c e s [ i ] dfs(i - 1, False) - prices[i] dfs(i−1,False)−prices[i],当前利润减去当天价格。
- 取两者最大值作为转移结果。
- 如果第
i
i
i天未持有股票,那么当前最大收益由两种可能转移而来:
- 在第 i − 1 i - 1 i−1天未持有股票的情况下并选择不购买:此时收益就是 d f s ( i − 1 , F a l s e ) dfs(i - 1, False) dfs(i−1,False);
- 在第 i − 1 i - 1 i−1天持有股票的情况下并选择卖出:此时收益就是 d f s ( i − 1 , T r u e ) + p r i c e s [ i ] dfs(i - 1, True) + prices[i] dfs(i−1,True)+prices[i],因为当前不具有股票而获得了可用资金。
- 取两者最大值作为转移结果。

- 如果第
i
i
i天持有股票,那么当前最大收益由两种可能转移而来:
- 边界值:当遍历完所有即i<0时,如果持有股票,返回负无穷(代表不合法状态);否则返回0
- 返回值:dfs(n - 1, False)
class Solution:
def maxProfit(self, prices: List[int]) -> int:
n = len(prices)
@cache # 使用缓存装饰器,加速递归函数计算
# i 表示当前考虑到的股票价格下标,hold 表示当前是否持有股票
def dfs(i: int, hold: bool) -> int:
if i < 0: # 如果已经遍历完所有股票价格
return -inf if hold else 0 # 如果持有股票,返回负无穷(代表不合法状态);否则返回零利润。
# 如果当前已经持有一支股票
if hold:
#卖或不卖
return max(dfs(i - 1, True), dfs(i - 1, False) - prices[i])
#买或不买
return max(dfs(i - 1, False), dfs(i - 1, True) + prices[i])
return dfs(n - 1, False)
法二:二维dp数组动态规划
直接利用上述递归+记忆化搜索代码转换为动态规划
dp[i][0]表示第i天结束后手里没有股票的最大收益,dp[i][1]表示第i天结束后手里持有一支股票的最大收益,最后返回dp[n][0],表示在最后一天卖出所有手头的股票后得到的最大收益
class Solution:
def maxProfit(self, prices: List[int]) -> int:
n = len(prices)
dp = [[0] * 2 for _ in range(n + 1)]
dp[0][1]=-inf
for i, price in enumerate(prices):
#当前没有股票,只能不买或卖
dp[i+1][0]=max(dp[i][0],dp[i][1]+price)
#当前有股票,只能买或不卖
dp[i+1][1]=max(dp[i][0]-price,dp[i][1])
return dp[n][0]
算法练习一:LeetCode714. 买卖股票的最佳时机含手续费
给定一个整数数组 prices,其中 prices[i]表示第 i 天的股票价格 ;整数 fee 代表了交易股票的手续费用。
你可以无限次地完成交易,但是你每笔交易都需要付手续费。如果你已经购买了一个股票,在卖出它之前你就不能再继续购买股票了。
返回获得利润的最大值。
注意:这里的一笔交易指买入持有并卖出股票的整个过程,每笔交易你只需要为支付一次手续费。
与示例一样的思路,只是需要在购买时不仅减去股票价格,并减去手续费
func maxProfit(prices []int, fee int) int {
n := len(prices)
dp := make([][]int, n+1)
for i := range dp {
dp[i] = make([]int, 2)
}
dp[0][1] = -math.MaxInt32
for i, price := range prices {
//不买或卖
dp[i+1][0] = max(dp[i][0], dp[i][1]+price)
//买并支付小费
dp[i+1][1] = max(dp[i][0]-price-fee, dp[i][1])
}
return dp[n][0]
}
func max(x, y int) int {if x > y {return x};return y}
算法练习二:LeetCode309. 最佳买卖股票时机含冷冻期
给定一个整数数组prices,其中第 prices[i] 表示第 i 天的股票价格 。设计一个算法计算出最大利润。在满足以下约束条件下,你可以尽可能地完成更多的交易(多次买卖一支股票):
卖出股票后,你无法在第二天买入股票 (即冷冻期为 1 天)。
注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
本题与示例唯一的差距在于多了冷冻期,而这也只会影响买股票这一种情况,由于冷冻期,所以在计算买股票这种情况时,只能用2天前且手上没有股票的最大利润来计算,且第一天结束时不存在前一天买入的情况,因此我们需要对第一天单独处理。
func maxProfit(prices []int) int {
n := len(prices)
dp := make([][]int, n+1)
for i := range dp {
dp[i] = make([]int, 2)
}
//-math.MaxInt32表示不符合现实
dp[0][1] = -math.MaxInt32
for i, price := range prices {
//当前没有股票,只能不买或卖
dp[i+1][0] = max(dp[i][0], dp[i][1]+price)
//当前有股票,只能买或不卖
if i>0{
//i>0时,对于买的情况,由于冷冻期所以只能用dp[i-1][0]即2天前且手上没有股票的最大利润
dp[i+1][1] = max(dp[i-1][0]-price, dp[i][1])
}else {
//i=0即第一天想要有股票只能买
dp[i+1][1] =-price
}
}
return dp[n][0]
}
func max(x, y int) int {if x > y {return x};return y}
算法练习三:LeetCode123. 买卖股票的最佳时机 III
给定一个数组,它的第 i 个元素是一支给定的股票在第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你最多可以完成 两笔 交易。
注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
递归+记忆化搜索
首先思考递归+记忆化搜索来开拓思路,易知可以在递归中添加一个参数j,来记录当前遍历次数,代码如下所示
class Solution:
def maxProfit(self, prices: List[int]) -> int:
n = len(prices)
# 使用cache装饰器来实现记忆化搜索
@cache
def dfs(i: int, j: int, hold: bool) -> int:
# 如果j小于0,表示交易次数已经用完,返回负无穷
if j < 0:
return -inf
# 如果i小于0,表示已经到达第0天,如果持有股票,返回负无穷,否则返回0
if i < 0:
return -inf if hold else 0
if hold:
return max(dfs(i - 1, j, True), dfs(i - 1, j - 1, False) - prices[i])
else:
return max(dfs(i - 1, j, False), dfs(i - 1, j, True) + prices[i])
return dfs(n - 1, 2, False)
动态规划
根据以上递归过程转换为动态规划,递归函数添加了一个参数,所以我们在动态数组dp中添加一维交易次数,其中dp[i][j][0]表示第i天,最多进行j次交易,且当前不持有股票的最大收益,dp[i][j][1]表示第i天,最多进行j次交易,且当前持有股票的最大收益。
不过需要注意,只有买时才算一次新的交易次数,而卖不算一次新的交易
func maxProfit(prices []int) int {
n := len(prices)
dp := make([][][2]int, n+1)
for i:=range dp{
dp[i]=make([][2]int,3)
for j:=0;j<3;j++{
dp[i][j][1] = math.MinInt32/2
}
}
for i:=0;i<n;i++{
for j:=0;j<2;j++{
//不买或卖
dp[i+1][j+1][0]=max(dp[i][j+1][0],dp[i][j+1][1]+prices[i])
//不卖或买,买即增加一次交易
dp[i+1][j+1][1]=max(dp[i][j+1][1],dp[i][j][0]-prices[i])
}
}
return dp[n][2][0]
}
func max(x, y int) int {if x > y {return x};return y}
算法练习四:LeetCode188. 买卖股票的最佳时机 IV
给定一个整数数组 prices ,它的第 i 个元素 prices[i] 是一支给定的股票在第 i 天的价格,和一个整型 k 。
设计一个算法来计算你所能获取的最大利润。你最多可以完成 k 笔交易。也就是说,你最多可以买 k 次,卖 k 次。
注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
直接采用上题的思路,将j的范围由0-2修改到0-k即可
func maxProfit(k int, prices []int) int {
n := len(prices)
dp := make([][][2]int, n+1)
for i:=range dp{
dp[i]=make([][2]int,k+1)
for j:=0;j<k+1;j++{
dp[i][j][1] = math.MinInt32/2
}
}
for i:=0;i<n;i++{
for j:=0;j<k;j++{
//不买或卖
dp[i+1][j+1][0]=max(dp[i][j+1][0],dp[i][j+1][1]+prices[i])
//不卖或买,买即增加一次交易
dp[i+1][j+1][1]=max(dp[i][j+1][1],dp[i][j][0]-prices[i])
}
}
return dp[n][k][0]
}
func max(x, y int) int {if x > y {return x};return y}
算法练习五:LeetCode1911. 最大子序列交替和
一个下标从 0 开始的数组的 交替和 定义为 偶数 下标处元素之 和 减去 奇数 下标处元素之 和 。
比方说,数组 [4,2,5,3] 的交替和为 (4 + 5) - (2 + 3) = 4 。
给你一个数组 nums ,请你返回 nums 中任意子序列的 最大交替和 (子序列的下标 重新 从 0 开始编号)。
一个数组的 子序列 是从原数组中删除一些元素后(也可能一个也不删除)剩余元素不改变顺序组成的数组。比方说,[2,7,4] 是 [4,2,3,7,2,1,4] 的一个子序列(加粗元素),但是 [2,4,2] 不是。
类比买卖股票,区别在于本题刚开始就已经0元买进了股票,故初始化数组dp[0][1] =0,dp[0][0] =math.MinInt64 / 2,其余则和示例思路一样
func maxAlternatingSum(nums []int) int64 {
//类比买卖股票,即第一次0元买进,之后卖出
n := len(nums)
dp := make([][]int, n+1)
for i := range dp {
dp[i] = make([]int, 2)
}
//负无穷表示不符合题意,/2防止越界
dp[0][0] =math.MinInt64 / 2
//开始0元买进了股票
dp[0][1] =0
for i, num := range nums {
dp[i+1][0] = max(dp[i][0], dp[i][1]+num)
dp[i+1][1] = max(dp[i][0]-num, dp[i][1])
}
return int64(dp[n][0])
}
func max(x, y int) int {if x > y {return x};return y}

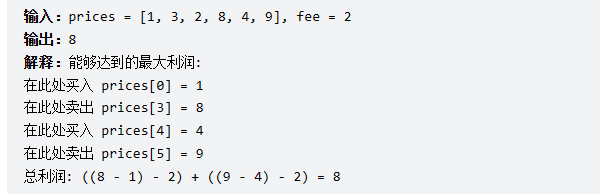








![vector容器 [上]](https://img-blog.csdnimg.cn/b65b7ee01de141059a6716fcc9f4cbfd.png)