第十四章、数据结构及算法应用
1、分治法
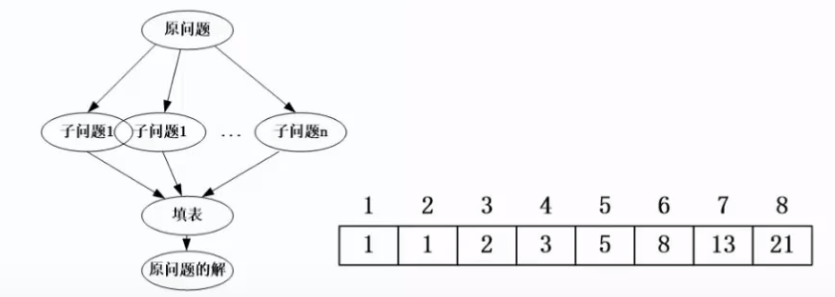
对于一个规模为n的问题,若该问题可以容易地解决(比如说规模n较小)则直接解决;否则将其分解为k个规模较小的子问题,这些子问题互相独立且与原问题形式相同,递归地解这些子问题,然后将各子问题的解合并得到原问题的解
- 该问题的规模缩小到一定的程度就可以容易地解决
- 该问题可以分解为若干个规模较小的相同问题
- 利用该问题分解出的子问题的解可以合并为该问题的解
- 该问题所分解出的各个子问题是相互独立的
1.1、递归技术
递归,就是在运行的过程中调用自己
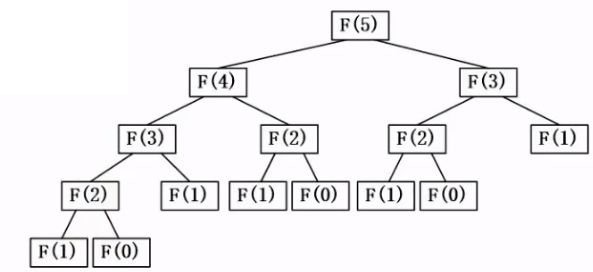
斐波那契数列
int F(int n)
{
if(n=0) return 1;
if(n=1) return 1;
if(n>1) return F(n-1)+F(n-2);
}
1.2、二分查找
二分查找也称折半查找(Binary Search),它是一种效率较高的查找方法。但是,折半查找要求线性表必须采用顺序存储结构,而且表中元素按关键字有序排列
function Binary_Search(L,a,b,x){
if(a>b) return -1;
else{
m=(a+b)/2;
if(x==L[m])return m;
else if(x>L[m])
return(Binary_Search(L,m+1,b,x));
else
return(Binary_Search(L,a,m-1,x));
}
}
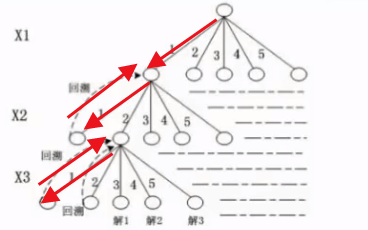
2、回溯法
回溯法是一种选优搜索法,按选优条件向前搜索,以达到目标。但当搜索到某一步时,发现原先选择并不优或达不到目标,就退回一步重新选择。这种走不通就退回再走的技术就是回溯法。


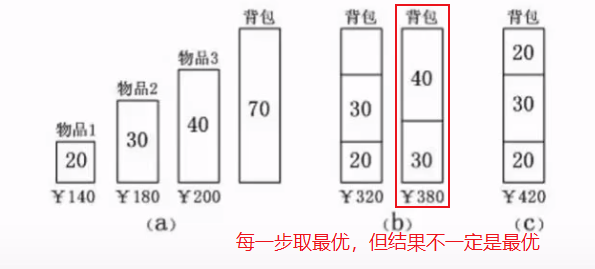
3、贪心法
总是做出在当前来说是最好的选择,而并不从整体上加以考虑,它所做的每步选择只是当前步骤的局部最优选择,但从整体来说不一定是最优的选择。由于它不必为了寻找最优解而穷尽所有可能解,因此其耗费时间少,一般可以快速得到满意的解,但得不到最优解。
4、动态规划法
在求解问题中,对于每一步决策,列出各种可能的局部解,再依据某种判定条件,舍弃那些肯定不能得到最优解的局部解,在每一步都经过筛选,以每一步都是最优解来保证全局是最优解。