1. 正则化的思想

• 如果特征的参数值更小，那么对模型有影响的特征就越少，模型就越简单，因此就不太容易过拟合
  
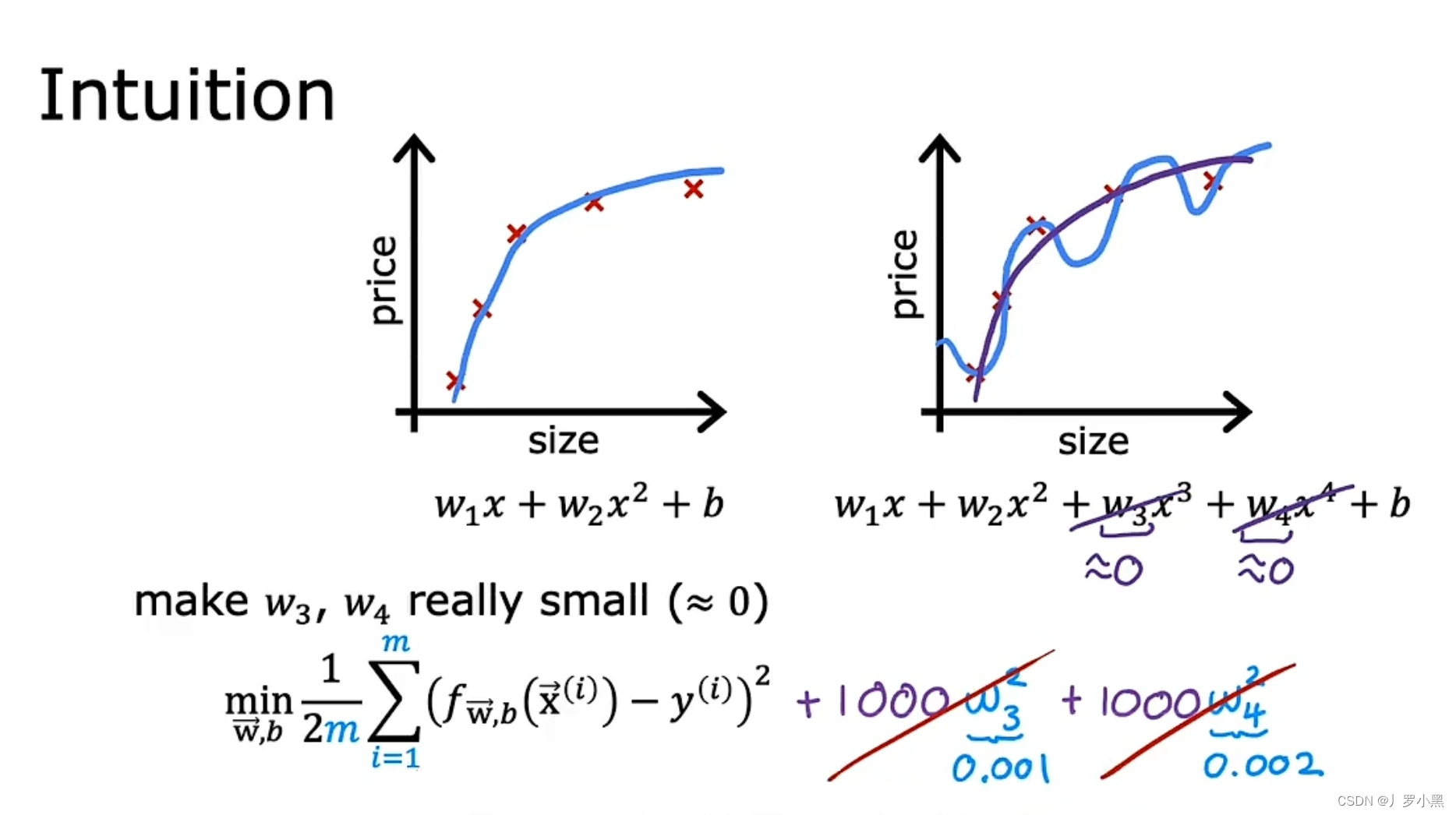
• 如上图所示，成本函数中有W₃和W₄，且他们的系数很大，要想让该成本函数达到最小值，就得使W₃和W₄接近0，从而消除它们对成本函数的影响，最后我们就得出一个接近二次函数（左边图片）的成本函数

2. 正则化的一般形式

• 通常，一个模型有很多特征，我们不知道哪个特征的参数重要，哪个特征的参数我们需要缩小或惩罚。所以，我们一般是缩小或惩罚所有特征的参数。
• 一般来说，我们可以给成本函数加上，Wj和b的正则项，其中b的正则项可加可不加
• λ为正则参数，且λ > 0
• 给正则参数λ 除以 2m ，即与第一项采用相同缩放1/2m，可以当训练集发生改变时，原λ可能可以不变
  

3. 正则化的最终形式
   

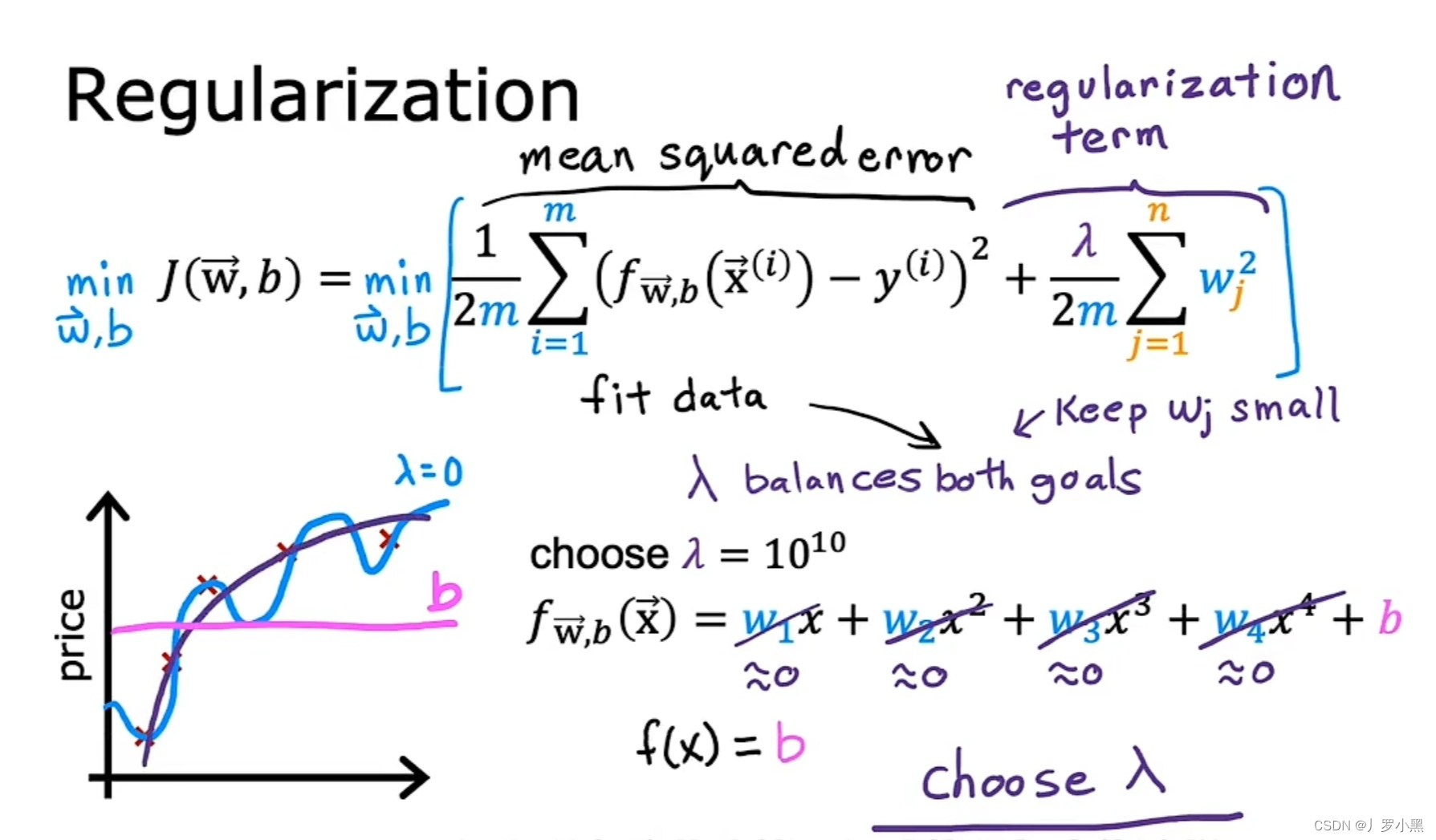
• 正则化后的成本函数由平均误差项和正则化项组成，而最小化成本函数即最小化第一项（使预测值更好的拟合训练数据集），和最小化第二项（使特征的参数保持较小的值，防止过拟合）
• λ则用来在最小化这两个项之间获得平衡，不能过大，也不能过小
• 当λ取0时，正则化项为0，即它并没有在最小化成本函数的过程中发挥作用，会导致函数过于复杂，模型过拟合
• 当λ取10¹⁰时，为了最小化成本函数，就要最小化正则化项，那么Wj必须非常接近0，即W的所有值都必须非常接近0，会导致函数平行于x轴，模型欠拟合

4. 线性回归的梯度下降算法的正则化

• 因为我们没有对b进行正则化，所以更新b的时候不需要进行缩小操作，与不正则化保持相同
  
• α和λ都是非常小的正数，比如分别是0.01和1，那么它们的乘积再除以m就是一个很小很小的正数，Wj乘以 ( 1 - 这个正数 ) 就相当于缩小Wj一点点
• 正则化的工作原理：在每次迭代中都缩小Wj一点点，即乘以一个稍小于1的数
  
• 导数项的计算过程中，对W的正则化项求Wj偏导时，把W₁、W₂等看成常数，就可去除求和符号

5. 逻辑回归的梯度下降算法的正则化
   

• 逻辑回归的成本函数与线性回归的成本函数相同，都是在结尾加上Wj的正则化项
• 当我们采用正则化时，即使我们的模型有很多复杂的高阶特征，仍然可以得到一个合理的决策边界，并可以很好的预测从未出现的新示例
  
• 逻辑回归的梯度下降算法的正则化与线性回归的梯度下降算法的正则化，看起来相同，但是他们的f(x)函数不同
• 逻辑回归也没有对b进行正则化，所以更新b时也不需要进行缩小操作