多维时序 | MATLAB实现CNN-BiGRU卷积神经网络结合双向门控循环单元多变量时间序列预测

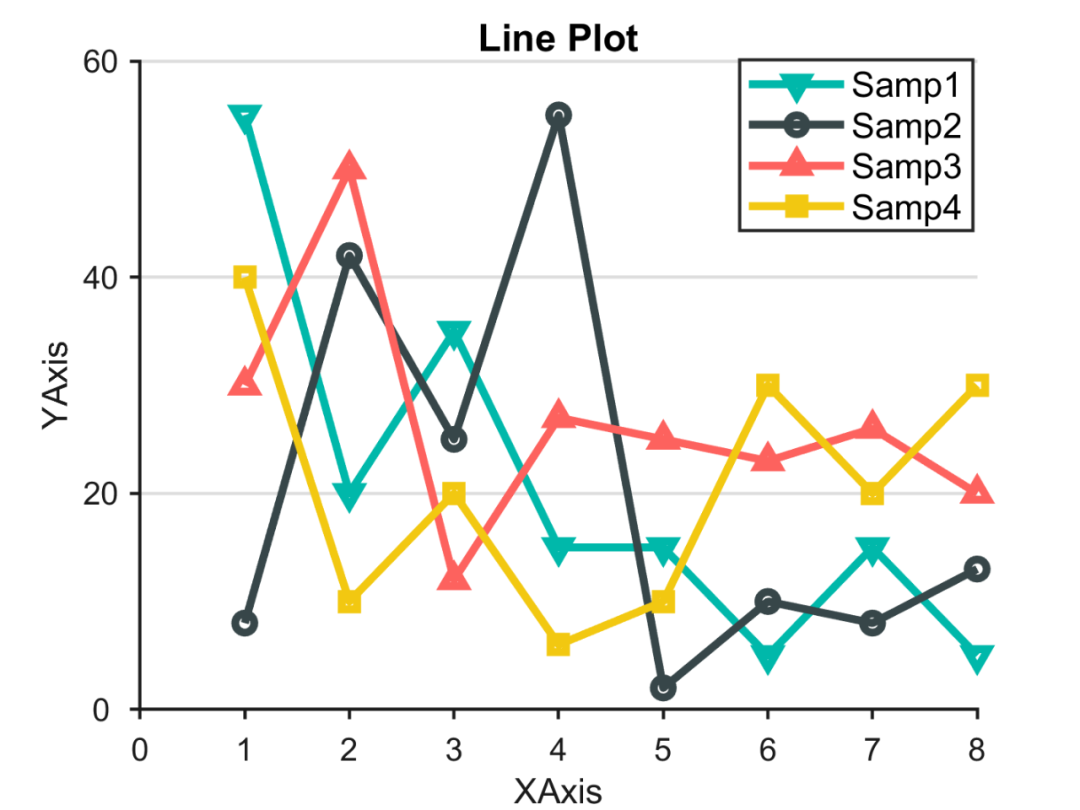
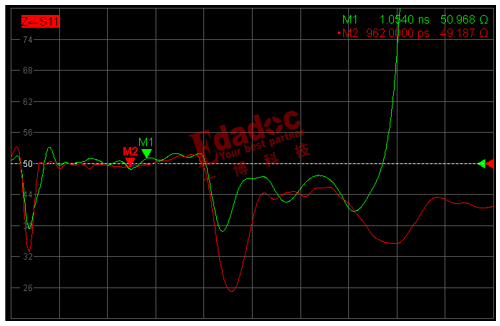
预测结果

基本介绍

多维时序 | MATLAB实现CNN-BiGRU卷积神经网络结合双向门控循环单元多变量时间序列预测
1.Matlab实现CNN-BiGRU卷积神经网络结合双向门控循环单元多变量时间序列预测；
2.运行环境为Matlab2020b；
3.输入多个特征，输出单个变量，考虑历史特征的影响，多变量时间序列预测；
4.data为数据集，MainCNN_BiGRUNTS.m为主程序，运行即可,所有文件放在一个文件夹；
5.命令窗口输出R2、MSE、MAE、MAPE和MBE多指标评价；

模型特点

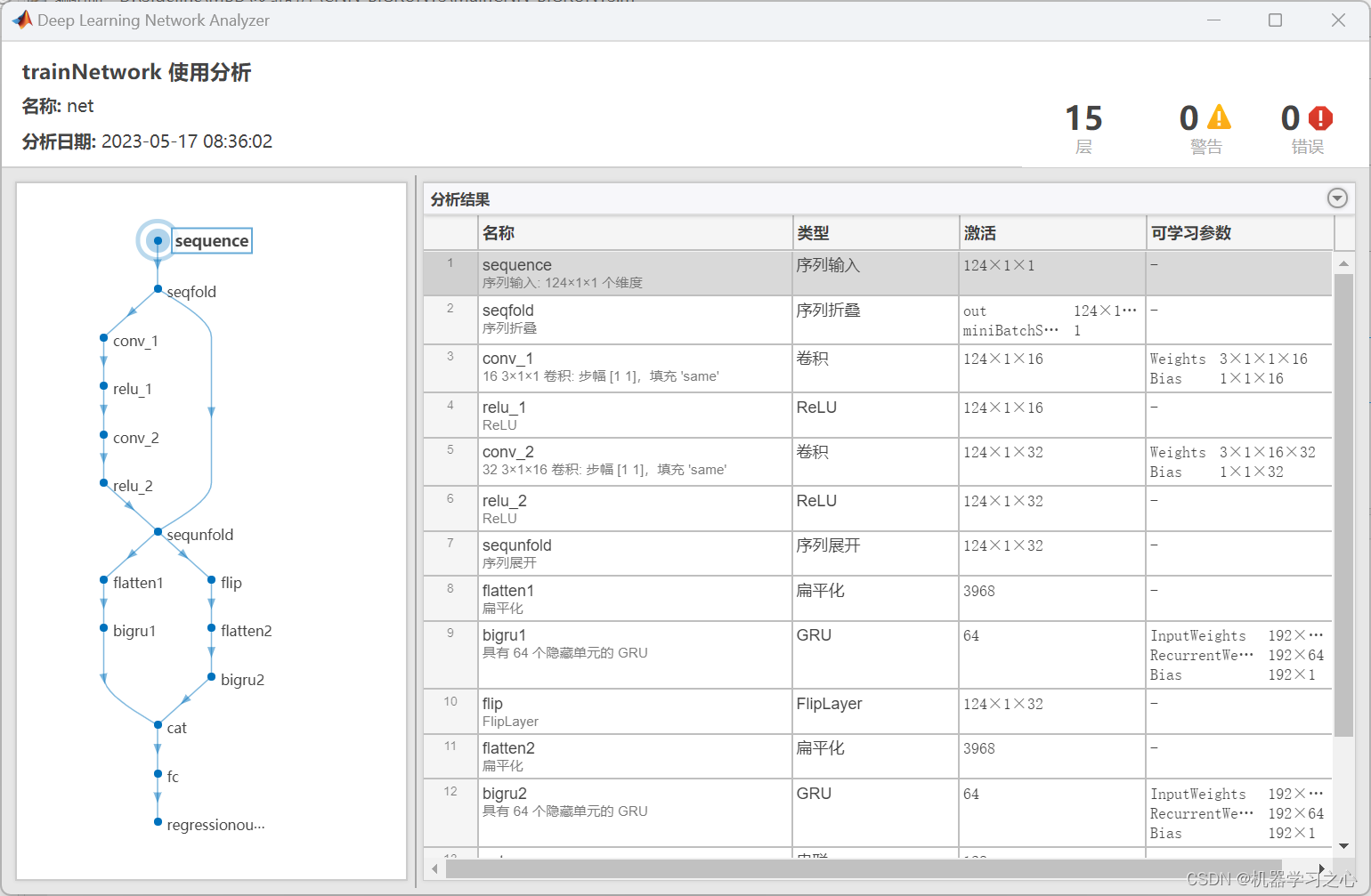
CNN-BiGRU模型结合了卷积神经网络（CNN）和双向门控循环单元（BiGRU），主要用于对多变量时间序列数据进行预测。下面总结一下该模型的主要特点：

• 建模多个变量之间的相关性：CNN-BiGRU模型能够对多个变量之间的相关性进行建模，从而提高预测的准确性和稳定性。
• 自适应特征选择：该模型能够自适应地选择重要的特征，从而减少噪声和冗余信息对预测结果的影响。
• 序列建模能力：双向门控循环单元能够学习序列中的长期依赖关系，从而更好地捕捉时间序列中的动态变化。
• 鲁棒性：CNN-BiGRU模型能够处理缺失值和异常值，并且对输入数据进行了归一化和标准化，从而提高了模型的鲁棒性和泛化能力。
• 可扩展性：该模型能够灵活地调整网络结构和超参数，以适应不同的数据集和任务，并且可以与其他深度学习模型进行集成和组合，以进一步提高预测效果。

需要注意的是，CNN-BiGRU模型也存在一些限制和挑战，例如训练时间较长、模型结构较为复杂、需要大量的数据和计算资源等等。在实际应用中，需要根据具体情况进行模型的优化和改进，以提高预测效果和效率。

程序设计

• 完整源码和数据私信博主获取。

% 定义CNN层参数
filterSize = [3 3];
numFilters = 32;
poolSize = [2 2];

% 定义BiGRU层参数
numHiddenUnits = 64;
outputMode = 'last';

% 定义全连接层参数
numClasses = 1;

% 定义网络结构
layers = [
    sequenceInputLayer(numFeatures)
    convolution2dLayer(filterSize, numFilters, 'Padding', 1)
    reluLayer
    maxPooling2dLayer(poolSize, 'Stride', 2)
    sequenceFoldingLayer
    gruLayer(numHiddenUnits, 'OutputMode', outputMode, 'Bidirectional', true)
    fullyConnectedLayer(numClasses)
    regressionLayer];

% 定义训练选项
options = trainingOptions('adam', ...
    'MaxEpochs', 20, ...
    'MiniBatchSize', 32, ...
    'ValidationData', {XValidation, YValidation}, ...
    'ValidationFrequency', 10, ...
    'Verbose', false);

% 训练模型
net = trainNetwork(XTrain, YTrain, layers, options);

% 预测结果
YPred = predict(net, XTest);

学习总结

CNN-BiGRU模型结合了卷积神经网络（CNN）和双向门控循环单元（BiGRU），主要用于对多变量时间序列数据进行预测。该模型的主要特点是能够对多个变量之间的相关性进行建模，并且能够自适应地选择重要的特征。
具体来说，该模型首先使用卷积神经网络对多个变量的时间序列数据进行特征提取，然后将这些特征输入到双向门控循环单元中进行序列建模。双向门控循环单元能够学习序列中的长期依赖关系，并且可以自适应地选择哪些特征对预测结果最有用。最后，该模型使用全连接层对输出进行处理，得到最终的预测结果。
使用该模型进行多变量时间序列预测，需要准备好相应的数据集，并对模型进行训练和调参。在实际应用中，还需要根据具体情况进行模型的优化和改进，以提高预测效果。

参考资料

[1] https://blog.csdn.net/kjm13182345320/article/details/127515229?spm=1001.2014.3001.5502
[2] https://blog.csdn.net/kjm13182345320/article/details/127993418?spm=1001.2014.3001.5502