第一篇我们系统的介绍了傅里叶级数、傅里叶变换、离散傅里叶变换。本篇介绍快速傅里叶变换,并说说傅里叶变换在二维图像上是如何应用的。
首先我们快速的回顾一下第一篇内容,伟大的法国数学家、物理学家——让·巴普蒂斯·约瑟夫·傅里叶,发现了周期函数都可以写成N个正余弦乘以一个系数的累加和,他称这样的变换方法为傅里叶级数展开;随后有更多个科学家在这基础上不断发展,把傅里叶级数和欧拉公式相结合,提出连续的傅里叶变换;再结合数字化采样提出离散傅里叶变换。但是以当时的计算机性能,离散傅里叶的计算量还是挺巨大的,运算时间太长。在(美苏冷战)历史背景下,人们需要想办法提升效率。就此历史背景,在1965年由J.W.库利和T.W.图基提出的一种快速傅里叶计算方法,能使计算机计算离散傅里叶变换所需要的乘法次数大为减少,特别是在变换的抽样点数N递增越多,快速傅里叶算法计算量的节省就尤为越显著。
快速离散傅里叶计算
快速傅里叶并不是什么新概念理论,它只是利用了数学之美,提升了离散傅里叶变换的计算效率。接下来我们简单了解 快速傅里叶的具体思路。
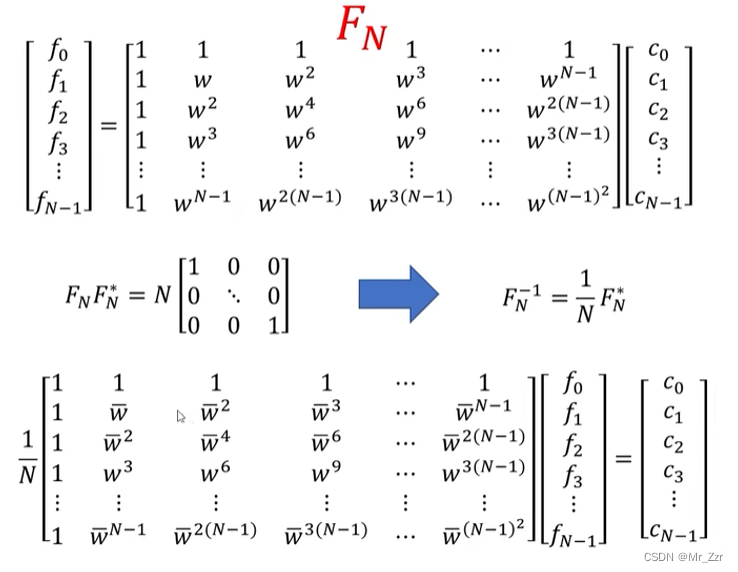
首先我们回顾一下傅里叶矩阵、离散傅里叶变换的公式来源。那么快速傅里叶是快速的去计算这个矩阵乘法的一个数学算法。但并不是任何一个随机矩阵都能快速计算的,这个就需要线性代数去讨论处理了。按照矩阵乘法的公式,傅里叶矩阵左乘采样向量的过程中,一个元素就要运行N次乘法+N-1次加法,N个元素那就是需要N²次乘法运算。

在推算快速傅里叶变换前,我们简单介绍一下行列向量乘法的一个特性,简单理解其实就是行列向量当中的元素对位交换,运算结果不变。这个特性在推导快速傅里叶运算中要用到。
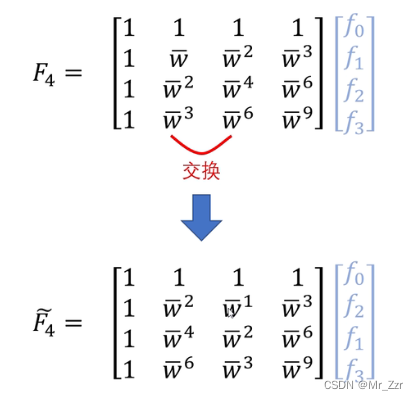
如上图所示,以4维度的离散傅里叶矩阵为例,运用上面提到的行列交换的性质,如果是8维度的,那 F~ 就变成[w0',w2',w4',w6',w1',w3',w5',w7']如此类推。那为什么要这样交换元素排列,交换后有什么特殊性质?
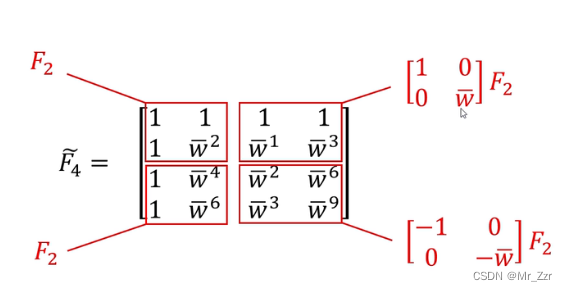
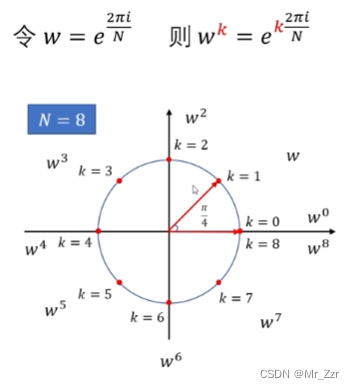
集合离散傅里叶变换当中提及到的欧拉圆所示(注意例子是4个采样点为一个周期,所以对应上图的欧拉圆应该是N=4)w0=w4=1,w2=w6,如此类推以4为采样周期的交换后傅里叶矩阵F~可分为如上左图所示的4个分块。


从例子再结合代数表达式,可以推导出一个交换后的傅里叶矩阵的一般情况,并总结出一个加速运算的流程,。那么从上面的分析流程发现,对于快速傅里叶计算,对离散采样个数N是有要求的,N最好是2的倍数,为什么说最好是2的倍数呢。因为从实际例子上说明,四维的离散傅里叶矩阵F可以分为了4个二维矩阵,那么九维的离散傅里叶矩阵也是可以分成9个三维的矩阵。所以实际上N只要满足N=n*n就可以了。
但是理论上或者实际上,N都会选2的k次幂呢?主要是因为2的k次幂可以一直的往下拆分,拆分到二维矩阵。而且现实情况N是可以自主给定的,这是测试过程的采样个数,选取2的k次幂自然而然的也没什么难度。所以说2的k次幂就成为快速傅里叶默认的条件了。

那么我们继续上面的拆解流程,我们把采样变换后的列向量再划分为两部分(even偶odd奇),最终离散傅里叶逆变换求解就有个快速求解公式。为什么这个化简就能加速离散傅里叶逆变换的求解?我们可以看看左边Fn·X的乘法运算次数是N*N次。而化简公式,先看右边部分F的N/2各自乘以X的奇偶部分,乘法运算次数是2*N/2*N/2次,再加上左边的矩阵也可以发现它里面的每个分块都是对角矩阵,也就是N次乘法。也就是说一次降维分解,运算数量级可以从 N² 次乘法变成 N² /4 + N次乘法。而且这只是一次降维分解节省的计算量,Fn/2·Xeven 这部分是不是可以递归继续降维拆分?
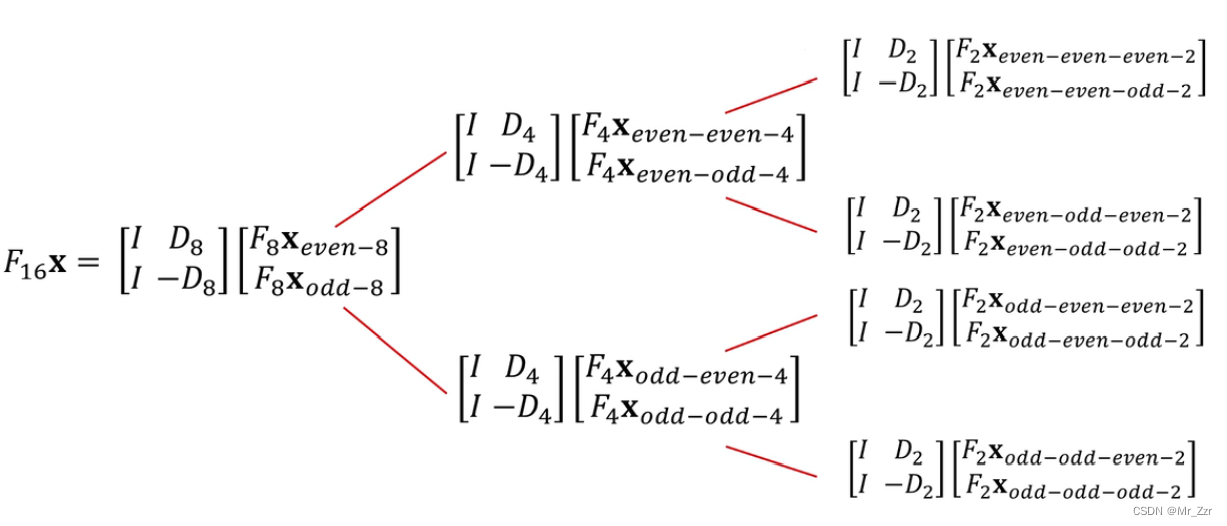
上图基本接近现代计算机数学运算库的计算逻辑,譬如要算16维的傅里叶矩阵,那么最后分解成四组2维的快速傅里叶,那么计算机先计算这四组最基础的2维快速傅里叶矩阵,然后自下而上的一步步的往上计算需要的结果。至此介绍完快速傅里叶变换的数学演变过程。
二维离散傅里叶变换
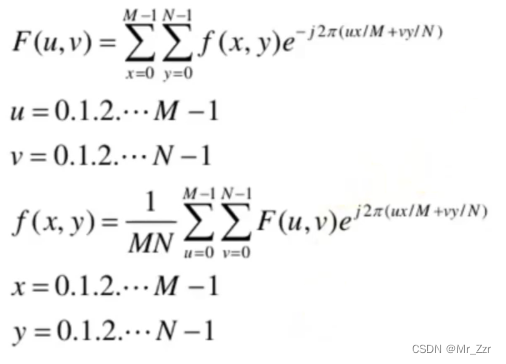
接下来介绍二维离散傅里叶变换,其实它是针对图像进行的。这里直接看二维离散傅里叶变换的公式。如果说忽略与y-v相关的所有项,其实x-u就是一个标准的一维连续傅里叶变换公式。在这里 f ( x , y )对应图像的某一个坐标。而u,v分别对应着x方向和y方向的频率分量。
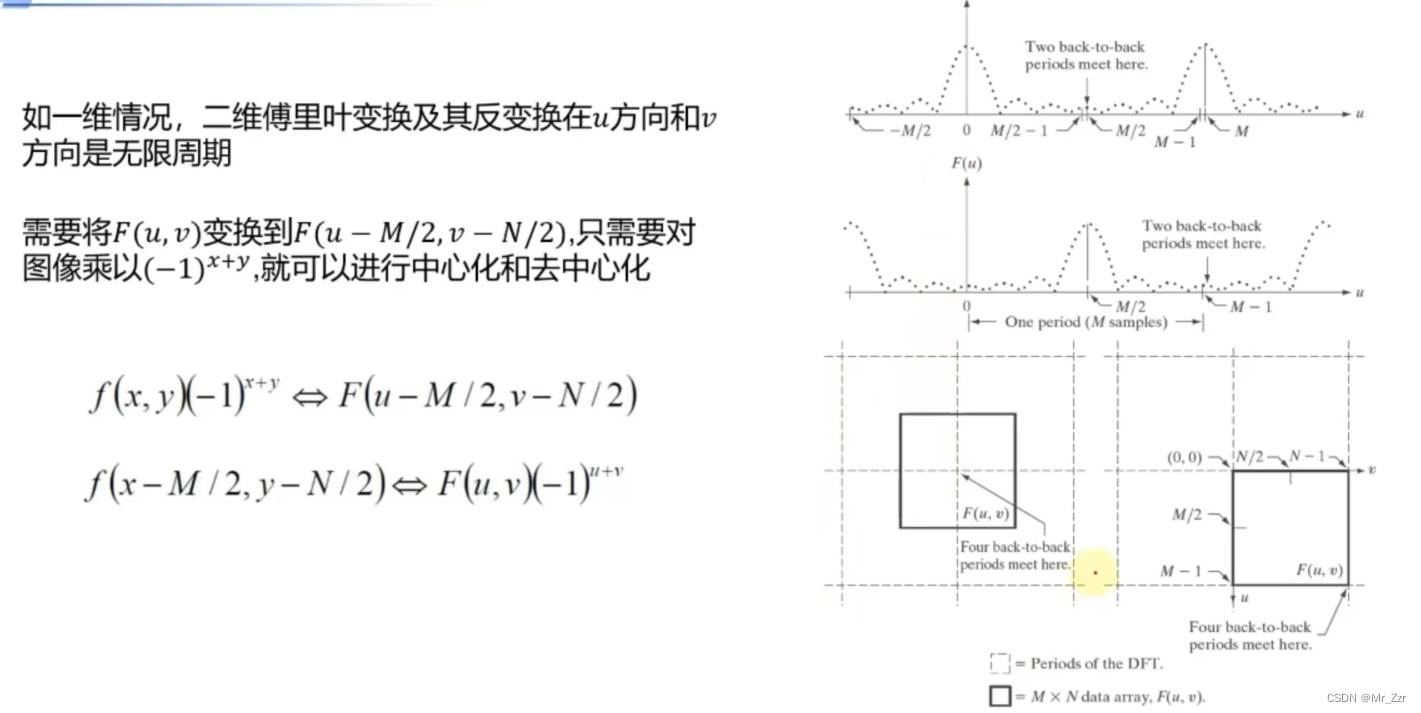
有一点需要注意的是,由于图像是离散信号,但是对应的频谱是连续周期的。这样子就会使得在一个周期内,图像频谱的低频部分在边缘四周,为了观测方便通常需要将它进行中心化。中心化操作的方法就是对原来的图像乘上-1的x+y次方,那么与之相对应的频谱就是中心化的。

频谱中心化作用是什么,如上所示一张傅里叶的画像进行二维傅里叶变换的频谱进行操作。
- 左上图示,去除四周高频部分,只保留低频频谱,可以看到对应的图像看着很模糊,内容细节丢失。
- 右上图示,去除中心低频部分,只保留高频频谱,可以看到对应的图像只看到一些噪点和边缘细节,对于它的颜色比较相同的部分已经滤除掉了。
以上就是二维傅里叶变换在图像处理当中的,频谱滤波的原理。