FPGA复位信号设计讨论

news2024/11/26 22:20:30

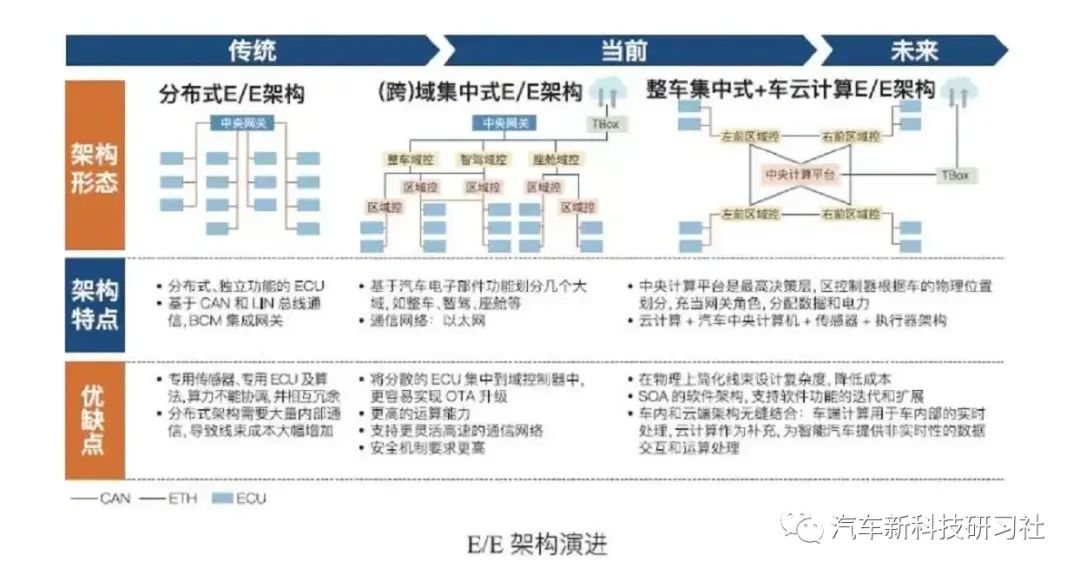
复位概述

复位作为电子系统中最常见的信号同时也是最重要的信号，它对工程师整体的设计表现有着极大的影响。复位信号可能深刻影响设计的性能表现，功耗，面积等等。对于一个优秀的系统设计，很难不把复位信号当成一个关键信号来设计。

同步的代码可能会综合出LUTs，Registers，SRLs，Block or LUT memory，DSP48 registers。对复位方式的不同选择以及对复位的使用不同会影响基本元件的选择。可能会引入更多或者更少的资源，影响整体设计的表现，功耗，甚至会导致系统运行异常。

什么时候什么地方使用复位？

对于很多新入门工程师来讲，很少会评估是否需要复位信号，绝大所数都是使用提供的模板，对所有的信号进行复位，尽管可能不是那么必要，如果是这样会增加资源，对复位时序也会产生影响，所以评估是否需要复位是很有必要的。

对赛灵思器件而言，厂家对FPGA提供了专用的全局复位（GSR）。这个信号在配置结束会把所有的时序元件都设置为一个初始的值。如果这个初始值没有被指定，大多数情况下都会被设置为0。每个器件都会在配置结束设置为一个定值，因此，有些上电时单一目的复位必要性不是很大。下面代码初始化registers和latches的指定初始值。

// Verilog代码
reg register1 = 1’b0; // specifying regsiter1 to start as a zero
reg register2 = 1’b1; // specifying register2 to start as a one
reg [3:0] register3 = 4’b1011; //specifying INIT value for 4-bit register

-- VHDL代码
signal reg1 : std_logic := '0'; -- specifying register1 to start as a zero
signal reg2 : std_logic := ‘1’; -- specifying register2 to start as a one
signal reg3 : std_logic_vector(3downto0):="1011"; -- specifying INIT value for 4-bit register

所以像之前所诉述，工程师应该仔细考虑和评估什么时候，什么地方需要复位。因为不必要的复位可能会导致诸多的问题。限制复位的使用可能具备的优势：

限制全局复位网络的扇出
减少复位路径的互联
简化复位路径的时序分析
提升整体设计的性能表现，面积，功耗等

功能性的仿真是可以容易区分复位是否需要，所以建议去评估每一个同步模块是否需要复位，尽量减少在未评估真实需要复位的情况下就引入复位。

同步复位异步复位

同步复位就是复位信号在时钟触发边沿才有效，简单讲敏感列表中没有复位信号，异步复位在复位信号被置位后即有效，简单说敏感列表中存在复位信号。如下面两段Verilog代码：

// 同步复位
module sync_resetFFstyle (
 outputreg q,
 input d, clk, rst_n);
always @(posedge clk)
 if (!rst_n)
     q <= 1'b0;
 else
     q <= d;
endmodule

// 异步复位
module async_resetFFstyle (
 outputreg q,
 input d, clk, rst_n);
 always @(posedge clk ornegedge rst_n)
 if (!rst_n)
     q <= 1'b0;
 else
     q <= d;
endmodule

同步复位相比较异步复位有以下的特点：

同步复位可以映射更多种类的资源单元
全局的异步复位会增加设计元件的布线复杂度（每个register都要连接复位信号）
如果需要提高电路的集成密度或者对电路进行调优布局，同步复位更加灵活
有些资源仅提供提供同步复位，如DSP48和RAM模块，如果使用异步复位，很难在不影响模块功能的前提下将异步信号正确施加在这些模块。（Xilinx）

同步复位特点：

电路是百分之百同步化的
时钟可以充当同步复位信号的一个毛刺滤波，但如果毛刺发生在时钟触发边沿，flip-flop仍然可能出现亚稳态。
同步复位可能需要一个计数器来保障复位信号的宽度足够宽来实现有效的复位。
因为同步复位需要时钟来复位，有些极少数的情况下，如某些低功耗设计，时钟可能在复位前就被无效，那么同步复位也无效，这里可能只有异步复位有效。

异步复位优点

只要具有可复位的触发器，那么异步复位就可以生效

异步复位不会在数据路径引入其他逻辑

异步复位缺点

反断言阶段，即复位移除阶段，复位信号沿如果距离时钟触发沿很近，则可能发生亚稳态，那么复位状态可能会丢失，也就是常说的符合Recovery Time以及Removal Time（类似Setup Time和Hold Time）

板子的毛刺和噪声可能引起虚假复位。

其他的一些缺点已经在（同步复位相比较异步复位有以下特点）上面小节阐述。

注意：异步复位都应该同步释放，以处理可能出现的亚稳态和异常情况，如下面所示代码：

// 异步复位同步释放
module sync_reset #
(
    // depth of synchronizer
    parameter N = 2
)
(
    inputwire clk,
    inputwire rst,
    outputwire out
);

(* srl_style = "register" *)
reg [N-1:0] sync_reg = {N{1'b1}};

assign out = sync_reg[N-1];

always @(posedge clk orposedge rst) begin
    if (rst) begin
        sync_reg <= {N{1'b1}};
    endelsebegin
        sync_reg <= {sync_reg[N-2:0], 1'b0};
    end
end

endmodule
// 代码来自开源项目AlexForencich

如何去除不必要复位信号？

当需要去除一些复位信号时，直接注释掉相关的代码是不合适并且会引入非预期的结构以及会导致异常问题。如下面的代码，注释掉复位代码块里的din_dly1和din_dly2会让复位信号成为寄存器的使能信号，显然属于引入无关逻辑，可能会引起设计的问题。如图一为未注释代码前综合出的异步复位电路，图二为直接注释掉复位区域信号的代码。产生这种问题也很容易理解，代码逻辑就是非复位状态din_dly1和din_dly2才能工作。

always@(posedge sysclk orposedge rst)
begin
    if(rst)
    begin
//         din_dly1 <= 8'b0;
//         din_dly2 <= 8'b0;
         da_out <= 8'b0;
    end
    else
    begin
        din_dly1 <= da_in;
        din_dly2 <= din_dly1;
        da_out <= din_dly2;
    end
end

图一：未注释掉复位信号的代码
图二：注释掉复位信号的代码（引入非期望的电路）

当遇到需要去除一些寄存器的复位信号时，记住一个基本原则：一个时序模块不可以混合不同复位类型的寄存器，简单讲就是不能出现不复位的寄存器和复位的寄存器，只要使用复位信号，那么时序模块的寄存器都应该复位。那么需要去除一些寄存器的复位信号应该怎么办?同样功能的代码如下，将复位的寄存器放入一个always块中，不需要复位的寄存器放入另一个always块中。图三是实际综合出的电路也是实际期望的电路，没有引入其他逻辑。

always @(posedge sysclk) begin
    din_dly1 <= da_in;
    din_dly2 <= din_dly1;
end

always @(posedge sysclk orposedge rst) begin
    if(rst)
        da_out <= 8'b0;
    else
        da_out <= din_dly2;
    
end