二叉树
- 树的概念及结构
- 树的概念
- 树的相关概念
- 树的表示
- 二叉树的概念及结构
- 概念
- 特殊的二叉树
- 二叉树性质
- 二叉树的存储结构
- 二叉树的实现
- 二叉树顺序结构的实现
- 二叉树链式结构的实现
- 二叉树的遍历
- 前序遍历
- 中序遍历
- 后序遍历
- 二叉树结点数量
- 叶子结点数量
- 求树高
- 求k层结点数量
- 二叉树创建
- 二叉树销毁
- 层序遍历
- 判断是否是完全二叉树
树的概念及结构
树的概念
树是一种非线性的数据结构,它是由n(n>=0)个有限结点组成一个具有层次关系的集合。把它叫做树是因
为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。
有一个特殊的结点,称为根结点,根节点没有前驱结点
除根节点外,其余结点被分成M(M>0)个互不相交的集合T1、T2、……、Tm,其中每一个集合Ti(1<= i
<= m)又是一棵结构与树类似的子树。每棵子树的根结点有且只有一个前驱,可以有0个或多个后继
因此,树是递归定义的。

树的相关概念
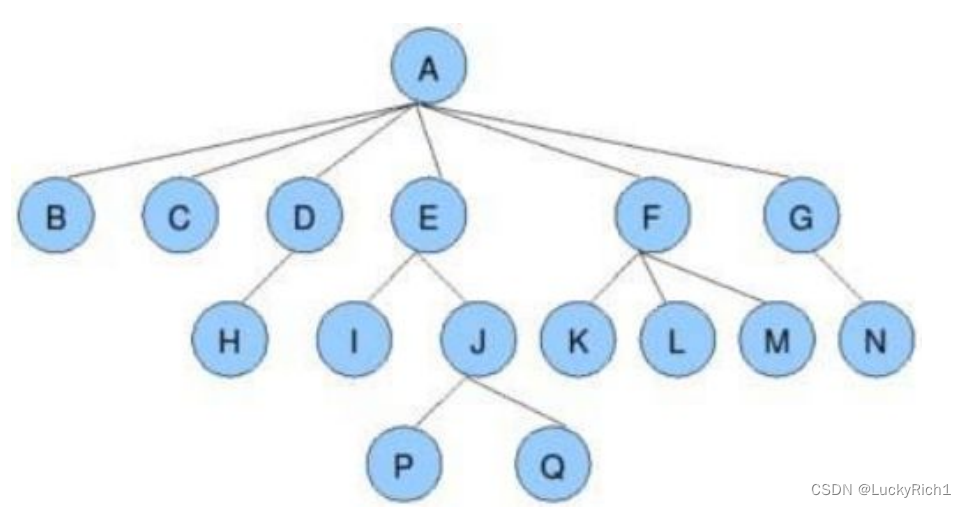
- 节点的度:一个节点含有的子树的个数称为该节点的度; 如上图:A的为6
- 叶节点或终端节点:度为0的节点称为叶节点;如上图:B、C、H、I…等节点为叶节点**
- 非终端节点或分支节点:度不为0的节点; 如上图:D、E、F、G…等节点为分支节点
- 双亲节点或父节点:若一个节点含有子节点,则这个节点称为其子节点的父节点; 如上图:A是B的父节点
- 孩子节点或子节点:一个节点含有的子树的根节点称为该节点的子节点; 如上图:B是A的孩子节点
- 兄弟节点:具有相同父节点的节点互称为兄弟节点; 如上图:B、C是兄弟节点
- 树的度:一棵树中,最大的节点的度称为树的度; 如上图:树的度为6
- 节点的层次:从根开始定义起,根为第1层,根的子节点为第2层,以此类推;
- 树的高度或深度:树中节点的最大层次;如上图:树的高度为4
- 堂兄弟节点:双亲在同一层的节点互为堂兄弟;如上图:H、I互为兄弟节点
- 节点的祖先:从根到该节点所经分支上的所有节点;如上图:A是所有节点的祖先
- 子孙:以某节点为根的子树中任一节点都称为该节点的子孙。如上图:所有节点都是A的子孙
- 森林:由m(m>0)棵互不相交的树的集合称为森林;
树的表示
树结构相对线性表就比较复杂了,要存储表示起来就比较麻烦了,既然保存值域,也要保存结点和结点之间
的关系,实际中树有很多种表示方式如:双亲表示法,孩子表示法、孩子双亲表示法以及孩子兄弟表示法
等。我们这里就简单的了解其中最常用的孩子兄弟表示法。
typedef int TDatatype;
typedef struct TreeNode
{
struct TreeNode* firstchild;//第一个孩子结点
struct TreeNode* pNextBrother;//指向下一个兄弟结点
TDatatype data;
};
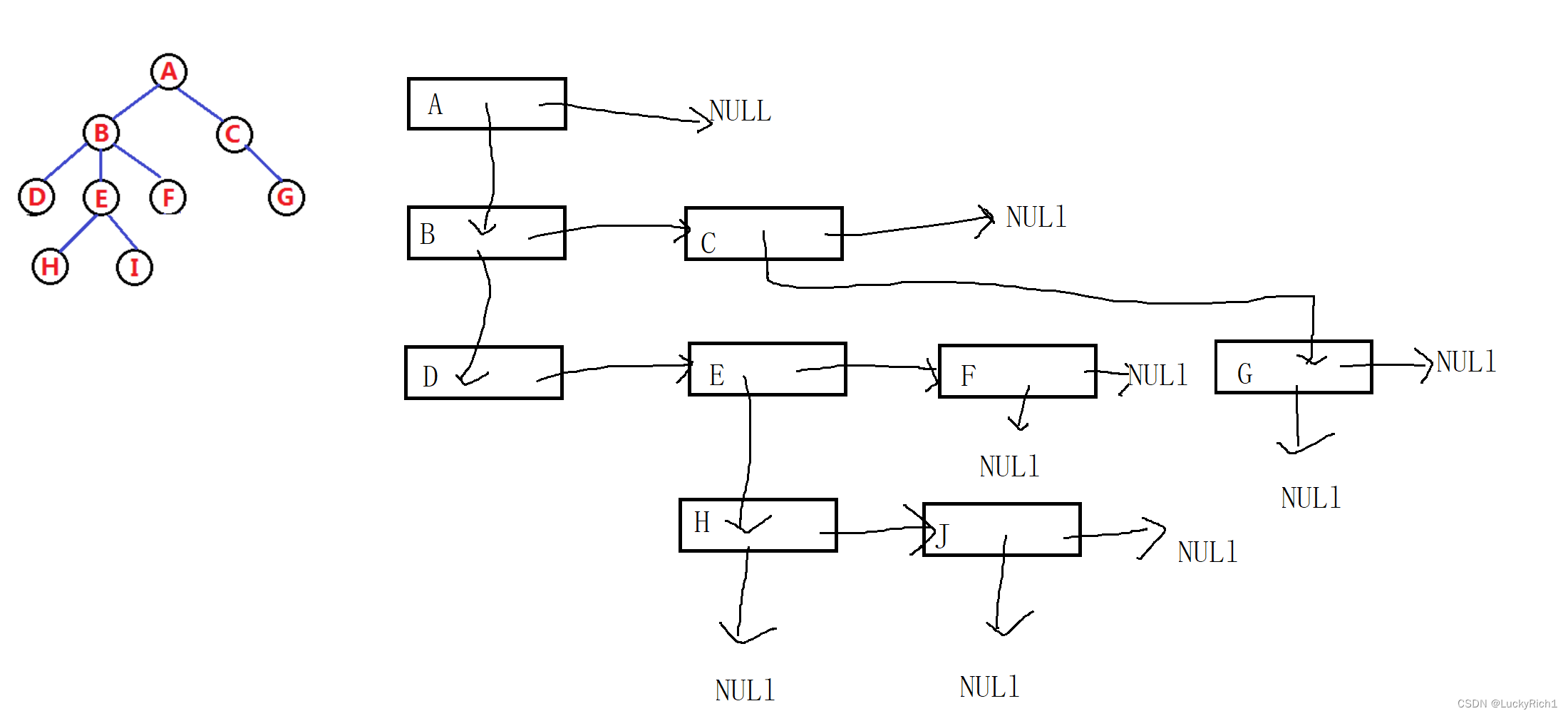
这样我们就把各结点关系通过孩子兄弟表示法表示了出来。如何把结点孩子打印出来呢?我们简单看一看方法,等以后在深究
void TreePrint(TreeNode* root)
{
if (root == NULL)
return;
TreeNode* cur = root->firstchild;
while (cur)
{
pirntf("%d ", root->data);
//递归
TreePrint(cur);
cur = cur->pNextBrother;
}
}
双亲表示法方便找双亲在哪里
二叉树的概念及结构
概念
一棵二叉树是结点的一个有限集合,该集合:
- 或者为空
- 由一个根节点加上两棵别称为左子树和右子树的二叉树组成
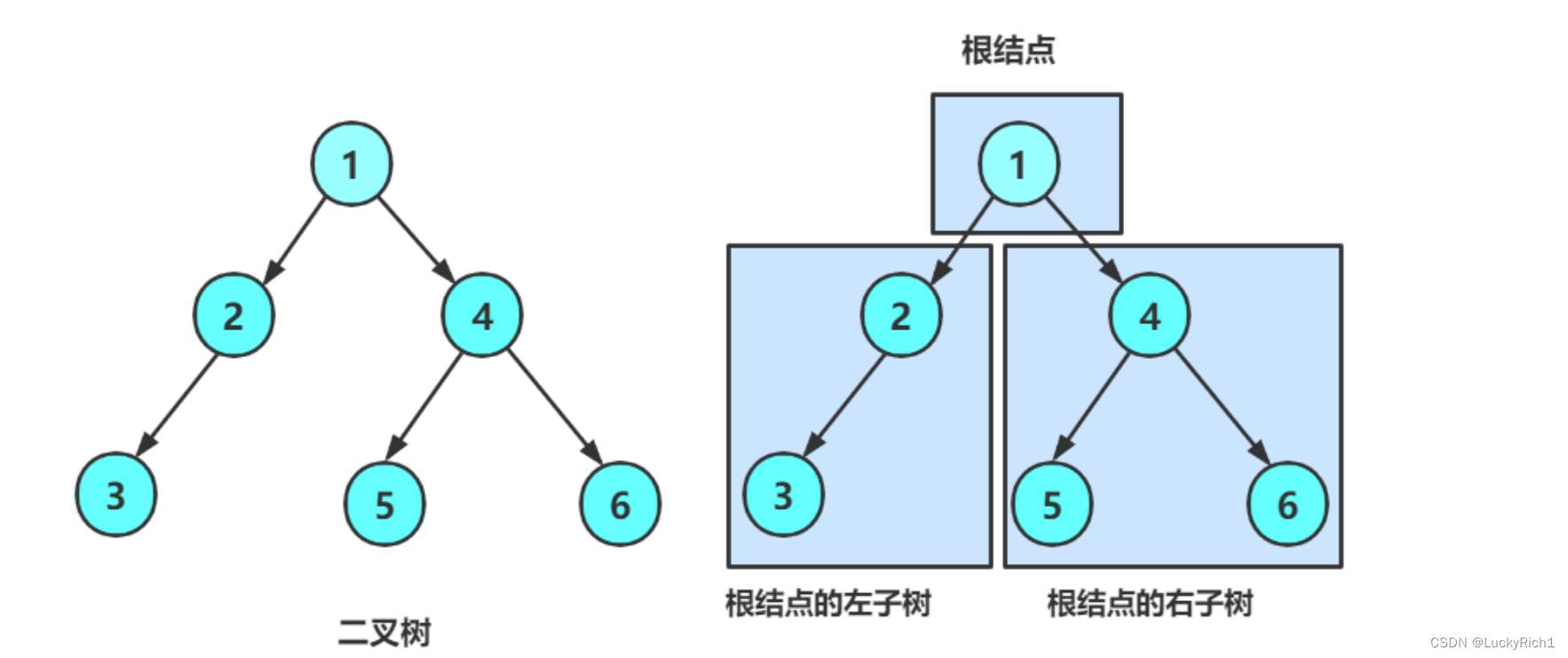
从上图可以看出:
- 二叉树不存在度大于2的结点
- 二叉树的子树有左右之分,次序不能颠倒,因此二叉树是有序树
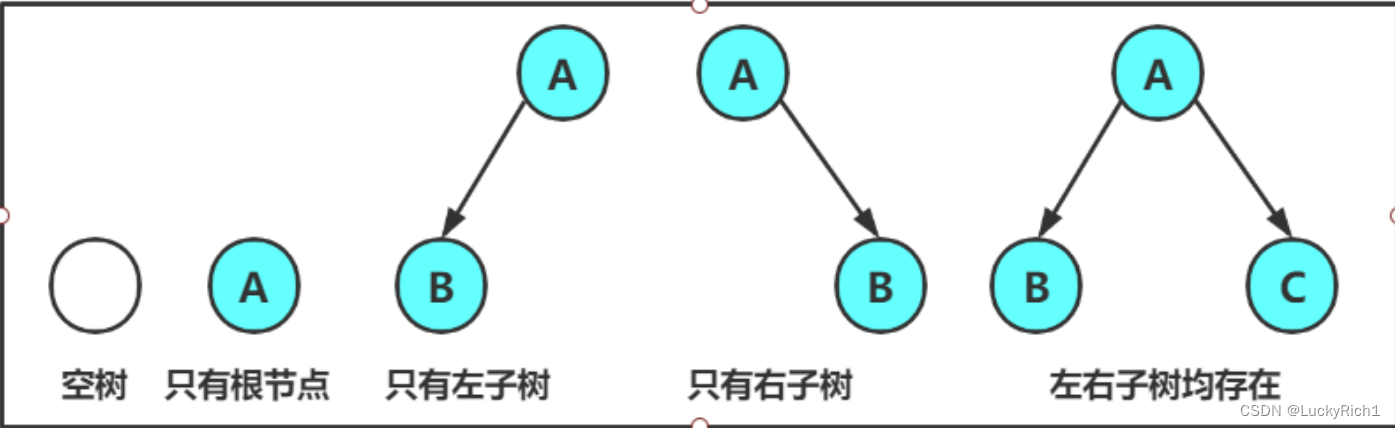
二叉树有五种形态
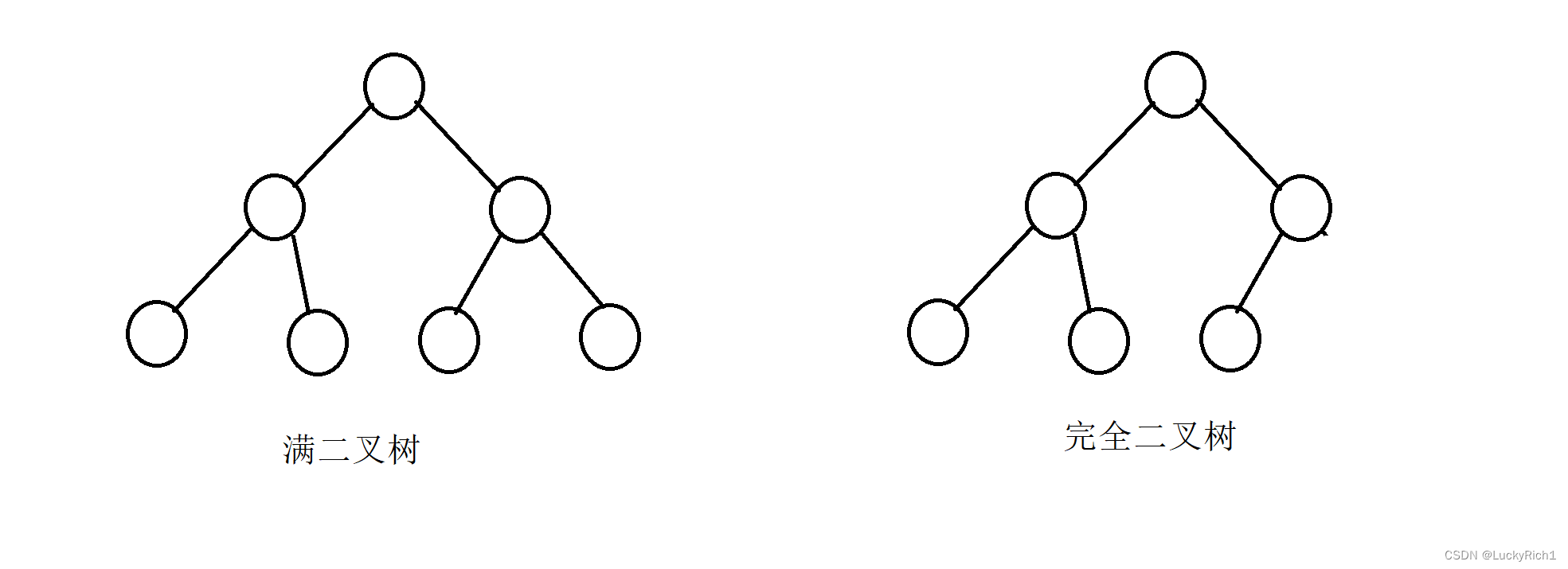
特殊的二叉树
- 满二叉树:一个二叉树,如果每一个层的结点数都达到最大值,则这个二叉树就是满二叉树。也就是
说,如果一个二叉树的层数为K,且结点总数是 ,则它就是满二叉树。 - 完全二叉树:完全二叉树是效率很高的数据结构,完全二叉树是由满二叉树而引出来的。对于深度为K
的,有n个结点的二叉树,当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对
应时称之为完全二叉树。 要注意的是满二叉树是一种特殊的完全二叉树。
二叉树性质
- 若规定根节点的层数为1,则一棵非空二叉树的第i层上最多有 2^(i-1)个结点.
- 若规定根节点的层数为1,则深度为h的二叉树的最大结点数是2^h-1个结点
- 对任何一棵二叉树, 如果度为0其叶结点个数为n0 , 度为2的分支结点个数为n2 ,则有 n0=n2 +1
- 若规定根节点的层数为1,具有n个结点的满二叉树的深度,h=log2(n+1) . (ps: 是log以2
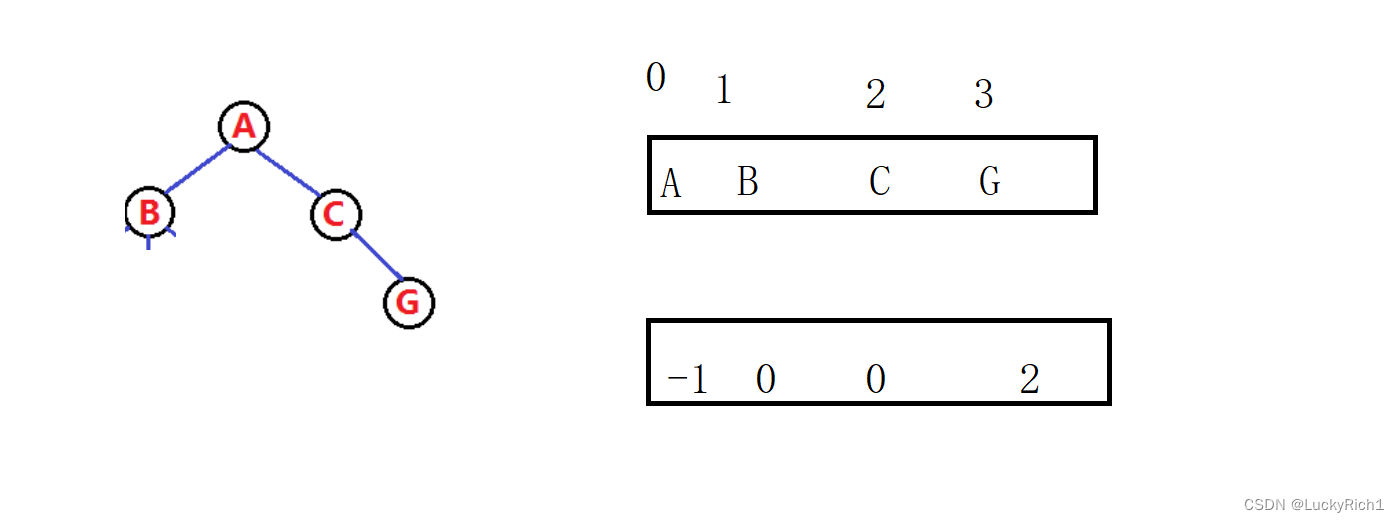
为底,n+1为对数) - 对于具有n个结点的完全二叉树,如果按照从上至下从左至右的数组顺序对所有节点从0开始编号,则对
于序号为i的结点有:
- 若i>0,i位置节点的双亲序号:(i-1)/2;i=0,i为根节点编号,无双亲节点
- 若2i+1<n,左孩子序号:2i+1,2i+1>=n否则无左孩子
- 若2i+2<n,右孩子序号:2i+2,2i+2>=n否则无右孩子
二叉树的存储结构
二叉树一般可以使用两种结构存储,一种顺序结构,一种链式结构。
- 顺序存储
顺序结构存储就是使用数组来存储,一般使用数组只适合表示完全二叉树(和满二叉树),因为不是完全二叉树会有空间的浪费。而现实中使用中只有堆才会使用数组来存储,关于堆的实现,在下面有介绍。,有兴趣可以看一看。二叉树顺序存储在物理上是一个数组,在逻辑上是一颗二叉树。
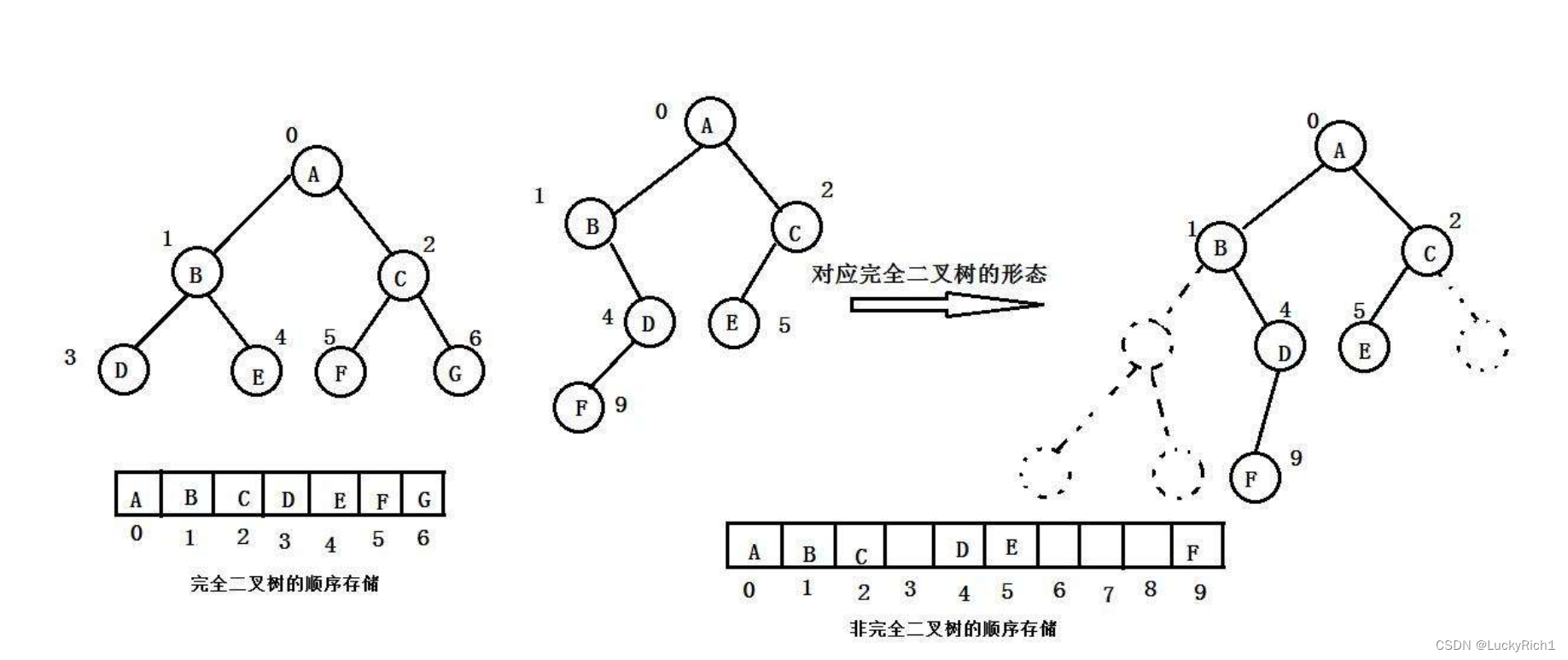
- 链式存储
二叉树的链式存储结构是指,用链表来表示一棵二叉树,即用链来指示元素的逻辑关系。 通常的方法是
链表中每个结点由三个域组成,数据域和左右指针域,左右指针分别用来给出该结点左孩子和右孩子所
在的链结点的存储地址 。链式结构又分为二叉链和三叉链,当前我们学习中一般都是二叉链。

二叉树的实现
二叉树顺序结构的实现
顺序结构存储一般堆会使用,下面详解讲解了堆。
堆的实现,画图和代码分析建堆,堆排序,时间复杂度以及TOP-K问题。
二叉树链式结构的实现
在学习二叉树的基本操作前,需先要创建一棵二叉树,然后才能学习其相关的基本操作。由于现在大家对二
叉树结构掌握还不够深入,为了降低大家学习成本,此处手动快速创建一棵简单的二叉树,快速进入二叉树
操作学习,等二叉树结构了解的差不多时,我们反过头再来研究二叉树真正的创建方式。
typedef int BTDataType;
typedef struct BTNode
{
int data;
struct BTNode* left;
struct BTNode* right;
}BTNode;
BTNode* CreateBTree()
{
BTNode* n1 = (BTNode*)malloc(sizeof(BTNode));
assert(n1);
BTNode* n2 = (BTNode*)malloc(sizeof(BTNode));
assert(n2);
BTNode* n3 = (BTNode*)malloc(sizeof(BTNode));
assert(n3);
BTNode* n4 = (BTNode*)malloc(sizeof(BTNode));
assert(n4);
BTNode* n5 = (BTNode*)malloc(sizeof(BTNode));
assert(n5);
BTNode* n6 = (BTNode*)malloc(sizeof(BTNode));
assert(n6);
BTNode* n7 = (BTNode*)malloc(sizeof(BTNode));
assert(n7);
n1->data = 1;
n2->data = 2;
n3->data = 3;
n4->data = 4;
n5->data = 5;
n6->data = 6;
n7->data = 7;
n1->left = n2;
n1->right = n4;
n2->left = n3;
n2->right = NULL;
n3->left = NULL;
n3->right = n7;
n4->left = n5;
n4->right = n6;
n5->left = NULL;
n5->right = NULL;
n6->left = NULL;
n6->right = NULL;
n7->left = NULL;
n7->right = NULL;
return n1;
}
二叉树的遍历
- 前序遍历(Preorder Traversal 亦称先序遍历)——访问根结点的操作发生在遍历其左右子树之前。
- 中序遍历(Inorder Traversal)——访问根结点的操作发生在遍历其左右子树之中(间)。
- 后序遍历(Postorder Traversal)——访问根结点的操作发生在遍历其左右子树之后。

二叉树遍历代码其实很简单,但是里面递归逻辑就不是这样了,因此需要真正遍历的顺序才行。要把空也带上,才能更好理解代码。
前序遍历
void PostOrder(BTNode* root)
{
if (root == NULL)
return;
PostOrder(root->left);
PostOrder(root->right);
printf("%d ", root->data);
}
我们来画一画递归展开图
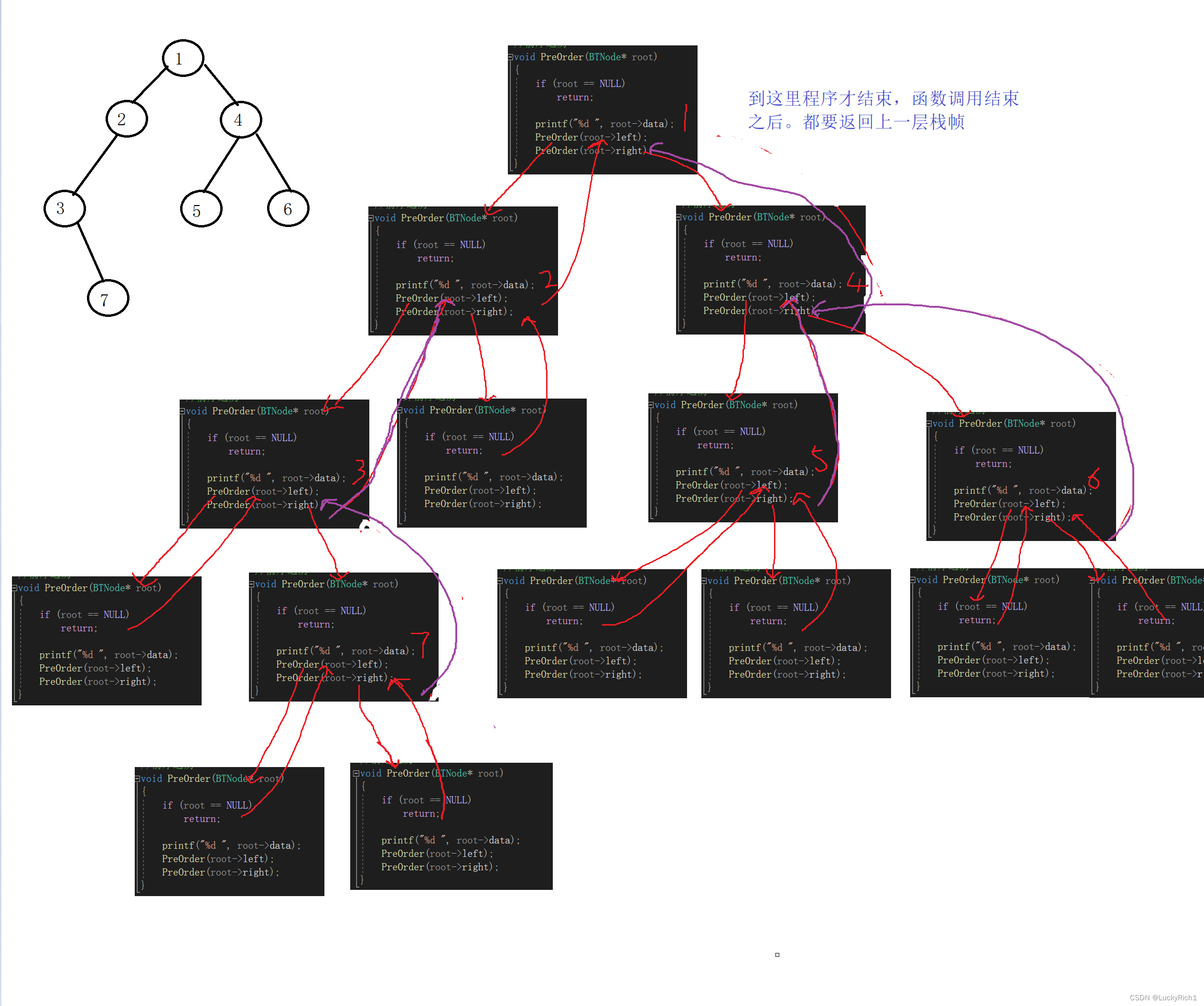
记住一个函数栈帧调用结束会返回到上一层。
中序遍历
void InOrder(BTNode* root)
{
if (root == NULL)
return;
InOrder(root->left);
printf("%d ", root->data);
InOrder(root->right);
}
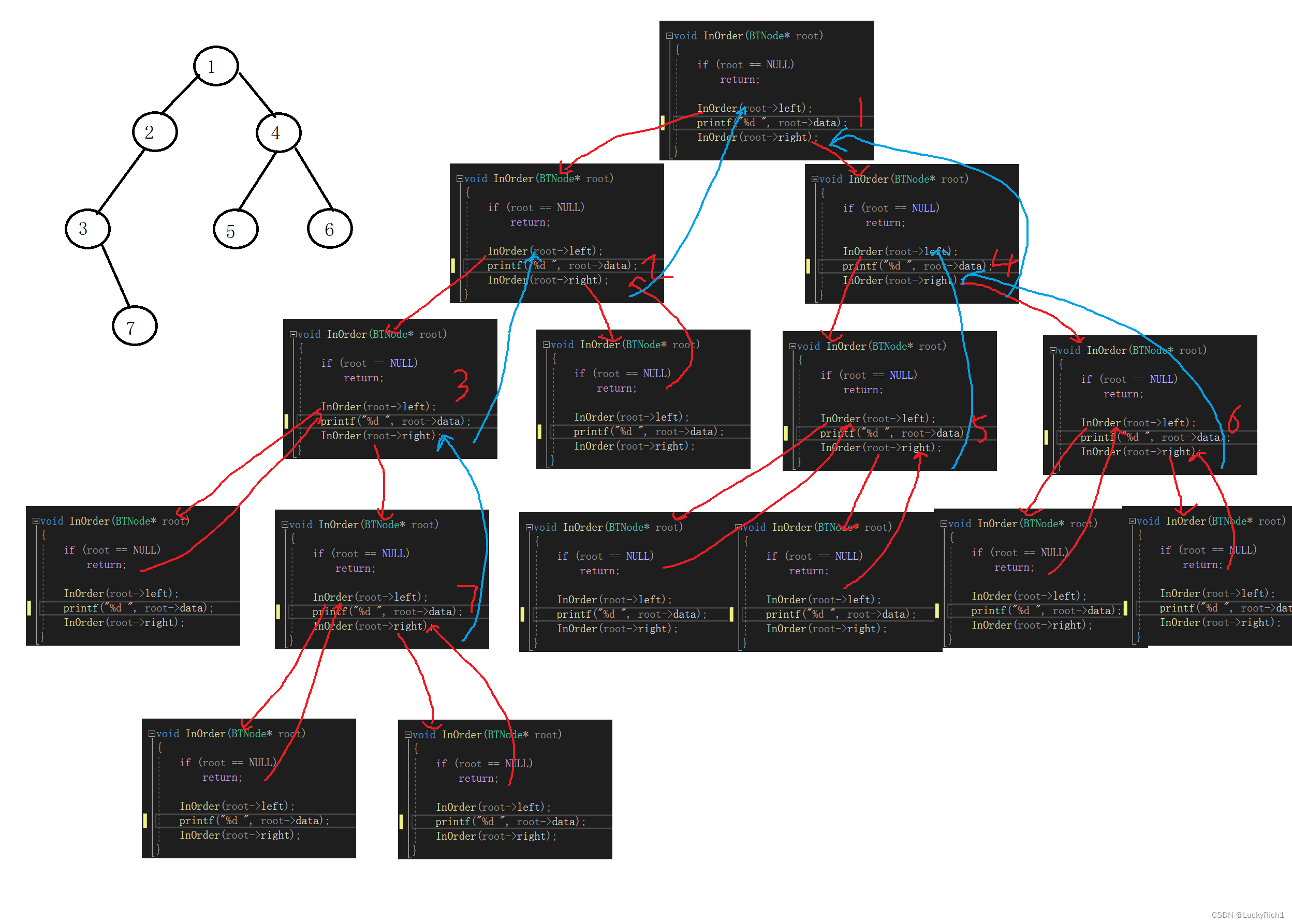
后序遍历
void PostOrder(BTNode* root)
{
if (root == NULL)
return;
PostOrder(root->left);
PostOrder(root->right);
printf("%d ", root->data);
}
这里递归展开图就不画了,有兴趣的可以自己画一下加深理解
二叉树结点数量
我们写二叉树代码的时候,一定要有分治的思想或者资本家的思想,分治思想是,处理好根这棵树,在处理左子树和右子树,而左子树和右子树又可以分成根左子树右子树,层层递归再返回。而资本家这个思想,假设董事长要经理统计员工多少人,经理让总监统计,总监让在下一级人统计。总之就是都是干一样的事,然后结果层层返回来。一定要有这个思想!!!
这个代码就是先统计左子树和右子树结点数量,然后再加上根自己。就是总结点数量。
int TreeSize(BTNode* root)
{
if (root == NULL)
return 0;
return TreeSize(root->left) + TreeSize(root->right)+1;
}
这里也可以用递归展开图看一看,但是呢,递归展开图是写出代码之后才能画的,再没有代码的时候,我们可以根据二叉树图把我们思想走一步。
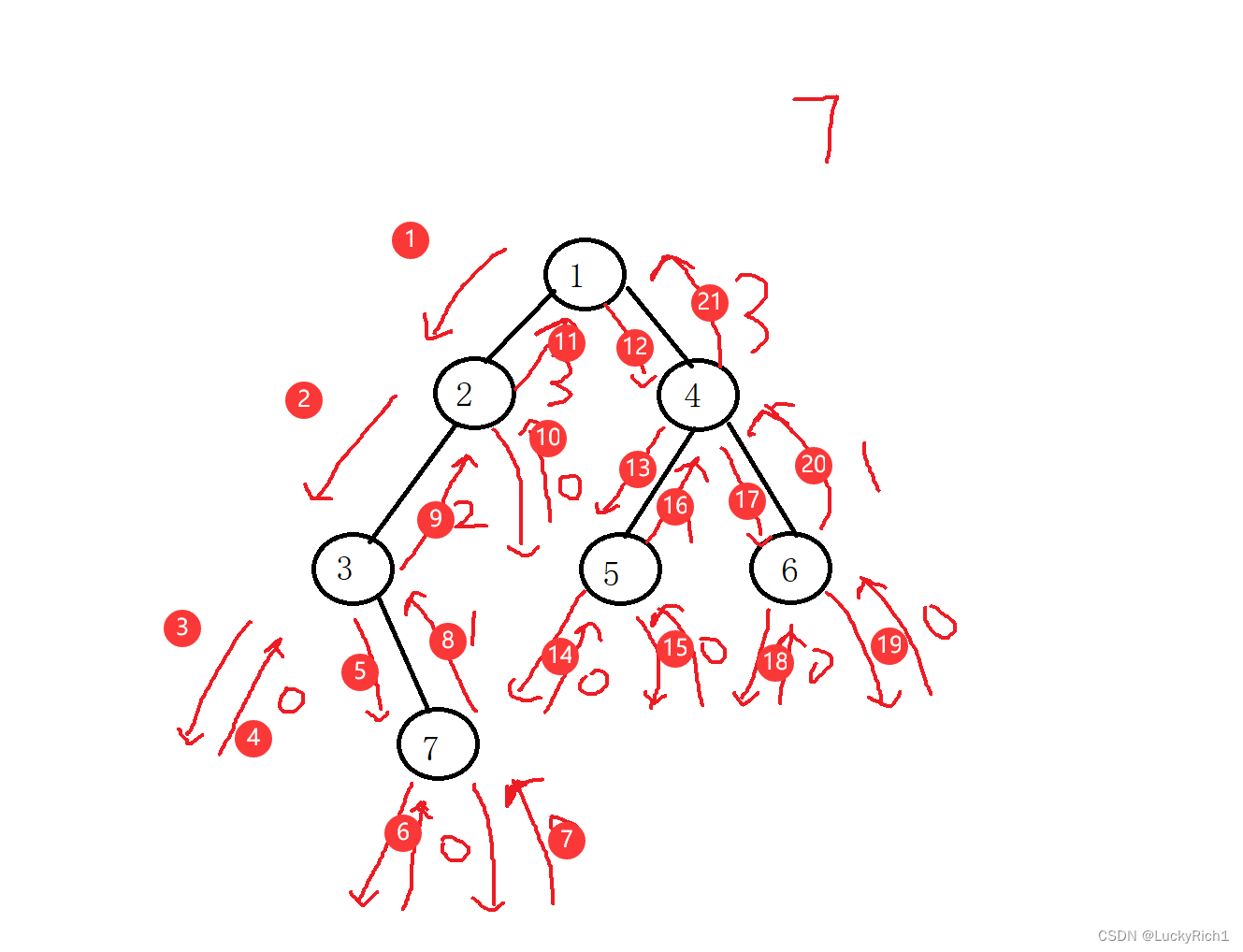
叶子结点数量
int TreeLeafSize(BTNode* root)
{
if (root == NULL)
return 0;
if (root->left == NULL && root->right == NULL)
return 1;
return TreeLeafSize(root->left) + TreeLeafSize(root->right);
}
求树高
思想:先求左子树高度,再求右子树高度,谁高,谁高度再加1就是树高
int TreeHigh(BTNode* root)
{
if (root == NULL)
return 0;
int lefthigh = TreeHigh(root->left);
int righthigh = TreeHigh(root->right);
return lefthigh > righthigh ? lefthigh + 1 : righthigh + 1;
}
求k层结点数量
思想:分治的思想转化为子问题,对于根来说是K层,对于左右子数来说是K-1层,然后层层递归。符合条件就返回。
int TreeKLevel(BTNode* root,int k)
{
if (root == NULL)
return 0;
if (k == 1)
return 1;
return TreeKLevel(root->left,k-1) + TreeKLevel(root->right,k-1);
}
为了方便就画了左边的递归展开图
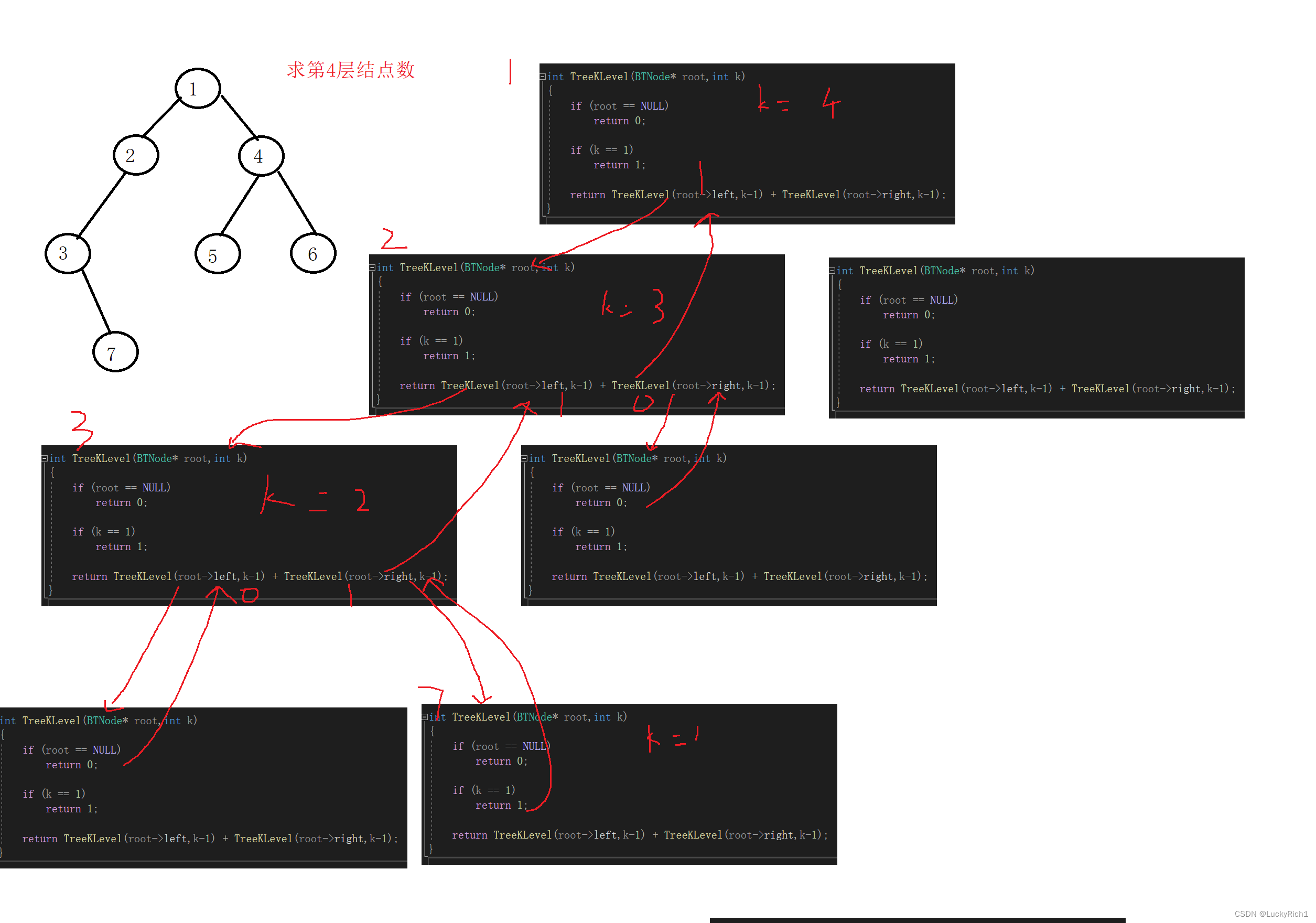
看了这一些题,应该对二叉树有更多了解了,下面我们学一学二叉树创建
二叉树创建
给这样**abc##de#g##f###**一个先序遍历数组(#代表为NULL),动态创建一颗二叉树

其实思想很简单,遇到结点就申请空间,然后把该结点左孩子和右孩子链接起来,再返回该结点。
BTNode* BinaryTreeCreate(char* a,int* pi)
{
if (a[*pi] == '#')
{
(*pi)++;
return NULL;
}
BTNode* root = (BTNode*)malloc(sizeof(BTNode));
if (root == NULL)
{
perror("mallo fail");
return NULL;
}
root->data = a[*pi];
(*pi)++;
root->left = BinaryTreeCreate(a, pi);
root->right = BinaryTreeCreate(a, pi);
return root;
}
有兴趣画个递归展开图加深理解。
二叉树销毁
思想:不能先销毁根结点,不然就找不到左子树和右子树了,所以先释放左子树和右子树再释放根结点;
void BinaryTreeDestroy(BTNode* root)
{
if (root == NULL)
return;
BinaryTreeDestroy(root->left);
BinaryTreeDestroy(root->right);
free(root);
}
这里用的是一级指针,root是形参,改变不了外面实参,如果外面的人调用这个参数,在外面把root置为NULL;如果想里面就把root置为空,就得传一级指针得地址,那么就得用二级指针来接受,里面可以在加个代码,root==NULL;具体原因看单链表的实现这一章,详细解释了原因。
层序遍历
思想:申请一个队列,先让根入队列,队列不为空,就出队列,然后把该结点的左孩子和右孩子入队列。
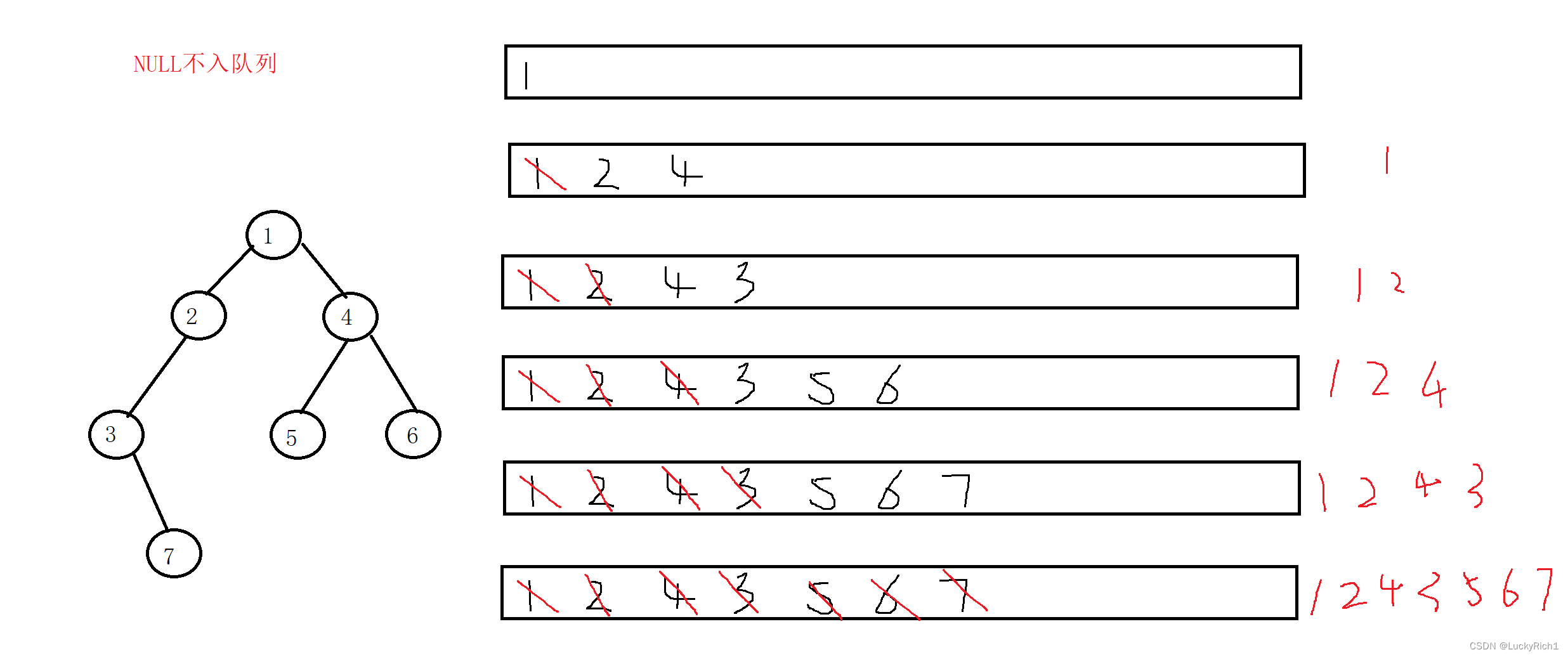
有一件事情要注意,我们入队列的是结点的指针。
void BinartLevelOrder(BTNode* root)
{
QE q;
QueueInit(&q);
//根入队列
QueuePush(&q, root);
while (!QueueEmpty(&q))
{
//出队列
BTNode* Front = QueueFront(&q);
QueuePop(&q);
printf("%d ", Front->data);
//左孩子不为空,入队列
if (Front->left)
QueuePush(&q, Front->left);
//右孩子不为空,入队列
if (Front->right)
QueuePush(&q, Front->right);
}
printf("\n");
QueueDestroy(&q);
}
判断是否是完全二叉树
什么是完全二叉树前面概念我们说过,下面有一些是完全二叉树,有些则不是
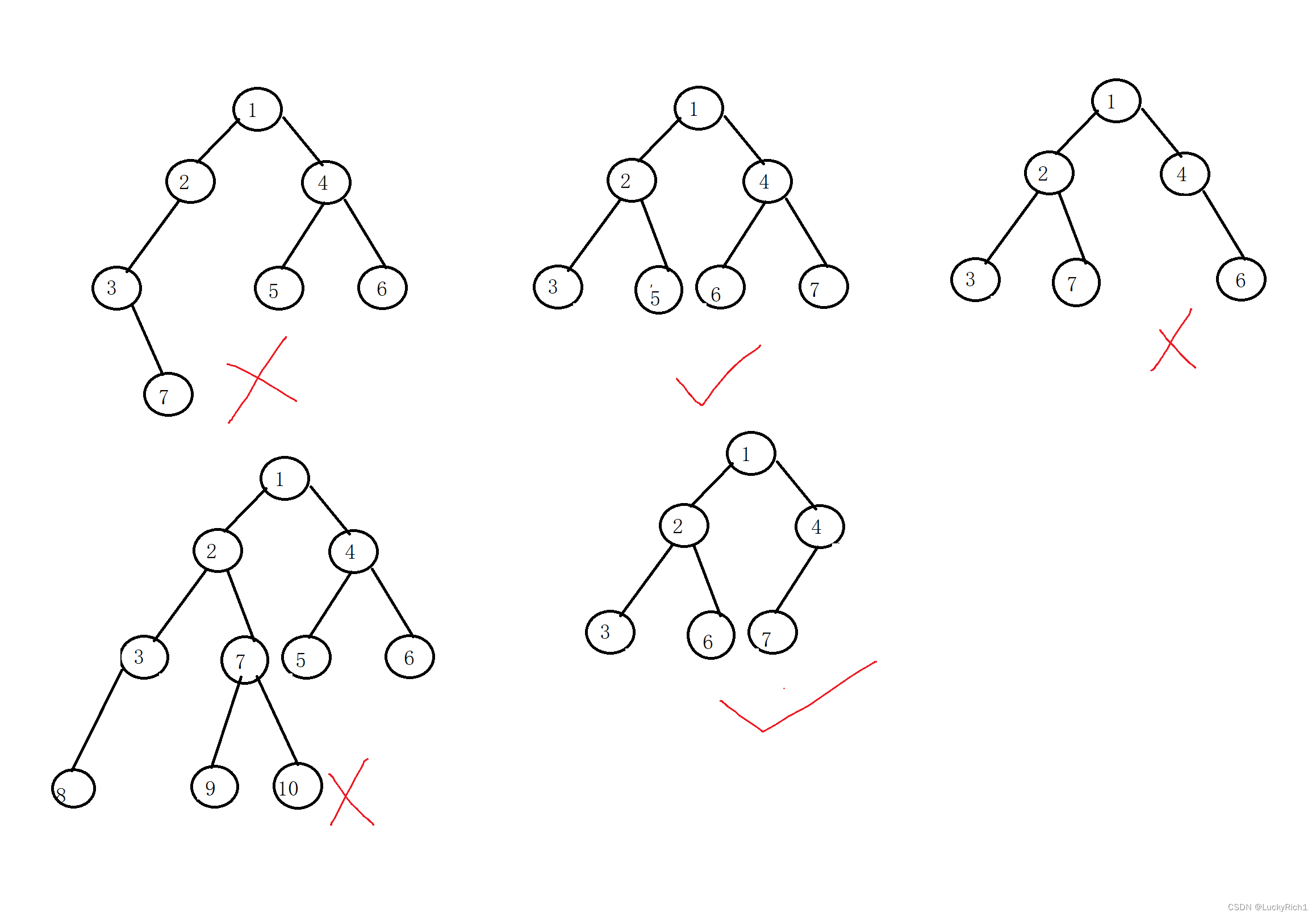
有人想用结点数判断,因为完全二叉树,h-1层是全满的,h层不满,但是上面第二张图每层结点都是满的,显示不能把结点数作为判断依据。
还有人这样想的,完全二叉树有且仅有一个度为1的结点,该结点只有左孩子没有右孩子,第四张图显然满足这个条件,但是它也不是颗完全二叉树。
下面介绍一种方法,还是用队列来帮助完成。
思想:一层一层走,遇到空以后,后续层序不能有非空,有非空就不是完全二叉树。


这里注意一点,队列结点和二叉树结点一定不能弄混了,我们入队列的是二叉树结点指针。
// 判断二叉树是否是完全二叉树
bool BinaryTreeComplete(BTNode* root)
{
QE q;
QueueInit(&q);
QueuePush(&q, root);
while (!QueueEmpty(&q))
{
BTNode* Front = QueueFront(&q);
QueuePop(&q);
//遇见空跳出循环
if (Front == NULL)
break;
//左右子树入队列,空也入
QueuePush(&q, Front->left);
QueuePush(&q, Front->right);
}
while (!QueueEmpty(&q))
{
BTNode* Front = QueueFront(&q);
QueuePop(&q);
//遇到空之后,再次遇到不为空,就不是完全二叉树
if (Front)
{
QueueDestroy(&q);
return false;
}
}
//一直为空,就是完全二叉树
QueueDestroy(&q);
return true;
}
至此关于二叉树概念,结构,实现,遍历等等写完了,后续还会更新红黑树和平衡二叉树,喜欢的可以点赞,收藏,加关注,以后比较着学。
关注小王不迷路,关键时候顶得住!