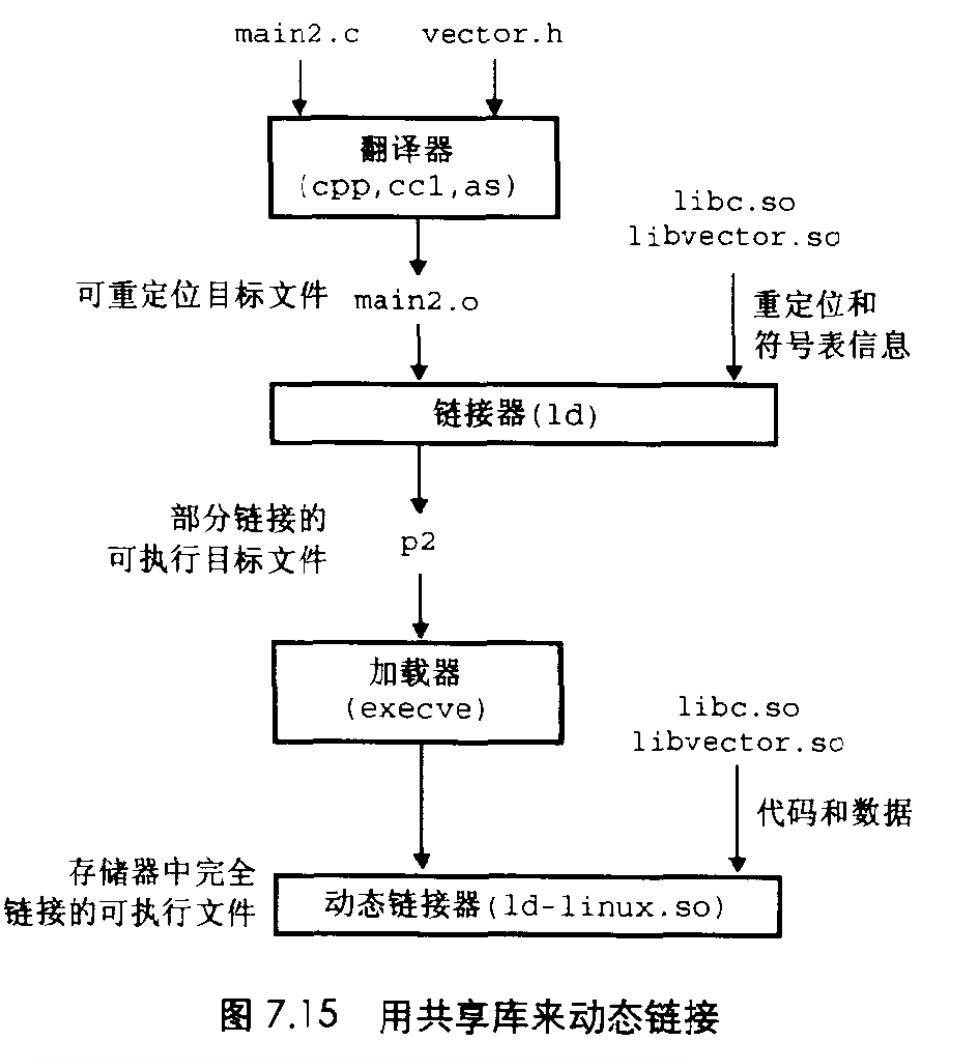
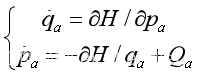理论力学专题:理论力学(物理类)框架
拉格朗日方程
虚位移:任意方向的微变化
- 约束分类:
- 稳定/不稳定(显含时间与否)
- 可解/不可解:
- 完整/微分约束:
- 几何约束(完整约束):约束方程不含速度项
- 运动约束(微分约束)
理想约束:\sum F_N\cdot \delta r = 0
- 将理想约束替换到牛顿第二定律中,将约束力分离,得到达朗贝尔方程:
- \sum(\vec{F}_i-m_i \ddot{\vec{r}}_i) \cdot \delta \vec{r}_i = 0
- 位矢固定时,得到虚功原理
广义坐标
- 自由度:独立坐标的个数
- 广义坐标:唯一能确定力学体系位置的独立变量
真实运动
- 例题:质量为m的质点,在重力场中以与水平线成a角的初速率v抛射,根据哈密顿原理,求质点的运动微分方程.
L = 1/2 m (\dot{x}^2 + \dot{y}^2) - mgy
- 作用量

拉格朗日方程
- 虚功原理:质点系的所有质点都处于平衡状态:\ddot{\vec{r}_i}=0
- \sum \vec{F_i}\cdot \delta \vec{r_i}
- 将坐标更改为独立的广义坐标后,定义广义力 Q_\alpha = \sum \vec{F}_i \cdot \partiial \vec{r}_i /\partial q_\alpha
- L = T - V
- 拉格朗日方程有哈密顿原理推导而来
- 拉格朗日方程: \frac{d}{dt}\frac{\partial L}{\partial \dot{q_\alpha}}-\frac{\partial L}{\partial q_\alpha} = Q_\alpha
- 最小作用量原理:\delta S = \delta \int_{t_1}^{t_2} Ldt = 0
对称与守恒
- 拉氏量中不显含的广义坐标称为循环坐标,运用对称性可推导出守恒定律
- 时间平移不变性----能量守恒
- 旋转不变形----动量守恒
- 空间平移不变性----总角动量守恒
刚体
- 刚体定轴运动的特殊广义坐标欧拉角:自转角,进动角,章动角
- 刚体运动角动量的确定

微振动
- 对多自由度系统振动的分析,主要突破口在于 简正坐标 和 简正模式
- 势能曲线分析
- 久期方程
哈密顿理论
- 任意拉格朗日函数加上一个时间的全导数后,仍可以满足原来的拉氏方程。广义坐标与广义动量(p_\alpha = \parital L/\partial \dot{q})出现了无数的对应方式
- 将拉格朗日函数替换掉,在保持广义动量与广义坐标的独立下,以正则共轭坐标描述系统。
- 新的哈密顿量 H(p,q,t) = \sum p_\alpha \dot{q_\alpha} - L
- 哈密顿方程