栈和队列的相关功能实现及其基础应用

news2024/11/27 16:48:12

       前言：栈和队列是常见的数据结构，它们在计算机科学中被广泛应用。栈和队列都是一些元素的集合，它们的主要区别在于数据的组织方式和访问顺序。在栈中，元素的添加和删除都在同一端进行，称为栈顶，而在队列中，元素的添加和删除分别在两端进行，分别称为队尾和队头。栈和队列在算法设计和程序开发中都有着重要的作用，比如在计算表达式的值时可以使用栈，而在网络数据传输时则常常使用队列。本文将重点介绍栈和队列的实现，以及利用它们解决各种问题的思路。

 

目录

1.栈和队列的概念

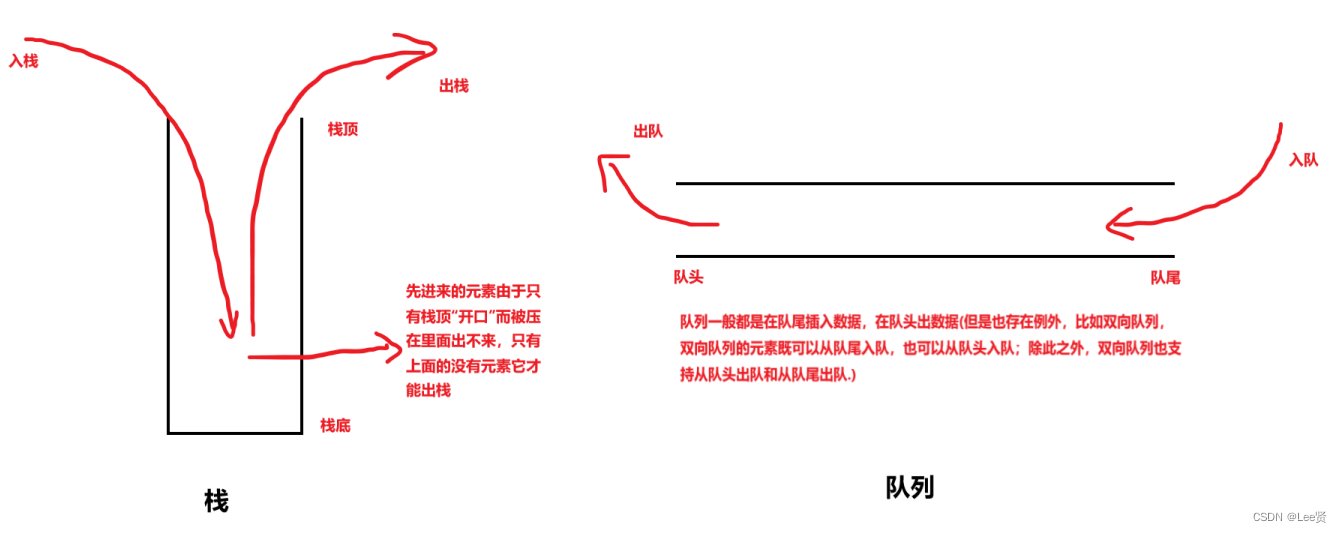
栈的“先进后出”与 队列的"先进先出"

2.栈和队列的功能简介与实现

2.1栈的功能实现

2.1.1 结构体定义与初始化栈

 2.1.2 入栈、出栈和查询等操作

2.2 队列的功能实现

2.2.1 队列的结构体定义和初始化

2.2.2 队列的入、出队和查询队头、尾等操作

3.源码及测试代码

Stack.h

Stack.cpp

Queue.h

Queue.cpp

Test.cpp

3.栈和队列的相关基础应用

3.1 括号匹配问题

思路分析：

代码实现：

3.2 表达式求值问题

3.3 用队列实现栈

思路分析： 

 代码实现：

3.4 没错，用栈实现队列

思路分析：

代码实现：

3.5 设计循环队列

思路分析：

代码实现：

总结：

4.金句频道

1.栈和队列的概念

栈的“先进后出”与 队列的"先进先出"

      栈是一种“后进先出”（Last In, First Out）的数据结构，也就是说最后进入栈中的元素最先弹出。在栈中只允许在一端进行插入和删除操作，这一端被称为栈顶。插入元素的操作被称为入栈，删除元素的操作被称为出栈。栈常用于实现递归算法、表达式求值、函数调用栈等。

      而队列则是一种“先进先出”（First In, First Out）的数据结构，也就是说最先进入队列的元素最先删除。队列有两个端点，分别为队头和队尾。数据插入在队尾，删除在队头，这就保证了队列的元素按照先进先出的顺序进行处理。队列常用于实现广度优先搜索（BFS）算法、仿真模拟等。

 

2.栈和队列的功能简介与实现

2.1栈的功能实现

      栈可以进行插入、删除、查询操作。栈具有“后进先出”的特点，即最后压入栈的元素最先被弹出。在 C 语言中，可以使用数组或链表来实现一个简单的栈。因为，我们的数组和栈的先入后出的逻辑相符合，所以，在实践中，我们一般使用动态开辟的顺序表来模拟实现栈及其相关功能。

2.1.1 结构体定义与初始化栈

定义一个数组和一个栈顶指针。栈顶指针初始化为 0，表示栈为空。

typedef int STDataType;
typedef struct Stack
{
	STDataType* a;
	int top;//栈顶
	int capacity;//容量
}ST;

void STInit(ST* pst)
{
	assert(pst);//先断言一下，防止为空指针
	pst->a = NULL;
	pst->top = 0;//如果让top初始化为-1，那么就相当于top直接指向栈顶元素，这样不利于我们在空间已满时realloc空间的判断，所以我们选择初始时就让top指向栈顶元素的下一个元素(初始相当于栈顶下标为-1)
	pst->capacity = 0;
}

 2.1.2 入栈、出栈和查询等操作

注意要先判断是否合法，包括入栈时先判断数组是否已满，出栈时栈是否为空等。

void STDestroy(ST* pst)
{
	assert(pst);
	free(pst->a);
	pst->a = NULL;//释放后不要忘记置空，防止其成为野指针
	pst->capacity = pst->top = 0;
}
bool STEmpty(ST* pst)
{
	assert(pst);
	return pst->top == 0;
}
void STPush(ST* pst, STDataType x)
{
	//先判断是否需要扩容
	if (pst->capacity == pst->top)
	{
		int newcapacity = 2 * pst->capacity + 10;//加上10的目的是为了防止pst->capacity=0的情况
		STDataType* temp = (STDataType*)realloc(pst->a,sizeof(int) * newcapacity);
		//如果开辟不成功
		if (!temp)
		{
			perror("开辟未成功\n");
			return;
		}
		pst->a = temp;
		pst->capacity = newcapacity;
	}
	pst->a[pst->top++] = x;
}


void STPop(ST* pst)
{
	assert(pst);
	//先判断是否为空
	assert(!STEmpty(pst));

	pst->top--;
}

STDataType STTop(ST* pst)
{
	assert(pst);
	//先判断是否为空
	assert(!STEmpty(pst));

	return pst->a[(pst->top) - 1];
}

2.2 队列的功能实现

        队列的功能与栈类似，也需要增删和插入等操作，也可以用数组或链表来实现，为了使空间利用率更高，这里我们用链表的方式来实现。

2.2.1 队列的结构体定义和初始化

       我们知道，队列是由队头和队尾控制，所以我们可以将每个数据设置为结构体，将队列设置为队尾和队头的两个指针，再加上数据实际存储量，以便于求size。

typedef int QDataType;
typedef struct QueueNode
{
	struct QueueNode* next;
	QDataType data;
}QNode;

typedef struct Queue
{
	QNode* phead;
	QNode* ptail;
	int size;
}Queue;

void QueueInit(Queue* pq)
{
	assert(pq);
	pq->phead = pq->ptail = NULL;
	pq->size = 0;
}

2.2.2 队列的入、出队和查询队头、尾等操作

还是要注意对可能存在非法的位置处进行判断即可。

void QueuePush(Queue* pq, QDataType x)
{
	//如果是插入第一个元素，那么头指针和尾指针一样
	if (pq->phead==NULL)
	{
		pq->ptail = (QNode*)malloc(sizeof(QNode));
		pq->ptail->data = x;
		pq->ptail->next = NULL;
		pq->phead = pq->ptail;
	}
	else
	{
		QNode* temp = (QNode*)malloc(sizeof(QNode));
		temp->data = x;
		temp->next = NULL;
		pq->ptail->next = temp;
		//此时不能再将phead赋值成ptail，因为ptail是指向尾部的指针，phead是指向头部的指针，初始时赋值为ptail，此后ptail向后移动，phead的值保持不变以维持队列的头一直是第一个入队元素
		pq->ptail = temp;//重新指向尾部
	}
	pq->size++;
}
void QueuePop(Queue* pq)
{
	assert(pq);
	assert(!QueueEmpty(pq));
	//当只有一个节点时
	if (pq->phead->next== NULL)
	{
		free(pq->phead);
		pq->phead = pq->ptail = NULL;
		pq->size = 0;
	}
	else
	{
		QNode* temp = pq->phead->next;
		free(pq->phead);
		pq->phead = temp;
		pq->size--;
	}
}
QDataType QueueFront(Queue* pq)
{
	assert(pq);
	assert(!QueueEmpty(pq));
	return pq->phead->data;
}
QDataType QueueBack(Queue* pq)
{
	assert(pq);
	assert(!QueueEmpty(pq));
	return pq->ptail->data;
}

3.源码及测试代码

Stack.h

#pragma once
#include<stdlib.h>
#include<assert.h>
#include<stdbool.h>

typedef int STDataType;
typedef struct Stack
{
	STDataType* a;
	int top;//栈顶
	int capacity;//容量
}ST;
// 初始化栈
void STInit(ST* pst);
// 销毁栈
void STDestroy(ST* pst);
// 入栈
void STPush(ST* pst, STDataType x);
// 出栈
void STPop(ST* pst);
// 获取栈顶元素
STDataType STTop(ST* pst);
// 检测栈是否为空，如果为空返回非零结果，如果不为空返回0 
bool STEmpty(ST* pst);
//获取栈的大小
int STSize(ST* pst);

Stack.cpp

#include "Stack.h"


void STInit(ST* pst)
{
	assert(pst);//先断言一下，防止为空指针
	pst->a = NULL;
	pst->top = 0;//如果让top初始化为-1，那么就相当于top直接指向栈顶元素，这样不利于我们在空间已满时realloc空间的判断，所以我们选择初始时就让top指向栈顶元素的下一个元素(初始相当于栈顶下标为-1)
	pst->capacity = 0;
}

void STDestroy(ST* pst)
{
	assert(pst);
	free(pst->a);
	pst->a = NULL;//释放后不要忘记置空，防止其成为野指针
	pst->capacity = pst->top = 0;
}
bool STEmpty(ST* pst)
{
	assert(pst);
	return pst->top == 0;
}
void STPush(ST* pst, STDataType x)
{
	//先判断是否需要扩容
	if (pst->capacity == pst->top)
	{
		int newcapacity = 2 * pst->capacity + 10;//加上10的目的是为了防止pst->capacity=0的情况
		STDataType* temp = (STDataType*)realloc(pst->a,sizeof(int) * newcapacity);
		//如果开辟不成功
		if (!temp)
		{
			perror("开辟未成功\n");
			return;
		}
		pst->a = temp;
		pst->capacity = newcapacity;
	}
	pst->a[pst->top++] = x;
}


void STPop(ST* pst)
{
	assert(pst);
	//先判断是否为空
	assert(!STEmpty(pst));

	pst->top--;
}

STDataType STTop(ST* pst)
{
	assert(pst);
	//先判断是否为空
	assert(!STEmpty(pst));

	return pst->a[(pst->top) - 1];
}

int STSize(ST* pst)
{
	assert(pst);
	return pst->top;
}

Queue.h

#pragma once
#include<stdlib.h>
#include<assert.h>
#include<stdbool.h>

typedef int QDataType;
typedef struct QueueNode
{
	struct QueueNode* next;
	QDataType data;
}QNode;

typedef struct Queue
{
	QNode* phead;
	QNode* ptail;
	int size;
}Queue;

// 初始化队列
void QueueInit(Queue* pq);
//销毁队列
void QueueDestroy(Queue* pq);
// 队尾入队列
void QueuePush(Queue* pq, QDataType x);
// 队头出队列
void QueuePop(Queue* pq);
// 获取队列头部元素
QDataType QueueFront(Queue* pq);
// 获取队列尾部元素
QDataType QueueBack(Queue* pq);
//获取队列的大小
int QueueSize(Queue* pq);
//判断队列是否为空
bool QueueEmpty(Queue* pq);

Queue.cpp

#include "Queue.h"


void QueueInit(Queue* pq)
{
	assert(pq);
	pq->phead = pq->ptail = NULL;
	pq->size = 0;
}
void QueueDestroy(Queue* pq)
{
	assert(pq);
	QNode* p = pq->phead;
	while (p)
	{
		QNode* next = p->next;
		free(p);
		p = next;
	}

	pq->phead = pq->ptail = NULL;
	pq->size = 0;
}
void QueuePush(Queue* pq, QDataType x)
{
	//如果是插入第一个元素，那么头指针和尾指针一样
	if (pq->phead==NULL)
	{
		pq->ptail = (QNode*)malloc(sizeof(QNode));
		pq->ptail->data = x;
		pq->ptail->next = NULL;
		pq->phead = pq->ptail;
	}
	else
	{
		QNode* temp = (QNode*)malloc(sizeof(QNode));
		temp->data = x;
		temp->next = NULL;
		pq->ptail->next = temp;
		//此时不能再将phead赋值成ptail，因为ptail是指向尾部的指针，phead是指向头部的指针，初始时赋值为ptail，此后ptail向后移动，phead的值保持不变以维持队列的头一直是第一个入队元素
		pq->ptail = temp;//重新指向尾部
	}
	pq->size++;
}
void QueuePop(Queue* pq)
{
	assert(pq);
	assert(!QueueEmpty(pq));
	//当只有一个节点时
	if (pq->phead->next== NULL)
	{
		free(pq->phead);
		pq->phead = pq->ptail = NULL;
		pq->size = 0;
	}
	else
	{
		QNode* temp = pq->phead->next;
		free(pq->phead);
		pq->phead = temp;
		pq->size--;
	}
}
QDataType QueueFront(Queue* pq)
{
	assert(pq);
	assert(!QueueEmpty(pq));
	return pq->phead->data;
}
QDataType QueueBack(Queue* pq)
{
	assert(pq);
	assert(!QueueEmpty(pq));
	return pq->ptail->data;
}
int QueueSize(Queue* pq)
{
	assert(pq);
	return pq->size;
}
bool QueueEmpty(Queue* pq)
{
	assert(pq);
	return pq->size == 0;
}

Test.cpp

#include<stdio.h>
#include"Stack.h"
#include"Queue.h"


void TestStack1()
{
	ST st;
	STInit(&st);
	STPush(&st, 1);
	STPush(&st, 2);
	printf("%d\n", STTop(&st));
	STPop(&st);

	STPush(&st, 3);
	STPush(&st, 4);
	while (!STEmpty(&st))
	{
		printf("%d ", STTop(&st));
		STPop(&st);
	}

	STDestroy(&st);
}

void TestQueue()
{
	Queue pq;
	QueueInit(&pq);
	QueuePush(&pq, 1);
	QueuePush(&pq, 2);
	printf("%d\n", QueueFront(&pq));
	QueuePop(&pq);
	QueuePush(&pq, 3);
	QueuePush(&pq, 4);
	while (!QueueEmpty(&pq))
	{
		printf("%d ", QueueFront(&pq));
		printf("%d\n", QueueBack(&pq));
		QueuePop(&pq);
	}
	QueueDestroy(&pq);
}
int main()
{
	printf("栈测试:->\n");
	TestStack1();
	printf("\n队列测试:->\n");
	TestQueue();
	return 0;
}

3.栈和队列的相关基础应用

3.1 括号匹配问题

思路分析：

       对于我们的任意一个字符串，我们需要判断他们的括号是否匹配，我们遍历给定的字符串 s。当我们遇到一个左括号时，我们会期望在后续的遍历中，有一个相同类型的右括号将其闭合。由于后遇到的左括号要先闭合，因此我们可以将这个左括号放入栈顶。

       当我们遇到一个右括号时，我们需要将一个相同类型的左括号闭合。此时，我们可以取出栈顶的左括号并判断它们是否是相同类型的括号。如果不是相同的类型，或者栈中并没有左括号，那么字符串 s 无效，返回 False。

      在遍历结束后，如果栈中没有左括号，说明我们将字符串 s 中的所有左括号闭合，返回 True，否则返回 False。

      注意到有效字符串的长度一定为偶数，因此如果字符串的长度为奇数，我们可以直接返回 False，也可以省去后续的遍历判断过程。

代码实现：

typedef char STDataType;
typedef struct Stack
{
	STDataType* a;
	int top;//栈顶
	int capacity;//容量
}ST;
void STInit(ST* pst)
{
	assert(pst);//先断言一下，防止为空指针
	pst->a = NULL;
	pst->top = 0;//如果让top初始化为-1，那么就相当于top直接指向栈顶元素，这样不利于我们在空间已满时realloc空间的判断，所以我们选择初始时就让top指向栈顶元素的下一个元素(初始相当于栈顶下标为-1)
	pst->capacity = 0;
}

void STDestroy(ST* pst)
{
	assert(pst);
	free(pst->a);
	pst->a = NULL;//释放后不要忘记置空，防止其成为野指针
	pst->capacity = pst->top = 0;
}
bool STEmpty(ST* pst)
{
	assert(pst);
	return pst->top == 0;
}
void STPush(ST* pst, STDataType x)
{
	//先判断是否需要扩容
	if (pst->capacity == pst->top)
	{
		int newcapacity = 2 * pst->capacity + 10;//加上10的目的是为了防止pst->capacity=0的情况
		STDataType* temp = (STDataType*)realloc(pst->a,sizeof(int) * newcapacity);
		//如果开辟不成功
		if (!temp)
		{
			perror("开辟未成功\n");
			return;
		}
		pst->a = temp;
		pst->capacity = newcapacity;
	}
	pst->a[pst->top++] = x;
}
void STPop(ST* pst)
{
	assert(pst);
	//先判断是否为空
	assert(!STEmpty(pst));

	pst->top--;
}

STDataType STTop(ST* pst)
{
	assert(pst);
	//先判断是否为空
	assert(!STEmpty(pst));

	return pst->a[(pst->top) - 1];
}

int STSize(ST* pst)
{
	assert(pst);
	return pst->top;
}

class Solution {
public:
    bool isValid(string s) {
        ST pst;
        STInit(&pst);
        int len=s.length();
        for(int i=0;i<len;i++)
        {
            if(s[i]=='('||s[i]=='{'||s[i]=='[')
             {
                 STPush(&pst,s[i]);
             }
            else if(s[i]==')')
            {
                if(!STEmpty(&pst)&&STTop(&pst)=='(')//先判断是否为空再判断队首元素，尽管队首元素里有判断是否为空，但是assert函数会强制中断程序，导致出错
                  STPop(&pst);
                else// 如果不匹配，可以直接返回false
                  return false;

            }
            else if(s[i]=='}')
            {
                if(!STEmpty(&pst)&&STTop(&pst)=='{')
                  STPop(&pst);
                else
                  return false;
            }
            else if(s[i]==']')
            {
                if(!STEmpty(&pst)&&STTop(&pst)=='[')
                  STPop(&pst);
                else
                  return false;
            }
            
        }
        if(!STEmpty(&pst))
           return false;
        return true;
    }
};

3.2 表达式求值问题

这个问题由于实现起来过于复杂繁琐，目前更加推荐有一定STL基础的同学来参考，不过靠上面给出的代码，完全可以用纯C实现，只是会过于繁琐，这里我就不在展开，详情请前往表达式求值问题-双栈模板化实现。

3.3 用队列实现栈

思路分析： 

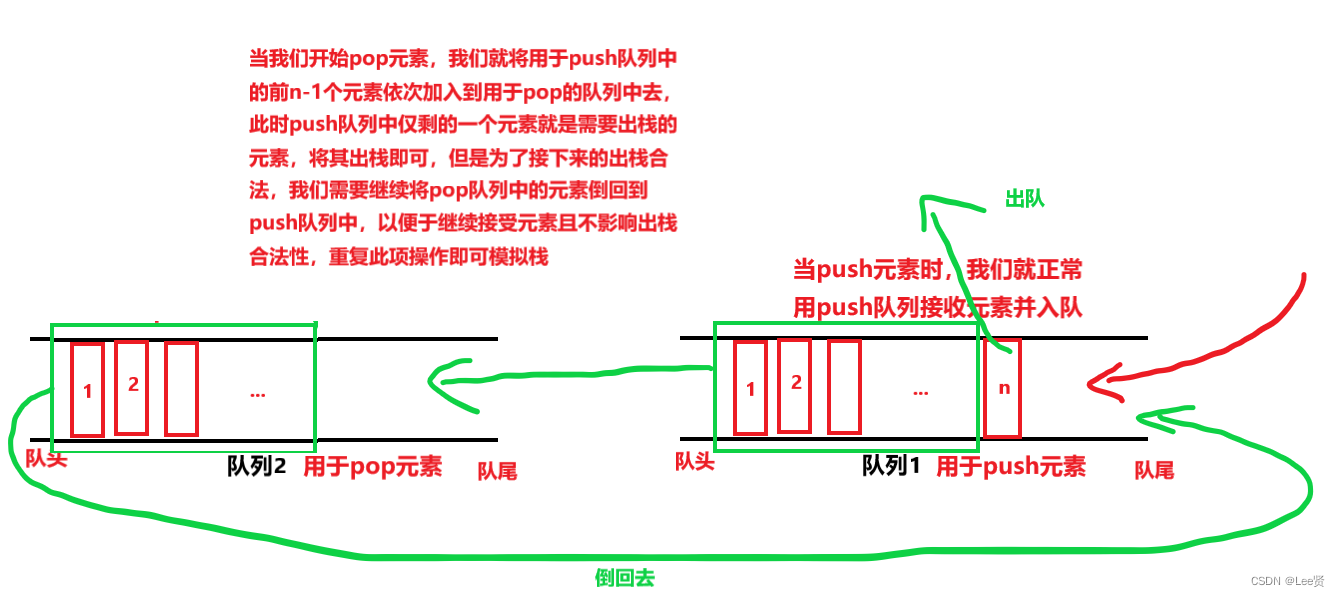
 代码实现：

typedef int QDataType;
typedef struct QueueNode
{
	struct QueueNode* next;
	QDataType data;
}QNode;

typedef struct Queue
{
	QNode* phead;
	QNode* ptail;
	int size;
}Queue;

void QueueInit(Queue* pq)
{
	assert(pq);
	pq->phead = pq->ptail = NULL;
	pq->size = 0;
}
void QueueDestroy(Queue* pq)
{
	assert(pq);
	QNode* p = pq->phead;
	while (p)
	{
		QNode* next = p->next;
		free(p);
		p = next;
	}

	pq->phead = pq->ptail = NULL;
	pq->size = 0;
}
bool QueueEmpty(Queue* pq)
{
	assert(pq);
	return pq->size == 0;
}
void QueuePush(Queue* pq, QDataType x)
{
	//如果是插入第一个元素，那么头指针和尾指针一样
	if (pq->phead==NULL)
	{
		pq->ptail = (QNode*)malloc(sizeof(QNode));
		pq->ptail->data = x;
		pq->ptail->next = NULL;
		pq->phead = pq->ptail;
	}
	else
	{
		QNode* temp = (QNode*)malloc(sizeof(QNode));
		temp->data = x;
		temp->next = NULL;
		pq->ptail->next = temp;
		//此时不能再将phead赋值成ptail，因为ptail是指向尾部的指针，phead是指向头部的指针，初始时赋值为ptail，此后ptail向后移动，phead的值保持不变以维持队列的头一直是第一个入队元素
		pq->ptail = temp;//重新指向尾部
	}
	pq->size++;
}
void QueuePop(Queue* pq)
{
	assert(pq);
	assert(!QueueEmpty(pq));
	//当只有一个节点时
	if (pq->phead->next== NULL)
	{
		free(pq->phead);
		pq->phead = pq->ptail = NULL;
		pq->size = 0;
	}
	else
	{
		QNode* temp = pq->phead->next;
		free(pq->phead);
		pq->phead = temp;
		pq->size--;
	}
}
QDataType QueueFront(Queue* pq)
{
	assert(pq);
	assert(!QueueEmpty(pq));
	return pq->phead->data;
}
QDataType QueueBack(Queue* pq)
{
	assert(pq);
	assert(!QueueEmpty(pq));
	return pq->ptail->data;
}
int QueueSize(Queue* pq)
{
	assert(pq);
	return pq->size;
}

class MyStack {
public:
    Queue _push;//用于入队
    Queue _pop;//用于出队
    MyStack() {
       QueueInit(&_push);//注意这个地方，用纯c写的话可能要写creat函数，那个直接用malloc MyStack即可，MyStack是个结构体，内部包含两个队列的变量
       QueueInit(&_pop);  
    }
    
    void push(int x) {
        QueuePush(&_push,x);
    }
    
    int pop() {
        //将前n-1个元素入pop队列中
        while(_push.size>1)
        {
            QueuePush(&_pop,QueueFront(&_push));
            QueuePop(&_push);
        }
        //第n个元素即为模拟栈的栈顶元素
        int result=QueueFront(&_push);
        QueuePop(&_push);
        while(_pop.size)
        {
            QueuePush(&_push,QueueFront(&_pop));
            QueuePop(&_pop);
        }
        return result;
    }
    
    int top() {
        while(_push.size>1)
        {
            QueuePush(&_pop,QueueFront(&_push));
            QueuePop(&_push);
        }
        int result=QueueFront(&_push);
        //注意别忘了彻底清空_push队列后再将_pop队列中的元素入队，还要记得将第n个元素加入到pop队列中
        QueuePush(&_pop,QueueFront(&_push));
        QueuePop(&_push);
        while(_pop.size)
        {
            QueuePush(&_push,QueueFront(&_pop));
            QueuePop(&_pop);
        }
        return result;
    }
    
    bool empty() {
       return QueueEmpty(&_push);
    }
};

3.4 没错，用栈实现队列

思路分析：

一样的，我们还是画图方便理解

代码实现：

typedef int STDataType;
typedef struct Stack
{
	STDataType* a;
	int top;//栈顶
	int capacity;//容量
}ST;
void STInit(ST* pst)
{
	assert(pst);//先断言一下，防止为空指针
	pst->a = NULL;
	pst->top = 0;//如果让top初始化为-1，那么就相当于top直接指向栈顶元素，这样不利于我们在空间已满时realloc空间的判断，所以我们选择初始时就让top指向栈顶元素的下一个元素(初始相当于栈顶下标为-1)
	pst->capacity = 0;
}

void STDestroy(ST* pst)
{
	assert(pst);
	free(pst->a);
	pst->a = NULL;//释放后不要忘记置空，防止其成为野指针
	pst->capacity = pst->top = 0;
}
bool STEmpty(ST* pst)
{
	assert(pst);
	return pst->top == 0;
}
void STPush(ST* pst, STDataType x)
{
	//先判断是否需要扩容
	if (pst->capacity == pst->top)
	{
		int newcapacity = 2 * pst->capacity + 10;//加上10的目的是为了防止pst->capacity=0的情况
		STDataType* temp = (STDataType*)realloc(pst->a,sizeof(int) * newcapacity);
		//如果开辟不成功
		if (!temp)
		{
			perror("开辟未成功\n");
			return;
		}
		pst->a = temp;
		pst->capacity = newcapacity;
	}
	pst->a[pst->top++] = x;
}


void STPop(ST* pst)
{
	assert(pst);
	//先判断是否为空
	assert(!STEmpty(pst));

	pst->top--;
}

STDataType STTop(ST* pst)
{
	assert(pst);
	//先判断是否为空
	assert(!STEmpty(pst));

	return pst->a[(pst->top) - 1];
}

int STSize(ST* pst)
{
	assert(pst);
	return pst->top;
}

class MyQueue {
public:
    ST _push;
    ST _pop;
    MyQueue() {//初始化
        STInit(&_push);
        STInit(&_pop); 
    }
    
    void push(int x) {
       STPush(&_push,x);
    }
    
    int pop() {
       while(!STEmpty(&_push))
       {
           STPush(&_pop,STTop(&_push));
           STPop(&_push);
       }
       int result=STTop(&_pop);
       //别忘了清除_pop栈的栈顶元素再倒回到_push栈
       STPop(&_pop);
       while(!STEmpty(&_pop))
       {
           STPush(&_push,STTop(&_pop));
           STPop(&_pop);
       }
       return result;
    }
    
    int peek() {
      while(!STEmpty(&_push))
       {
           STPush(&_pop,STTop(&_push));
           STPop(&_push);
       }
       int result=STTop(&_pop);
       //这个不能删除栈顶元素
       //STPop(&_pop);
       while(!STEmpty(&_pop))
       {
           STPush(&_push,STTop(&_pop));
           STPop(&_pop);
       }
       return result;
    }
    
    bool empty() {
       return STEmpty(&_push);
    }
};

3.5 设计循环队列

思路分析：

这个题，我们就不能再简单的套用模板队列了，我们需要用到环形队列来实现：

而我们一般会选用数组来实现环形队列，原因如下：

1.操作简单：因为数组的元素在内存中是连续存储的，所以读取和修改元素的操作非常简单和高效，适合用于实现队列等需要频繁读取和修改元素的数据结构。

2.实现方便：环形队列的实现中需要对队列的容量进行限制，而使用数组实现，可以很轻松地存储和修改队列的容量，扩展起来方便。

我们来用图理解环形队列及其存储原理,顺便把实现过程中的部分策略给出(其实我是懒得写了~~~）

 基于上述的说明，我们给出代码，注意很多地方存在取模操作，不难理解但是可能会考虑不到.

代码实现：

typedef struct {
    int front;
    int rear;
    int size;//表示循环队列的容量
    int *a;
} MyCircularQueue;


MyCircularQueue* myCircularQueueCreate(int k) {
    MyCircularQueue* obj=(MyCircularQueue*)malloc(sizeof(MyCircularQueue));
   //注意要进行两次malloc操作
   obj->a=(int*)malloc(sizeof(int)*(k+1));//多开一个空间，方便表示队列已满
   obj->front=obj->rear=0;
   obj->size=k;
   return obj;
}
bool myCircularQueueIsEmpty(MyCircularQueue* obj) {
     return obj->front==obj->rear;
}

bool myCircularQueueIsFull(MyCircularQueue* obj) {
     return (obj->rear+1)%(obj->size+1)==obj->front;//这个的地方需要注意
}

bool myCircularQueueEnQueue(MyCircularQueue* obj, int value) {
     if(!myCircularQueueIsFull(obj))//如果不满
     {
         obj->a[obj->rear]=value;
         obj->rear++;
         obj->rear%=(obj->size+1);
     }
     else
         return false;
     return true;
}

bool myCircularQueueDeQueue(MyCircularQueue* obj) {
     
     if(!myCircularQueueIsEmpty(obj))//如果非空
     {
        obj->front++;
        obj->front%=(obj->size+1);
     }
     else
        return false;
     return true;
}

int myCircularQueueFront(MyCircularQueue* obj) {
    if(!myCircularQueueIsEmpty(obj))
    {
        return obj->a[obj->front];
    }
    return -1;
}

int myCircularQueueRear(MyCircularQueue* obj) {
    if(!myCircularQueueIsEmpty(obj))
    {
        return obj->a[(obj->rear-1 + obj->size+1)%(obj->size+1)];
    }
    return -1;
}


void myCircularQueueFree(MyCircularQueue* obj) {
    free(obj->a);
    obj->a=NULL;
    obj->front=obj->rear=obj->size=0;
    free(obj);
    obj=NULL;

}

总结：

       栈和队列实际上还存在着许多的应用场景，较多的还是对STL中的栈和队列的使用，比如迷宫问题，广度优先搜索问题等等，包括还有很多的优化结构，用于实现某些特定的算法，如单调栈，单调队列，双端队列，优先队列等等，后续我也会继续更新数据结构相关的知识,目前也是正在筹备单调栈和单调队列，也希望可以更好的帮助到大家。

4.金句频道

       怕文章太长了你们看的烦了，我就少啰嗦一两句，都是我平时在网上看到的，颇有感触的文案，希望可以在忙碌的生活中，治愈我们大家。

        世界上什么都不公平，唯独时间是公平的。把时间拿来多读点书，多挣点钱，少去想那些没用的，努力不是为了得到更多，而是为了有更多的选择，为了当好运降临到自己身上时，你会觉得“我配”，而不是看着好事降临到别人身上时的“我呸”。

 

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/533446.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

PMP考试100个主要知识点

PMP考试100个主要知识点

1.一个项目在启动阶段会进行量级估算&#xff0c;准确范围是-50至100%。2000版的量级估算准确度为&#xff1a;-25%到75%。 2.质量控制通常先于范围确认执行&#xff0c;但这两个过程可以并列进行参考 3.Cost-plus-fixed-fee(CPFF)成本加固定费用合同。成本补偿型合同包括成本加…
阅读更多...
快速入门ChatGPT和AIGC：底层原理、热门工具、行业现状【我们能做什么】

快速入门ChatGPT和AIGC：底层原理、热门工具、行业现状【我们能做什么】

最近大家热议的ChatGPT和AI绘画工具的底层技术原理是什么&#xff1f;是如何发展到现在的&#xff1f;有哪些应用场景、热门工具&#xff1f;AIGC产业上下游有哪些公司&#xff1f;作为普通用户&#xff0c;我们还能接触哪些应用AI技术打造的商业解决方案&#xff1f;…… 我们…
阅读更多...
微信小程序 录音+播放组件封装

微信小程序 录音+播放组件封装

展示 长按录音 松开结束录音 点击播放 再次点击暂停 再次点击继续播放 展示效果&#xff1a; 录音功能 录音功能&#xff08;手指按下开始录音 手指松开结束录音&#xff09;&#xff1a; 使用wx原生录音功能在 component 外新建 wx.getRecorderManager() RecorderManager…
阅读更多...
国巨 ：硬件设计基础60条

国巨 ：硬件设计基础60条

硬件设计是现代科技发展中至关重要的领域之一。它涵盖了从微电子器件到复杂的系统级设计的各个方面&#xff0c;是现代电子产品的核心。在这篇文章中&#xff0c;我将介绍60个基础概念&#xff0c;这些概念是硬件设计工程师必备的知识&#xff0c;并且是设计出高质量硬件的关键…
阅读更多...
【web】学习ajax和fetch

【web】学习ajax和fetch

1/什么是ajax ajax 全名 async javascript and XML(异步JavaScript和XML) 是前后台交互的能⼒。 也就是我们客户端给服务端发送消息的⼯具&#xff0c;以及接受响应的⼯具。 在不重新加载整个网页的情况下&#xff0c;对网页的某部分进行更新。而传统的网页(不使用 Ajax)如果需…
阅读更多...
设计师必备的5个素材库，马住

设计师必备的5个素材库，马住

今天就告诉大家设计师都是去哪些网站找素材&#xff0c;分享五个网站&#xff0c;解决你80%的设计素材&#xff0c;建议收藏&#xff01; 1、菜鸟图库 https://www.sucai999.com/?vNTYxMjky 这是一个为新手设计师提供免费素材的设计网站&#xff0c;站内有超多平面模板、海报…
阅读更多...
成为一名黑客需要学什么

成为一名黑客需要学什么

想成为一名专业黑客&#xff0c;但不知道从哪里学起”很多人向盾叔问过这个问题&#xff0c;今天盾叔就为你介绍成为专业黑客必须学习的十个方面的知识&#xff0c;希望能为迷惘中的你指明方向。 一、基本的计算机知识 把它列为第一条&#xff0c;相信很多人肯定会觉得不以为…
阅读更多...
Java虚拟机快速入门 | JVM引言、JVM内存结构、直接内存

Java虚拟机快速入门 | JVM引言、JVM内存结构、直接内存

目录 一&#xff1a;JVM引言 1. 什么是 JVM ? 2. 常见的 JVM 3. 学习路线 二&#xff1a;JVM内存结构 1. 程 序 计 数 器&#xff08;PC Register&#xff09; 2. 虚 拟 机 栈&#xff08;JVM Stacks&#xff09; 3. 本 地 方 法 栈&#xff08;Native Method Stacks&…
阅读更多...
Vscode C++环境配置

Vscode C++环境配置

多文件编译 打开设置搜索coderunner 找到Executor Map 加入-I目录名 目录名/*.cpp 调试 点击调试以后会产生tasks.json文件&#xff0c;加入链接文件和库文件
阅读更多...
map用法以及特殊值的情况

map用法以及特殊值的情况

map用法以及特殊值的情况 一、map用法的说明 map(callbackFn, thisArg); // callbackFn回调函数&#xff0c;thisArg可选 callbackFn是个回调函数&#xff0c;该回调函数的参数按照顺序为element&#xff08;当前正在处理的元素&#xff09;&#xff0c;index&#xff08;正…
阅读更多...
WPF MaterialDesign 初学项目实战（1）首页搭建

WPF MaterialDesign 初学项目实战（1）首页搭建

前言 最近在学WPF&#xff0c;由于人比较烂&#xff0c;有一个星期没怎么动代码了。感觉有点堕落。现在开始记录WPF项目&#xff0c;使用MaterialDesignInXamlToolkit。 环境搭建 如果没下载MaterialDesign 的源码 github源码运行 在Nuget里面引入MaterialDesign Materia…
阅读更多...
数字孪生技术在环境保护领域怎样应用？

数字孪生技术在环境保护领域怎样应用？

近年来&#xff0c;环境保护成为全球范围内的热点话题&#xff0c;各国都在积极探索创新的解决方案。其中&#xff0c;数字孪生技术的出现为环境保护带来了全新的机遇和挑战。数字孪生技术将物理世界与数字世界相结合&#xff0c;通过精确的模拟和实时数据分析&#xff0c;为环…
阅读更多...
华为ensp 防火墙的基础配置

华为ensp 防火墙的基础配置

拓扑图&#xff1a; [FW3-zone-isp1]set priority 12 #配置防火墙优先级 步骤一 #首先进入防火墙需要输入默认账号和密码&#xff0c;必须修改密码。 [USG6000V1] undo in en #关闭提示。 #先配置ip。 [USG6000V1]ip route-static 0.0.0.0 0.0.0.0 64.1.1.10 #配置去往外网的默…
阅读更多...
【Redis】Redisson入门以及Redisson可重入锁的lua脚本实现

【Redis】Redisson入门以及Redisson可重入锁的lua脚本实现

目录 一、Redisson介绍 二、Redisson的入门 1、引入依赖 2、配置客户端 3、使用锁 三、Redisson可重入锁的原理 1、原理 2、实现 3、lua脚本保证原子性 1.获取锁 2.释放锁 一、Redisson介绍 在之前的文章里我们通过redis中的setn实现了一个简单的分布式锁以及解决了…
阅读更多...
远程协助软件推荐，有哪些远程协助工具？

远程协助软件推荐，有哪些远程协助工具？

Win10、11自带远程协助工具-快速助手 Win10、11的快速助手使用非常简单。只要在左下角的搜索框搜索一下就可以找到了。 我们都知道&#xff0c;Windows带有远程桌面RDP功能&#xff0c;而快速助手是通过Windows的远程连接机制实现的。所以在使用前&#xff0c;被控端需要开启系…
阅读更多...
谈薪谈蹦了，阿里HR说我不配21K....

谈薪谈蹦了，阿里HR说我不配21K....

好家伙&#xff0c;这奇葩事可真是多&#xff0c;前两天和粉丝聊天&#xff0c;他说前段时间面试阿里的测开岗&#xff0c;最后和面试官干起来了。 我问他为什么&#xff0c;他说没啥&#xff0c;就觉得面试官太装了&#xff0c;我说要24K&#xff0c;他说太高了&#xff0c;说…
阅读更多...
Kyligence Zen 产品体验——超好用指标平台一站式体验教程

Kyligence Zen 产品体验——超好用指标平台一站式体验教程

目录 背景介绍Kyligence Zen介绍上手指南数据概览可视化图表 自定义数据新建表新建视图 指标体验目标仪表盘集成优点个人建议体验总结每文一语 背景介绍 在数字化建设初期&#xff0c;许多企业主要采用基于商业智能&#xff08;BI&#xff09;报表的方式来处理数据&#xff0c…
阅读更多...
杨红春没有“雷军”，良品铺子“高端”之路焦虑

杨红春没有“雷军”，良品铺子“高端”之路焦虑

文 | 螳螂观察 作者 | 图霖 如果休闲零食赛道要评一个六边形战士&#xff0c;良品铺子绝对是个不错的候选人。 尽管搭乘电商的风头起势&#xff0c;但得益于早期线下开店的经验&#xff0c;成功实现了两条腿走路。最新年报显示&#xff0c;其2022年线上收入占比为50.42%&…
阅读更多...
《统计学习方法》——隐马尔可夫模型(上)

《统计学习方法》——隐马尔可夫模型(上)

引言 隐马尔可夫模型(Hidden Markov Model,HMM)是描述隐藏的马尔可夫链随机生成观测数据过程的模型。 前置知识 马尔可夫链 马尔可夫链(Markov chain)又称离散时间马尔可夫链&#xff0c;使用 t t t来表示时刻&#xff0c;用 X t X_t Xt​来表示在时刻 t t t链的状态&#…
阅读更多...
( 位运算 ) 338. 比特位计数 ——【Leetcode每日一题】

( 位运算 ) 338. 比特位计数 ——【Leetcode每日一题】

❓338. 比特位计数 难度&#xff1a;简单 给你一个整数 n &#xff0c;对于 0 < i < n 中的每个 i &#xff0c;计算其二进制表示中 1 的个数 &#xff0c;返回一个长度为 n 1 的数组 ans 作为答案。 示例 1&#xff1a; 输入&#xff1a;n 2 输出&#xff1a;[0,1,…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023