❓338. 比特位计数

难度：简单

给你一个整数 n ，对于 0 <= i <= n 中的每个 i ，计算其二进制表示中 1 的个数 ，返回一个长度为 n + 1 的数组 ans 作为答案。

示例 1：

输入：n = 2
输出：[0,1,1]
解释：
0 --> 0
1 --> 1
2 --> 10

示例 2：

输入：n = 5
输出：[0,1,1,2,1,2]
解释：
0 --> 0
1 --> 1
2 --> 10
3 --> 11
4 --> 100
5 --> 101

提示：

• $0<=n<=10^5$

进阶：

• 很容易就能实现时间复杂度为 $O(nlogn)$ 的解决方案，你可以在线性时间复杂度 $O(n)$ 内用一趟扫描解决此问题吗？
• 你能不使用任何内置函数解决此问题吗？（如，C++ 中的 __builtin_popcount ）

💡思路：位运算

基础知识必知：一篇文章搞懂位运算 !

对于数字 6(110)，它可以看成是 4(100) 再加一个 2(10)，因此 dp[i] = dp[i&(i-1)] + 1;

即，使用位运算 去除最低的那一位 1，此时的 dp[i&(i-1)] 的已经计算过，然后再加上最低为的这个 1。

🍁代码：(Java、C++)

Java

class Solution {
    public int[] countBits(int n) {
        int[] ans = new int[n + 1];
        for(int i = 1; i <= n; i++){
            ans[i] = ans[i & (i - 1)] + 1;
        }
        return ans;
    }
}

C++

class Solution {
public:
    vector<int> countBits(int n) {
        vector<int> ans(n + 1);
        for(int i = 1; i <= n; i++){
            ans[i] = ans[i & (i - 1)] + 1;
        }
        return ans;
    }
};

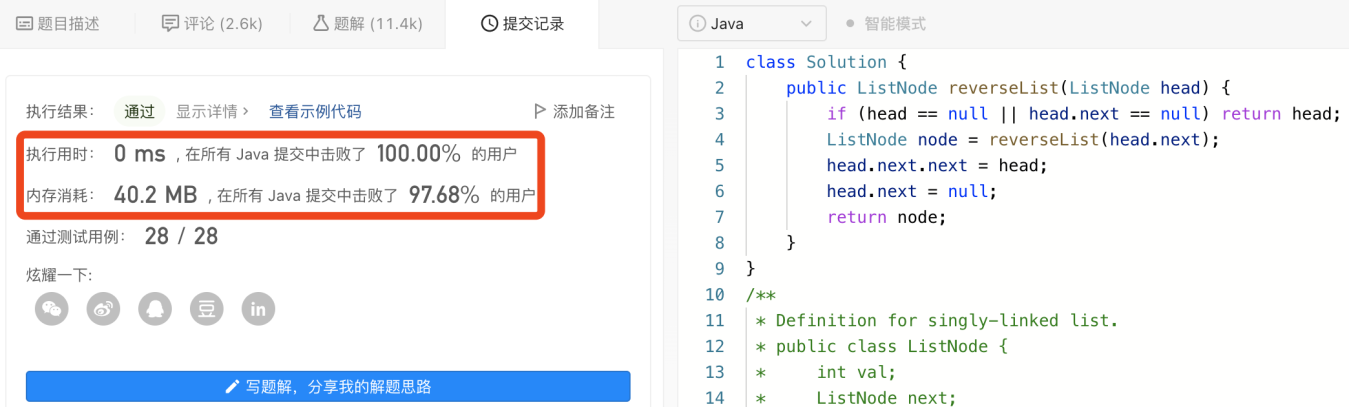
🚀 运行结果：

🕔 复杂度分析：

• 时间复杂度：$O(n)$，对于每个整数，只需要 $O(1)$ 的时间计算「一比特数」。
• 空间复杂度：$O(n)$，除了返回的数组以外，空间复杂度为常数。

题目来源：力扣。

放弃一件事很容易，每天能坚持一件事一定很酷，一起每日一题吧！
关注我 leetCode专栏，每日更新！

注： 如有不足，欢迎指正！