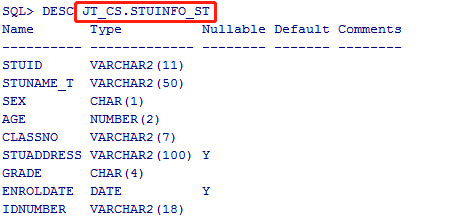
并查集这个数据结构本身并不难,其主要是提供一个思路,方便我们编写图的代码,和一些OJ题
文章目录
- 1.什么是并查集?
- 2.思路
- 2.1 合并集合
- 2.2 压缩路径
- 3.代码
- 4.OJ题
- 4.1 剑指 Offer II 116. 省份数量
- 4.2 等式方程的可满足性
1.什么是并查集?
并查集是多个独立集合的合集,用于表示数据之间的关系。
比较生动的例子,就是我们生活中的朋友圈(不是wx的那个啊)
- 张三和李四是好朋友,那么他们就构成了一个集合A
- 王舞和王陆是好朋友,那么他们也构成了一个集合B
- 此时,王舞突然认识了李四,这时候,就可以把A和B合并成一个集合
推而广之,一个并查集中可以有多个这样的集合,多个朋友圈。
- 并查集中的每一个集合是用多叉树来表示的
2.思路
并查集的思路并不难,给定一个数组的大小(需要在另外的地方管理编号)创建一个并查集
下标即为数据的编号
- 设定元素的初始值都是-1
- 如果下标1和3为一个集和,那就把3的元素(初始值-1)加到1处,即1的元素为-2;再把3的元素设置为1的下标,即3的元素为1
- 依此类推,最终只要下标所对应元素不为负数,那么这个下标就是一个集和的成员
- 如果为负数,那么就是一个集合的根,且元素为这个集和中成员的个数(绝对值)
如图所示,下标678所对应元素为0,代表它们属于以下标0为根的一个集合。而下标0处的元素为-4,代表这个集合里面有4个元素
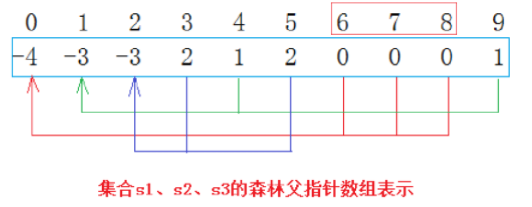
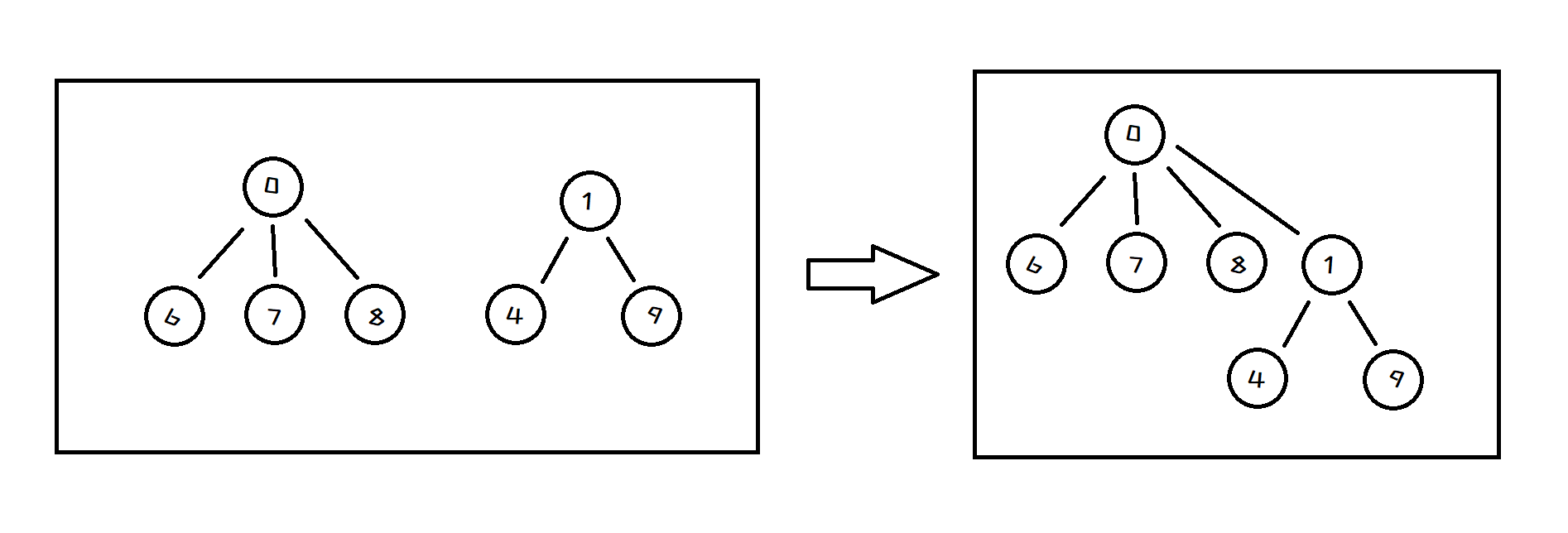
2.1 合并集合
如果我们需要合并一个集合,以上图中的0集合和1集合为例。我们只需要将1集合的元素-3加到0集合上,再把1集合的元素改成0即可
此时的树就会是这样的👇
2.2 压缩路径
当节点很多,集合可能会出现路径长度过大的情况。这时候我们就需要进行路径的压缩
其方法很简单。遍历整个并查集,将同一集合的子节点改成相同的父亲即可
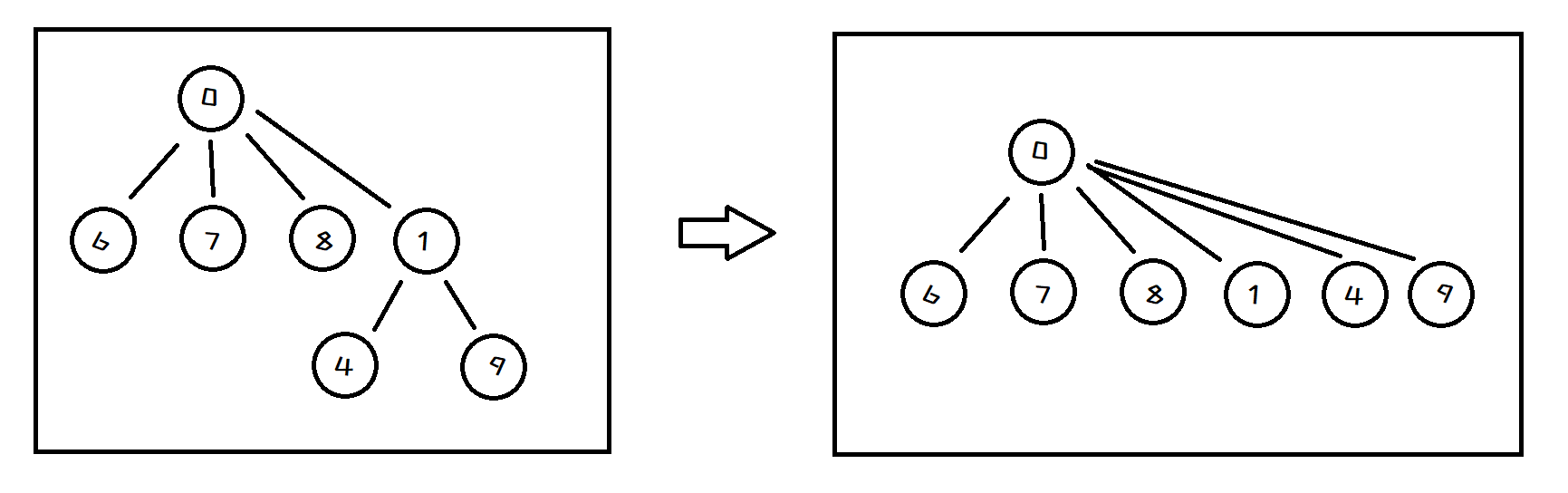
这样在向上找集合的根时,无须跳转多次,一次就能找到。
但由于并查集的访问是依靠数组下标实现的随机访问,时间复杂度为O(1),只有数据样本量极大的时候,这么做才能有效果
3.代码
相比于其他数据结构复杂的实现,并查集的实现就简单多了。主要的函数只有几个,可以通过封装vector来实现
class UnionFindSet {
public:
UnionFindSet(const int sz)
:_set(sz,-1)//调用vector构造函数,初始化sz个-1
{}
void Union(int x, int y)//设置x和y为一个集合
{
int r1 = FindRoot(x);
int r2 = FindRoot(y);
if (r1 != r2)//不在一个集和中
{
_set[r1] += _set[r2];
_set[r2] = r1;
}
}
int FindRoot(int n)//找这个集合的根
{
while (_set[n] >= 0)
{
n = _set[n];
}
return n;//负数的时候为根
}
bool isUnion(int x,int y)//判断是否在一个集合中
{
return FindRoot(x) == FindRoot(y);
}
int UnionSZ()//返回有几个集合
{
int count = 0;
for (int i = 0; i < _set.size(); i++)
{
if (_set[i] < 0)
{
count++;
}
}
return count;
}
private:
vector<int> _set;//用来存放对应关系
};
这里没有写压缩路径的代码,其实也就是一个遍历搞定的事😂
4.OJ题
4.1 剑指 Offer II 116. 省份数量
剑指 Offer II 116. 省份数量

有了并查集,这道题就非常简单。最重要的是思路。我们无须现场造一个轮子,只需要写好找根函数,用一个数组就能实现一个简单的并查集
class Solution {
public:
int FindRoot(const vector<int>& v,int n)
{
int prev = n;//初始下标
while(v[prev]>=0)//它的父亲下标
{
prev=v[prev];//如果不为负数,那就还是需要往前找
}
return prev;
}
int findCircleNum(vector<vector<int>>& isConnected)
{
vector<int> v(isConnected.size(),-1);
for(int i=0;i<isConnected.size();i++)
{
for(int j=0;j<isConnected[i].size();j++)
{
if(isConnected[i][j]==1)//为1代表是一个集合中的元素
{
int root1 = FindRoot(v,i);
int root2 = FindRoot(v,j);
if(root1!=root2)
{
v[root1] += v[root2];
v[root2] = root1;
}
}
}
}
int count = 0;
for(int i=0;i<v.size();i++)
{
if(v[i]<0)
{
count++;
}
}
return count;
}
};
4.2 等式方程的可满足性
990.等式方程的可满足性
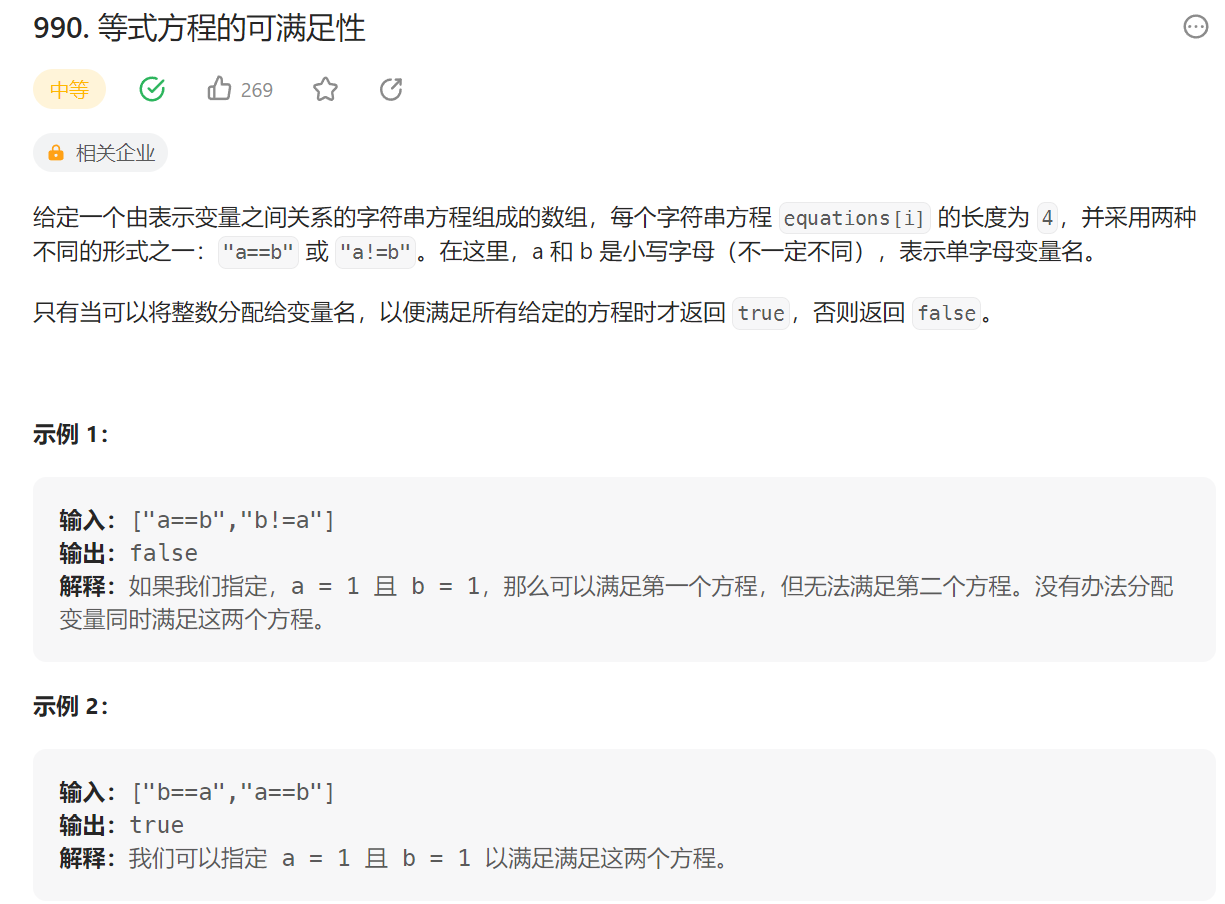
这道题和上面那一道差不多,只不过把省份换成了字母之间的关系
class Solution {
public:
int FindRoot(const vector<int>& v,int n)
{
int prev = n;//初始下标
while(v[prev]>=0)//它的父亲下标
{
prev=v[prev];//如果不为负数,那就还是需要往前找
}
return prev;
}
bool equationsPossible(vector<string>& equations) {
vector<int> v(26,-1);//因为题目给的都是小写字母,直接建立26个小写字母的映射表
for(int i=0;i<equations.size();i++)
{
int root1 = FindRoot(v,equations[i][0]-'a');//第一个字母
int root2 = FindRoot(v,equations[i][3]-'a');//第二个字母
if(equations[i][1]=='=')//代表等于
{
if(root1!=root2)
{//设置为一个集合中的元素
v[root1] += v[root2];
v[root2] = root1;
}
}
else//不等于
{
if(root1==root2)
{
//如果不等于的同时,根还相同
//说明是同一个集合,不符合题意
return false;
}
}
}
//还需要遍历第二遍,避免漏网之鱼
for(int i=0;i<equations.size();i++)
{
int root1 = FindRoot(v,equations[i][0]-'a');//第一个字母
int root2 = FindRoot(v,equations[i][3]-'a');//第二个字母
if(equations[i][1]=='!')//不等于
{
if(root1==root2)
{
//如果不等于的同时,根还相同
//说明是同一个集合,不符合题意
return false;
}
}
}
return true;
}
};