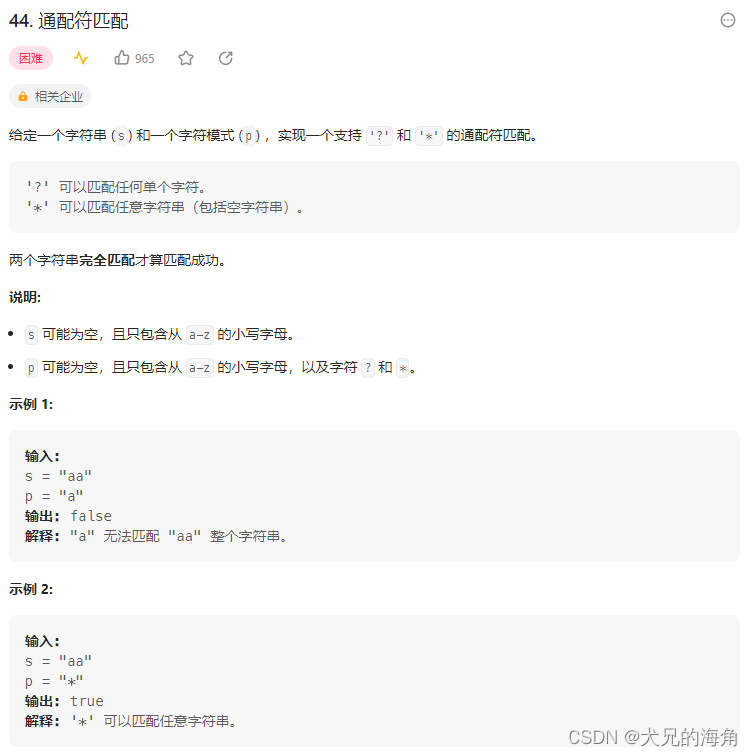
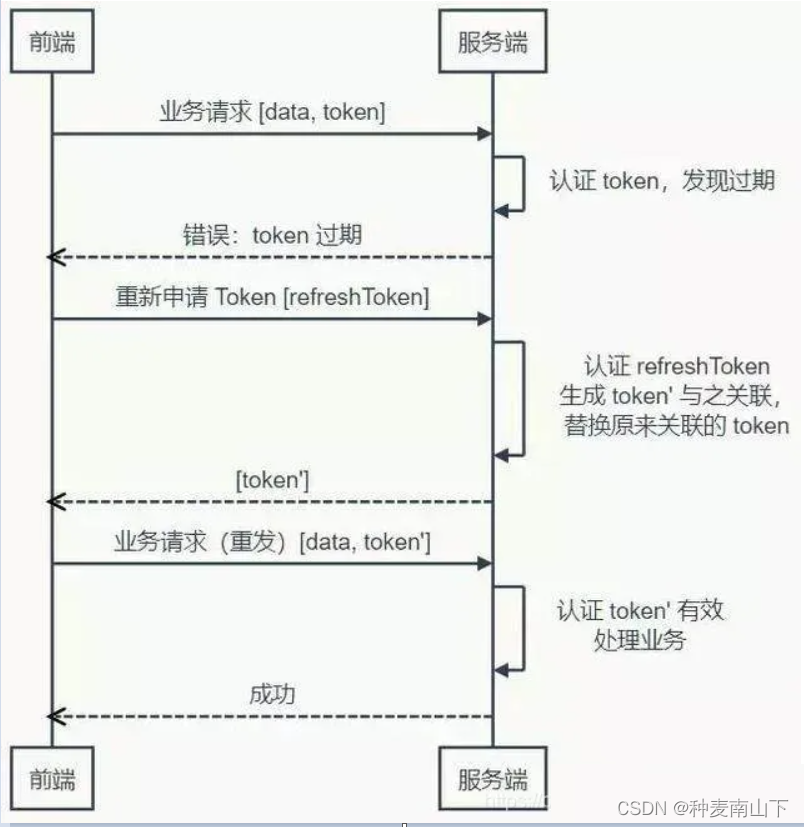
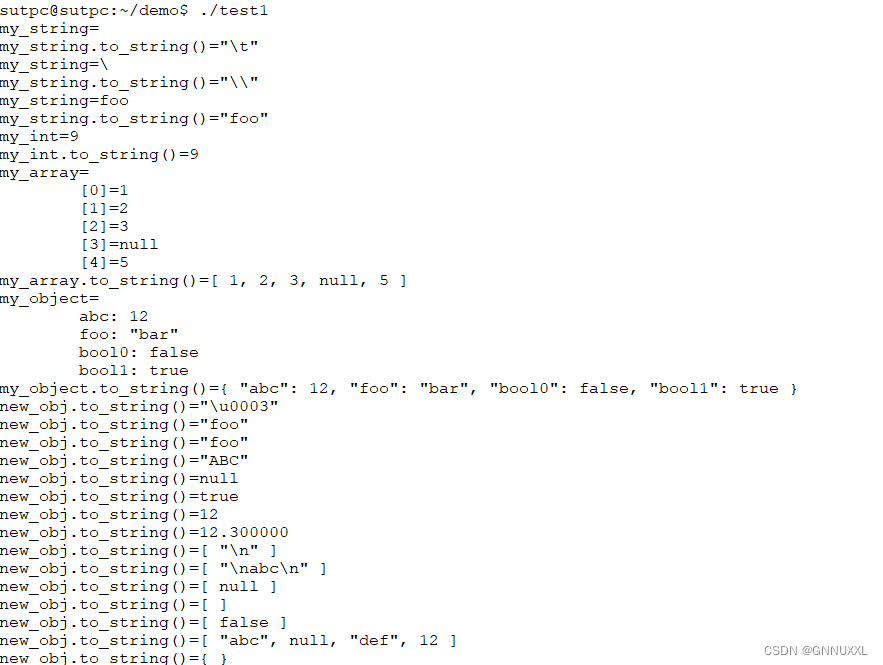
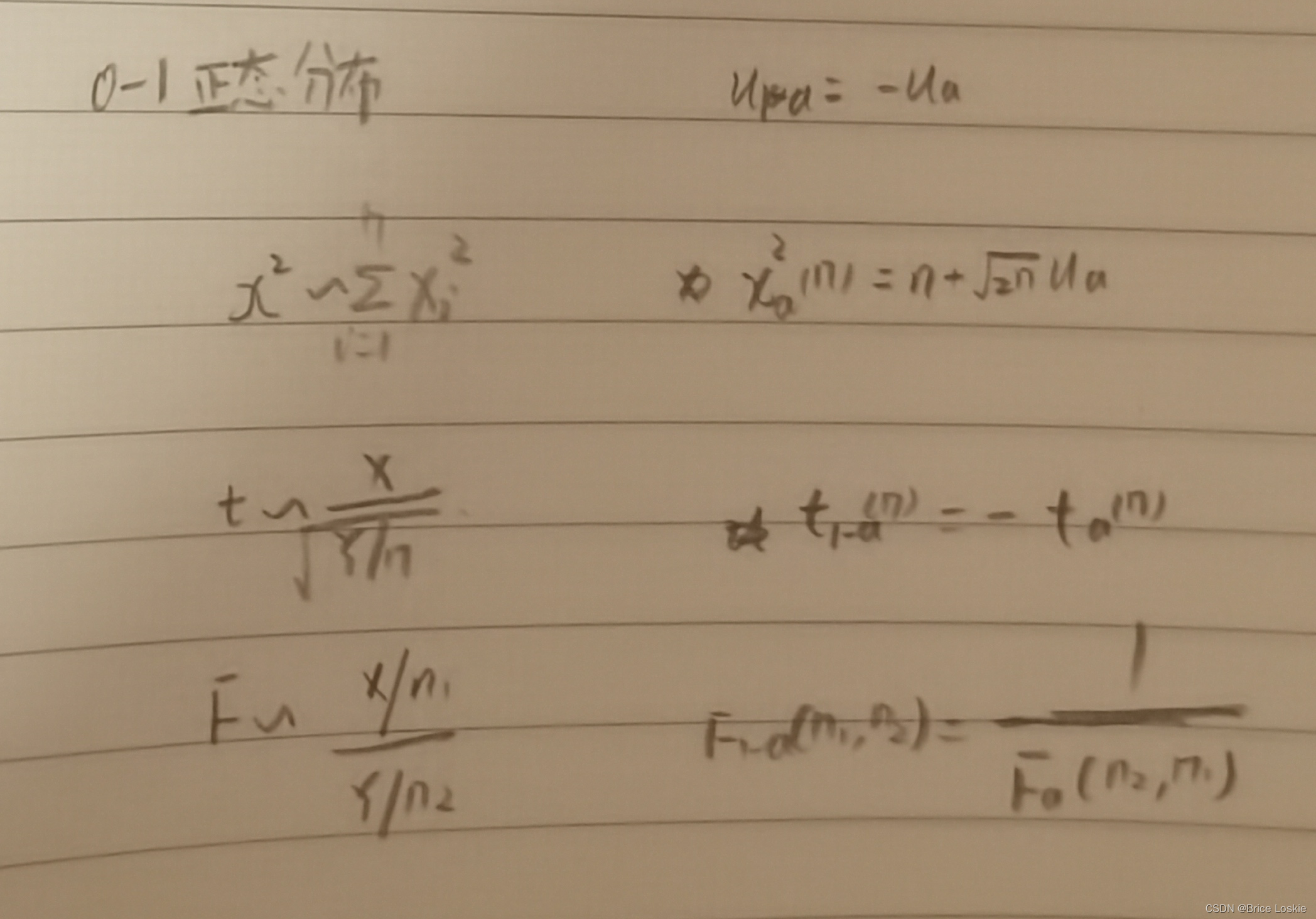本节介绍在数理统计中常用的几个基本分布。为此,先引进分位数定义。
定义1. 2. 1 设X为随机变量,则称满足
![]()
的为X的上侧
分位数,简称为(上侧)分位数.
1 标准正态分布
标准正态分布N (0,1)是构造其他分布的基础,其密度函数为
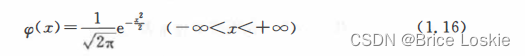
它的图形关于y轴对称(图1.1).
本书附表3给出了标准正态分布函数的取值情况. 对于数,通过查表,可求出满足等式
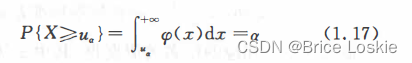
的上侧分位数(显然
),当
时,可查得
2.卡方分布
定理1. 2. 1 设是独立同分布的随机变量,且都服从标准正态分布
,则他们的平方和
(1. 18)
的分布密度是
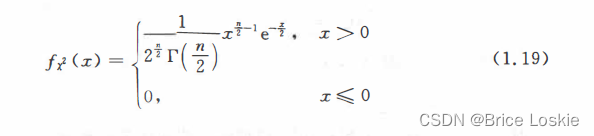
其中为伽马函数在
处的值.这种分布称为自由度为 n 的
分布,记作
根据定义(1. 18),我们容易求得分布的期望和方差分别为
![]()
事实上,我们有
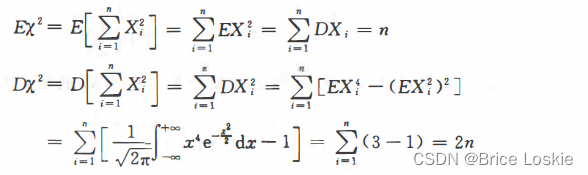
利用卷积公式,我们还可以证明分布具有下面的性质(见习题1. 3).
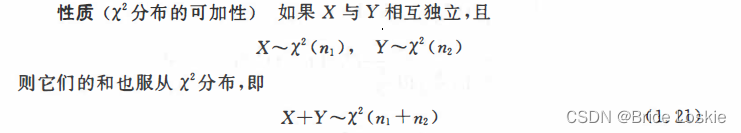
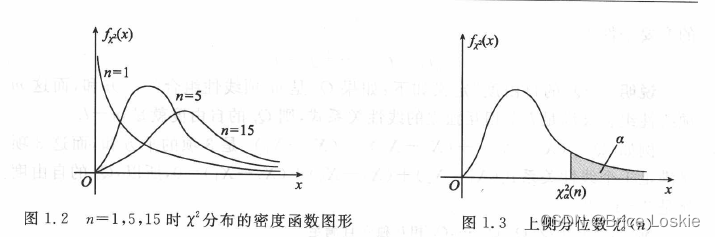
图1. 2 给出了n= 1,5,15 时x 2分布的密度曲线
本书附表5 中,对不同的n 及a(0<a<1),给出了满足等式
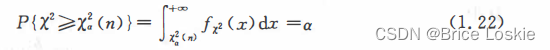
的上侧分位数图1. 3)
例如,当n=10,时,可以查得
当n较大(一般要求n>45)时,我们有近似计算公式
![]()
事实上,由X 2 的定义(1. 18)及中心极限定理知

因此,当n较大时,
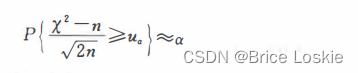
又因为
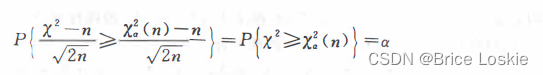
即式(1. 23) 成立
有了式(1. 23 ) ,我们就可以在n较大时,利用式(1. 23)近似计算分布的上
侧分位数值,如
![]()
3 t分布
定理1. 2. 3 设随机变量X与Y相互独立,且X服从标准正态分布N(0,1),Y服从自由度为n的卡方分布,则随机变量

这种分布称为自由度为n的t分布,记作T~t(n).
t分布的密度函数是偶函数,因此其密度曲线关于y轴对称
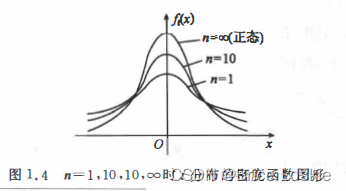
故当n很大时,t分布近似于正态分布N(0,1),但对千小的n,t分布与N(0,1)相差很大. 下图画出了n = 1,10, ∞时t分布的密度函数图形.
对不同的n及a(a=0.1,0.05,0. 025等),给出了满足等式
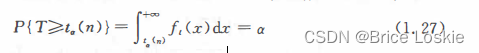
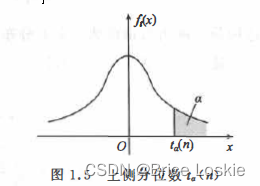
![]()
4.F分布


![]()
5.总结