本文主要简单介绍如何绘制混淆矩阵
首先混淆矩阵是机器学习中总结分类模型预测结果的情形分析表,以矩阵形式将数据集中的记录按照真实的类别与分类模型预测的类别判断两个标准进行汇总。
其实混淆矩阵就是用来判断我们的算法的分类准确度的一个可视化矩阵
1.使用matlab绘制混淆矩阵
可以使用函数 plotconfusion 来绘制混淆矩阵
plotconfusion(y_true, y_predict)其中y_true是我们一开始的分类的标签值,而y_predict使我们使用某个算法或者模型进行训练后对样本进行预测得到标签
注意:在使用函数前,要分别对二者使用categorical函数进行分类 如下:
predict_label = predict(SVMModel, data);
y_true = categorical(label);
y_predict = categorical(predict_label);
plotconfusion(y_true, y_predict)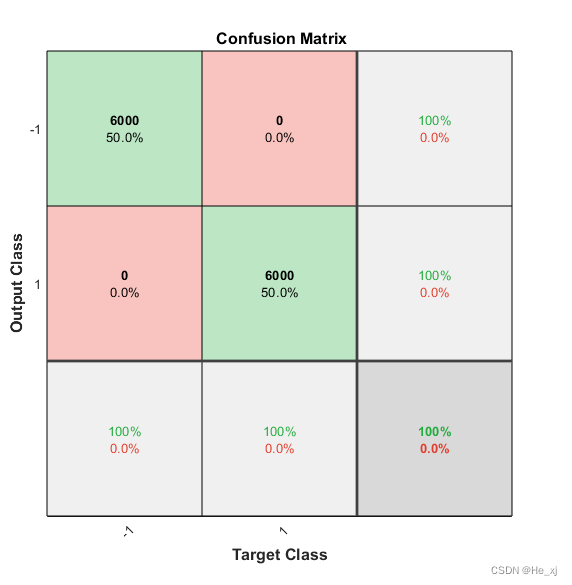
2.使用Python绘制混淆矩阵
使用sklearn库中的matrix中的confusion_matrix完成绘制
sklearn.metrics.confusion_matrix(y_true, y_pred, *, labels=None, sample_weight=None, normalize=None)from sklearn.metrics import confusion_matrix
import matplotlib.pyplot as plt
y_pred = [] # ['2','2','3','1','4'] # 类似的格式
y_true = [] # ['0','1','2','3','4'] # 类似的格式
# 对上面进行赋值
C = confusion_matrix(y_true, y_pred)
plt.matshow(C, cmap=plt.cm.Blues) # 根据最下面的图按自己需求更改颜色
for i in range(len(C)):
for j in range(len(C)):
plt.annotate(C[j, i], xy=(i, j), horizontalalignment='center', verticalalignment='center')
plt.ylabel('True label')
plt.xlabel('Predicted label')
plt.show()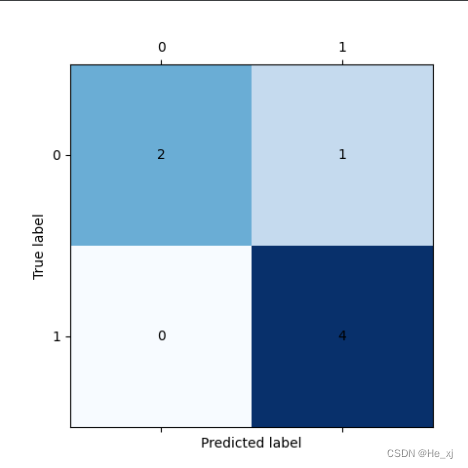
可见没有matlab绘制的图那么美观 ,当然你也可以深入研究如何使用python绘制更加精美的混淆矩阵图。
以上就是我分享的内容...