<~生~信~交~流~与~合~作~请~关~注~公~众~号@生信探索>

n 次伯努力事件(发生和不发生概率和为1)

发生r次的概率

期望： ，方差：

using Distributions
d=Binomial(4, 0.35);
mean(d) == 4*0.35
var(d) == 4*0.35(1-0.35)

Example

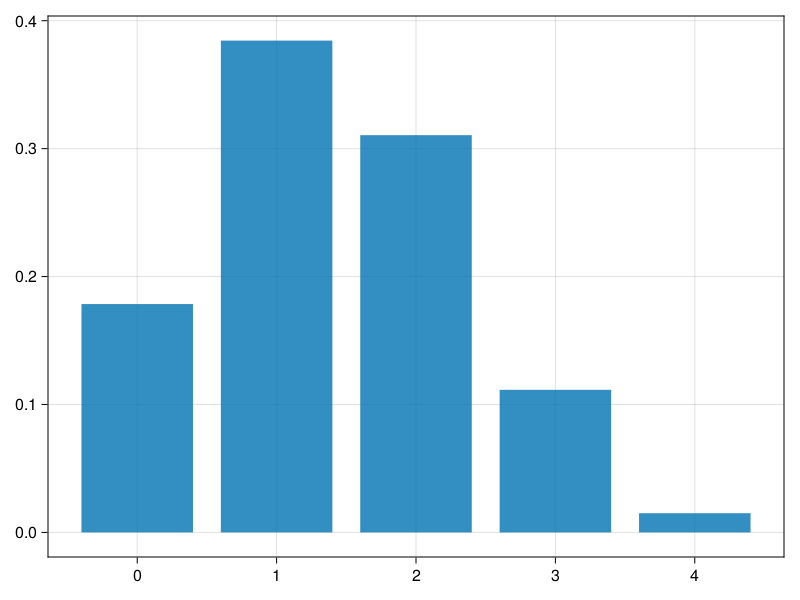
We asked various probability questions regarding the number of people out of 4 with blood type O+. We verified that the scenario was binomial and that each problem could be solved using the binomial formula. Instead of looking at it piecewise, we could describe the entire distribution of possible values and their corresponding probabilities. Since there are 4 people, there are several possible outcomes for the number who might have blood type O+: 0, 1, 2, 3, 4. We can make a distribution table with these outcomes. Recall that the probability of a randomly sampled person being blood type O+ is about 0.35.

pdf(distribution, x)计算分布密度（概率质量）函数在x处的值， 如果x是数组，结果返回数组； 如果x是数组且函数写成pdf!(distribution, x)，则结果保存在x中返回。 logpdf()计算其密度函数的自然对数值。

使用pdf实现发生0、1、2、3、4次的概率计算。

using CairoMakie,Distributions
CairoMakie.activate!()

let
    d=Binomial(4, 0.35);
    x = 0:4
    y = pdf.(d, x)
    barplot(x, y)
end

Mississippi问题

mississippi字母有多少种排列组合方式。

字母长度的阶乘除以s、i、p字母重复个数的阶乘，简单的例子是kis、kiss、kisss字母有多少种排列组合方式，可以使用枚举法、填空法求解。

using Combinatorics
multiset_permutations("mississippi",11) |> length == 34650
factorial(11)/(factorial(4)*factorial(4)*factorial(2)) == 34650.0

如果认为重复的字母是不一样的

permutations("mississippi") |> length == 39916800

Reference

https://www.bilibili.com/video/BV1CA411P7bL