线段树-哈工大数据结构与算法作业

news2024/10/6 0:28:50

title: 线段树-哈工大作业
date: 2023-05-16 11:42:26
tags: 数据结构与算法

  1. 线段树

问题：

区间查询求和问题:给定一个含有n个整数序列的数组A，查询任意区间最大值与区间和的复杂度为O(n)，若进行m次查询，则总的复杂度为O(mn)。

设计一个数据结构(线段树)，优化区间查询与求和操作，使其时间复杂度为O(logn)。举例描述说明:

1该数据结构的节点与结构;
2建立与更新（数组A中某一个元素值更新时）数据结构的具体步骤;
3任意区间查询与求和操作的具体步骤。

提示:更新数据结构时，采用延迟更新策略，即，更新时，不立即进行更新操作，只标记这个点需要更新，真正使用时（如查询时）才进行更新。

git地址：https://github.com/944613709/HIT-Data-Structures-and-Algorithms

举例说明：（代码在最后一起展示）

1、该数据结构的节点与结构;

1****结点：

typedef long long ll;

struct TREE

{

int l,r;//代表节点维护的区间范围;代表了a[l]->a[r] 

ll SUM; 代表了a[l]->a[r]的值的sum总和 

ll lazy; //涉及lazy标记的东西;

ll Max;//代表了a[l]->a[r]的值的最大值

}t[MAXN << 2];

L,r代表的是区间Data[l]->Data[r]

SUM代表的是这个区间的所有值的总和

Lazy标记用于采用延迟更新策略

Max代表的是这个区间的所有值的最大值

2****结构：

采用线段树来优化区间查询，每一个结点储存着Data[L]->Data[R]的信息，其中叶节点的L=R，不断地将大区间划分为小区间，利用递归建立线段树，

举例A【1】到A【6】的线段树

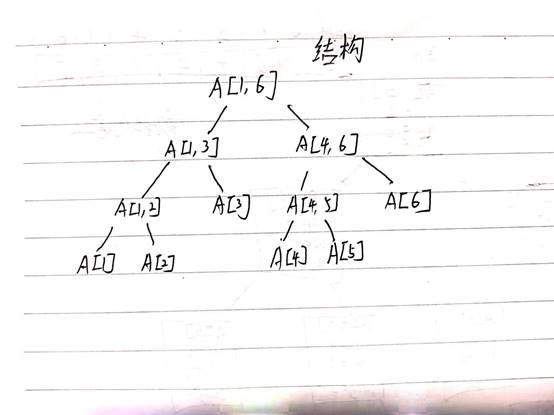
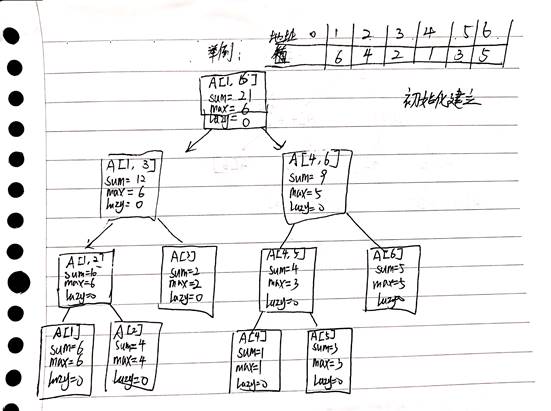
扫描全能王 2021-11-23 18.24_2扫描全能王 2021-11-23 18.24_3

2、建立与更新（数组A中某一个元素值更新时）数据结构的具体步骤;

建立：

若为叶子结点，直接赋值；否则根据构造左右子树得到该结点的值

1. 建立线段树

\1. 如果l == r情况则直接将SUM和Max 赋值为a[l]

\2. 如果l！=r情况，则递归建立线段树

(1) 定义Mid = t[p].l + t[p].r >> 1;

(2) 递归调用build(lson§,l,mid);处理左子树

(3) 递归调用build(rson§,mid + 1,r);处理右子树

(4) 回溯后将子节点信息保存下来t[p].SUM = t[lson§].SUM + t[rson§].SUM；t[p].Max = max(t[lson§].Max,t[rson§].Max);

举例A[1]=1,A[2]=2,A[3]=3,A[4]=4建立线段树

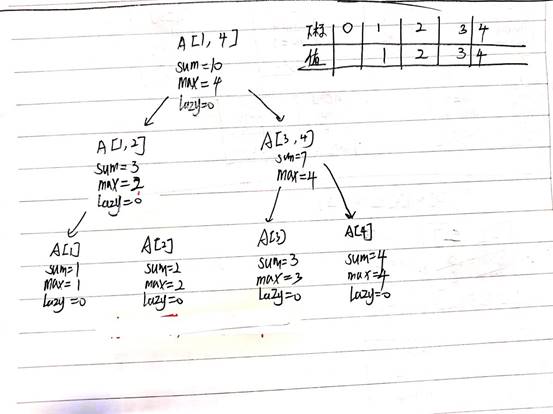
扫描全能王 2021-11-23 18.24_4

更新：

(1) 单个数值修改线段树（数组A中某一个元素值更新时），可以借助于已有的区间修改，不如想要将令A[L]的值变成y，利用区间更新函数等价于将从A[L]到A[L]的值都加入value =y-A[L]

而区间更新具体方法：

1、如果当前区间被完全覆盖在目标区间里，修改sum和max

2.如果没有完全覆盖，则先下传lazy

3、如果这个区间的左儿子和目标区间有交集，那么搜索左儿子

​ 4、如果这个区间的右儿子和目标区间有交集，那么搜索右儿子

\2. 区间更新线段树update函数

(1) 如果区间被覆盖的情况

① 直接进行修改

② t[p].SUM += value * (t[p].r - t[p].l + 1);

③ t[p].Max += value;

④ t[p].lazy += value;

⑤ Return结束

(2) 如果区间没有被覆盖的情况

① 执行push_down（p）函数，执行向下更新左右儿子结点的数据

\1) 当lazy不为零的时候，将左右儿子的值利用lazy修改左右儿子的SUM和Max

\2) 将当前p的lazy下传给左右儿子的lazy

\3) 当前p的lazy清零

② 定义mid = t[p].l + t[p].r >> 1便于后续判断

\1) 如果覆盖了左儿子就修改左儿子update(lson§,l,r,value)

\2) 如果覆盖了右儿子就修改右儿子update(rson§,l,r,value)

③ 更新当前p结点的Sum和Max数据

\3. 单个数值修改线段树（数组A中某一个元素值更新时）

(1) 令Data[L]的值变成y，利用区间更新函数等价于将Data[L]->Data[L]的值都加入value =y-Data[L]

(2) update(1,l,l,value);

举例：

更新A【1】修改为2（假定A[1]=1,A[2]=2,A[3]=3,A[4]=4建立线段树）****扫描全能王 2021-11-23 19.15_1

举例：

更新A【1】到A【3】的值都加入1（假定A[1]=1,A[2]=2,A[3]=3,A[4]=4建立线段树）

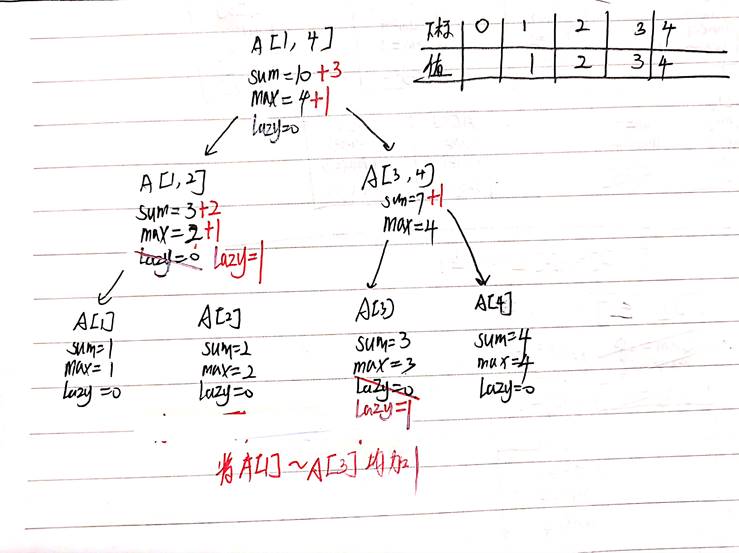
扫描全能王 2021-11-23 18.45_1

**3、**任意区间查询与求和操作的具体步骤。

1、如果当前区间被完全覆盖在目标区间里，直接return

2、如果没有完全覆盖，则先pushdown执行向下更新左右儿子结点的数据

3、如果这个区间的左儿子和目标区间有交集，那么处理左儿子

​ 4、如果这个区间的右儿子和目标区间有交集，那么处理右儿子

\4. 查询区间和querySum函数

(1) 如果区间被覆盖

① 直接返回区间的数据Returnt [p].SUM

(2) 如果区间没有被覆盖

① 执行push_down（P），执行向下更新左右儿子结点的数据

\1) 当lazy不为零的时候，将左右儿子的值利用lazy修改左右儿子的SUM和Max

\2) 将当前p的lazy下传给左右儿子的lazy

\3) 当前p的lazy清零

② 定义mid = t[p].l + t[p].r >> 1;方便后续判断

③ 如果(l <= mid)需要查询左儿子，就加入整理左儿子的数据sum += querySum(lson§,l,r)

④ 如果(r > mid)，如要查询右儿子，就加入整理右儿子的数据sum += querySum(rson§,l,r);

⑤ 返回return sum

\5. 查询区间最大值query_Max函数

(1) 如果区间被覆盖

① 直接return t[p].Max

(2) 如果区间没有被覆盖

① 定义mid = t[p].l + t[p].r >> 1;方便后续判定

② 定义maxL = -inf,maxR = -inf;

③ 如果(l <= mid)需要查询左儿子，则查左儿子的最大值maxL = max(maxL,query_Max(lson§,l,r));

④ 如果(r > mid)需要查询右儿子，则查询右儿子最大值maxR = max(maxR,query_Max(rson§,l,r));

(3) 返回 左右子树的最大值

举例：

查询A【2】到A【4】的区间和，最大值（假定，A[1]=1,A[2]=2,A[3]=3,A[4]=4建立线段树，并且已经更新A【1】到A【3】的值都加入1）

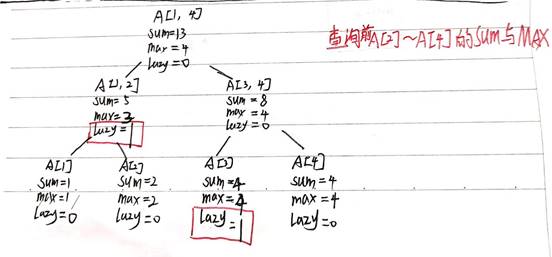
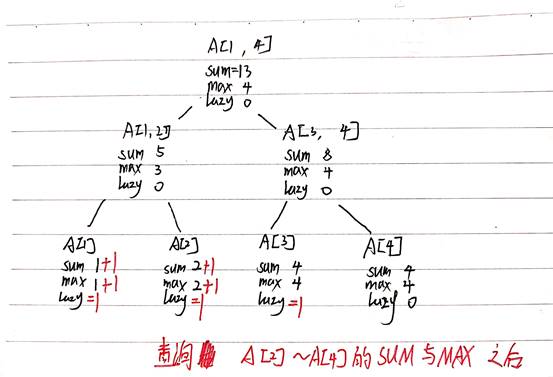
扫描全能王 2021-11-23 18.45_3扫描全能王 2021-11-23 18.45_4

得到查询结果

算法思想： 采用线段树来优化区间查询，每一个结点储存着Data[L]->Data[R]的信息，其中叶节点的L=R，不断地将大区间划分为小区间，利用递归建立线段树，在利用这些区间进行修改和查询。而在进行更新数据时候利用延迟标记lazy标记，如果当前区间需要被修改的区间被完全覆盖就用lazy标记，在下一次查询或者更新时候才调用lazy下传和清零修改

算法步骤

\6. 结点：

struct tree

{

int l,r;//代表节点维护的区间范围;代表了a[l]->a[r] 

ll SUM; //代表该节点维护的值;//!!!!!!!!!sum总和 

ll lazy; //涉及lazy标记的东西;

ll Max;//最大值

}t[MAXN << 2];

L,r代表的是区间Data[l]->Data[r]

SUM代表的是这个区间的所有值的总和

Lazy标记用于采用延迟更新策略

Max代表的是这个区间的所有值的最大值

ll Data[MAXN];，数组Data代表这每一个区间的一块地点存储的值

7. 建立线段树

\3. 如果l == r情况则直接将SUM和Max 赋值为a[l]

\4. 如果l！=r情况，则递归建立线段树

(1) 定义Mid = t[p].l + t[p].r >> 1;

(2) 递归调用build(lson§,l,mid);处理左子树

(3) 递归调用build(rson§,mid + 1,r);处理右子树

(4) 回溯后将子节点信息保存下来t[p].SUM = t[lson§].SUM + t[rson§].SUM；t[p].Max = max(t[lson§].Max,t[rson§].Max);

\8. 区间更新线段树update函数

(1) 如果区间被覆盖的情况

① 直接进行修改

② t[p].SUM += value * (t[p].r - t[p].l + 1);

③ t[p].Max += value;

④ t[p].lazy += value;

⑤ Return结束

(2) 如果区间没有被覆盖的情况

① 执行push_down（p）函数，执行向下更新左右儿子结点的数据

\1) 当lazy不为零的时候，将左右儿子的值利用lazy修改左右儿子的SUM和Max

\2) 将当前p的lazy下传给左右儿子的lazy

\3) 当前p的lazy清零

② 定义mid = t[p].l + t[p].r >> 1便于后续判断

\1) 如果覆盖了左儿子就修改左儿子update(lson§,l,r,value)

\2) 如果覆盖了右儿子就修改右儿子update(rson§,l,r,value)

③ 更新当前p结点的Sum和Max数据

\9. 单个数值修改线段树（数组A中某一个元素值更新时）

(1) 令Data[L]的值变成y，利用区间更新函数等价于将Data[L]->Data[L]的值都加入value =y-Data[L]

(2) update(1,l,l,value);

\10. 查询区间和querySum函数

(1) 如果区间被覆盖

① 直接返回区间的数据Returnt [p].SUM

(2) 如果区间没有被覆盖

① 执行push_down（P），执行向下更新左右儿子结点的数据

\1) 当lazy不为零的时候，将左右儿子的值利用lazy修改左右儿子的SUM和Max

\2) 将当前p的lazy下传给左右儿子的lazy

\3) 当前p的lazy清零

② 定义mid = t[p].l + t[p].r >> 1;方便后续判断

③ 如果(l <= mid)需要查询左儿子，就加入整理左儿子的数据sum += querySum(lson§,l,r)

④ 如果(r > mid)，如要查询右儿子，就加入整理右儿子的数据sum += querySum(rson§,l,r);

⑤ 返回return sum

\11. 查询区间最大值query_Max函数

(1) 如果区间被覆盖

① 直接return t[p].Max

(2) 如果区间没有被覆盖

① 定义mid = t[p].l + t[p].r >> 1;方便后续判定

② 定义maxL = -inf,maxR = -inf;

③ 如果(l <= mid)需要查询左儿子，则查左儿子的最大值maxL = max(maxL,query_Max(lson§,l,r));

④ 如果(r > mid)需要查询右儿子，则查询右儿子最大值maxR = max(maxR,query_Max(rson§,l,r));

(3) 返回 左右子树的最大值

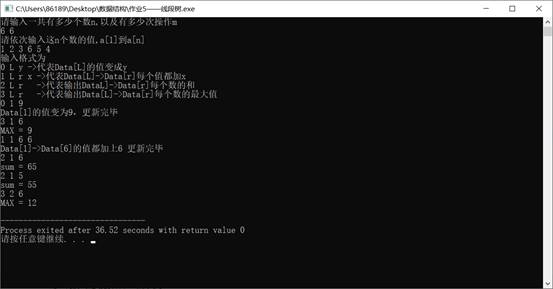
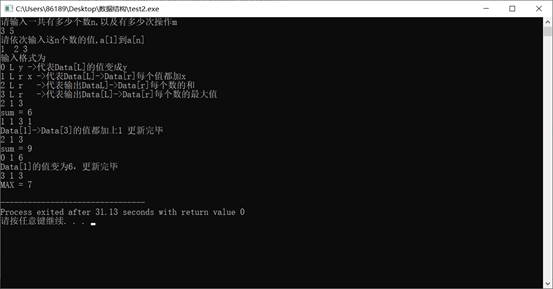
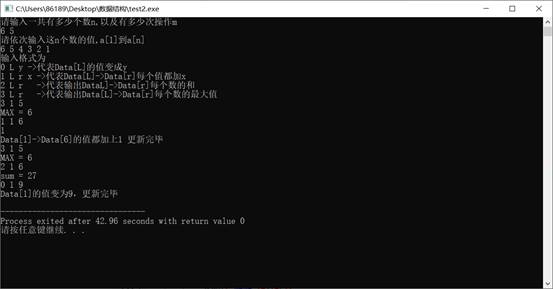
测试样例：img

imgimg

具体代码

\#include<bits/stdc++.h>

using namespace std;

typedef long long ll;

\#define mem(a,x) memset(a,x,sizeof(a))

\#define IOS ios_base::sync_with_stdio(false);cin.tie(NULL);cout.tie(NULL);

const double PI = acos(-1.0);

const ll MAXN = 2e5 + 10;

const ll mod = 998244353;

const ll inf = 1e18;

const ll mo = 1e9+7;

int n,m,mx;

ll Data[MAXN];//代表这每一个区间的一块地点存储的值 

struct TREE

{

  int l,r;//代表节点维护的区间范围;代表了a[l]->a[r] 

  ll SUM; !!!!!!!!!sum总和 

  ll lazy; //涉及lazy标记的东西;

  ll Max;//最大值

}t[MAXN << 2];

inline int lson(int p){return p << 1;}//左儿子;

inline int rson(int p){return p << 1 | 1;}//右儿子;

void build(int p,int l,int r)//建线段树 

{

  t[p].l = l,t[p].r = r;

  if(l == r)//叶子节点

  {

​    t[p].SUM = Data[l];

​    

​    t[p].Max = Data[l];// 

​    return;

  }

  int mid = t[p].l + t[p].r >> 1;

  build(lson(p),l,mid);

  build(rson(p),mid + 1,r);

  t[p].SUM = t[lson(p)].SUM + t[rson(p)].SUM;

  t[p].Max = max(t[lson(p)].Max,t[rson(p)].Max);//递归建树!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!

}

 

void push_down(int p)

{

  if(t[p].lazy)

  {

​    //如果lazy标记不为0

​    t[lson(p)].SUM += t[p].lazy * (t[lson(p)].r - t[lson(p)].l + 1);

​    t[rson(p)].SUM += t[p].lazy * (t[rson(p)].r - t[rson(p)].l + 1);

​          t[lson(p)].Max += t[p].lazy;//!!!!

​          t[rson(p)].Max += t[p].lazy;//!!!!

​    //下传;

​    t[lson(p)].lazy += t[p].lazy;

​    t[rson(p)].lazy += t[p].lazy;

 

​    t[p].lazy = 0;//下传完成,更新lazy为0;

  }

}

void update(int p,int l,int r,ll value)//将区间 [x, y][x,y] 内每个数加上 k

{

  if(l <= t[p].l && r >= t[p].r)//1.区间被覆盖,就修改;

  {

​    t[p].SUM += value * (t[p].r - t[p].l + 1);

​    t[p].Max += value;

​    t[p].lazy += value;

​    return;

  }

  push_down(p);     

  int mid = t[p].l + t[p].r >> 1;

  if(l <= mid)

​          update(lson(p),l,r,value);//覆盖了左儿子就修改左儿子;

​    if(r > mid)

​          update(rson(p),l,r,value);

 

  t[p].SUM = t[lson(p)].SUM + t[rson(p)].SUM;

  t[p].Max = max(t[lson(p)].Max,t[rson(p)].Max);//!!!!!!!!!!!!!!

}

 

ll querySum(int p,int l,int r)//输出区间 [x, y][x,y] 内每个数的和

{

  if(l <= t[p].l && r >= t[p].r)

​          return t[p].SUM;//覆盖了该区间就直接返回整个数据;

 

  push_down(p);

 

  ll sum = 0;

  int mid = t[p].l + t[p].r >> 1;

  if(l <= mid)

​          sum += querySum(lson(p),l,r);

  if(r > mid)

​          sum += querySum(rson(p),l,r);

 

  return sum;

}

ll query_Max(int p,int l,int r)

{

  if(l <= t[p].l && r >= t[p].r)

​          return t[p].Max;

 

  int mid = t[p].l + t[p].r >> 1;

  ll maxL = -inf,maxR = -inf;

  if(l <= mid)maxL = max(maxL,query_Max(lson(p),l,r));

  if(r > mid)maxR = max(maxR,query_Max(rson(p),l,r));

 

  return max(maxL,maxR);

 

}

 

void update_point(int l,ll y)//l y ->代表a[l]的值变成y\n

{//等将于 将区间[l,l]内每个数加上 value = y-a[l] 

​     ll value = y- Data[l];

​     update(1,l,l,value); 

}

int main()

{

​     printf("请输入一共有多少个数n,以及有多少次操作m\n");

  scanf("%d%d",&n,&m);

  printf("请依次输入这n个数的值,a[1]到a[n]\n");

  for(int i = 1;i <= n;i ++)

​          scanf("%lld",&Data[i]);

  build(1,1,n);//建立线段树 a[1]->a[n]

​     //执行操作

​     printf("输入格式为\n");

​     printf("0 L y ->代表Data[L]的值变成y\n");

​     printf("1 L r x ->代表Data[L]->Data[r]每个值都加x\n");

​     printf("2 L r  ->代表输出DataL]->Data[r]每个数的和\n");

​     printf("3 L r  ->代表输出Data[L]->Data[r]每个数的最大值\n");

​     int l,r;

​     ll y;

​     ll value;

  for(int i = 1;i <= m;i ++)

  {

​    int oporate;

​              scanf("%d",&oporate);

​    if(oporate == 0)

​    {

​              scanf("%d",&l);

​              scanf("%lld",&y);

​              value = y-Data[l];

​      update(1,l,l,value);

​      printf("Data[%d]的值变为%lld，更新完毕\n",l,y);

​          }

​    else if(oporate == 1)

​    {

​              scanf("%d%d",&l,&r);

​              scanf("%lld",&value);

​      update(1,l,r,value);

​      printf("Data[%d]->Data[%d]的值都加上%lld 更新完毕\n",l,r,value);

​    }

​    else if(oporate ==2)

​    {

​      scanf("%d%d",&l,&r);

​      printf("sum = %lld\n",querySum(1,l,r));

​    }

​    else

​    {

​         scanf("%d%d",&l,&r);

​         mx = query_Max(1,l,r);//输入l,r，找出a[l]到a[r]的最大值 

​          printf("MAX = %lld\n",mx);//出最大值

​          }

  }

}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/531867.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

深析AutosarNM 网络管理

深析AutosarNM 网络管理

深析AutosarNM 网络管理 深析AutosarNM 网络管理1. AutosarNM 网络管理相关的专业术语2. 各种模式下的各种状态下&#xff0c;报文的收发情况汇总如下表&#xff1a;3. AutosarNM网络管理使用的时间参数&#xff1a;4. AutosarNM网络管理唤醒请求(Wake Up Request)5. ​​​​​…
阅读更多...
MySQL 5.7数据库下载与安装教程

MySQL 5.7数据库下载与安装教程

说明&#xff1a; 安装环境:Win10 64位 软件版本:MySQL 5.7.35 解压版 一.下载 点击下载地址&#xff1a; MySQL :: Download MySQL Community Server (Archived Versions) https://downloads.mysql.com/archives/community/ 选择合适的版本下载 绿色框框 是正式版&#xff0…
阅读更多...
第02讲：SpringCloudStream

第02讲：SpringCloudStream

一、什么是SpringCloudStream SpringCloudStream是SpringCloud的一个子项目&#xff0c;他提供了一套更加通用的操作MQ的解决方案 Destination Binder&#xff08;目标绑定器&#xff09; &#xff1a;微服务与消息中间件通信的组件Destination Bindings&#xff08;目标绑定&…
阅读更多...
2023爱分析･云原生 IDE 市场厂商评估报告-行云创新（CloudToGo)

2023爱分析･云原生 IDE 市场厂商评估报告-行云创新（CloudToGo)

1. 研究范围定义 企业数字化转型初期&#xff0c;通过资源池云化&#xff0c;解决了IDC时代运维、部署、扩容的难题&#xff0c;但传统应用单体架构厚重、烟囱式架构等带来的一系列应用层面的问题并没有得到有效解决&#xff0c;云对业务的价值主要还停留在资源供给的阶段…
阅读更多...
Scaled dot-prodect Attention的原理和实现（附源码）

Scaled dot-prodect Attention的原理和实现（附源码）

文章目录 背景什么是AttentionAttention权重的计算方法1. 多层感知机法2. Bilinear方法3. Dot Product4. Scaled Dot Product Scaled dot-prodect Attention的源码实现 背景 要了解深度学习中的Attention&#xff0c;就不得不先谈Encoder-Decoder框架&#xff08;sequence to s…
阅读更多...
拍立淘API接口说明文档 按图搜索淘宝商品API 实时数据返回

拍立淘API接口说明文档 按图搜索淘宝商品API 实时数据返回

开发背景&#xff1a; 随着电商行业的不断发展&#xff0c;人们的购物需求日益增多。在购买商品时&#xff0c;很多人会通过搜索引擎、社交媒体等手段来获取信息或灵感。但是&#xff0c;在这些渠道中找到想要的商品并不容易&#xff0c;因为其中可能会混杂着一些广告或无关内…
阅读更多...
Android内存优化检测工具LeakCanary使用

Android内存优化检测工具LeakCanary使用

一、什么是LeakCanary leakCanary是Square开源框架&#xff0c;是一个Android和Java的内存泄露检测库。如果检测到某个activity有内存泄露&#xff0c;LeakCanary就是自动地显示一个通知&#xff0c;所以可以把它理解为傻瓜式的内存泄露检测工具。通过它可以大幅度减少开发中遇…
阅读更多...
Java 并发队列详解

Java 并发队列详解

一&#xff0c;简介 1&#xff0c;并发队列两种实现 以ConcurrentLinkedQueue为代表的高性能非阻塞队列以BlockingQueue接口为代表的阻塞队列 2&#xff0c;阻塞队列与非阻塞队列的区别 当阻塞队列是空的时&#xff0c;从队列中获取元素的操作将会被阻塞&#xff0c;试图从…
阅读更多...
【BFS】华子20230506笔试第三题（动态迷宫问题）Java实现

【BFS】华子20230506笔试第三题（动态迷宫问题）Java实现

文章目录 题目链接思路BFS板子我的解答 题目链接 塔子哥的codeFun2000&#xff1a;http://101.43.147.120/p/P1251 测试样例1 输入 3 2 1 0 1 2 2 1 2 0 100 100 100 100 000 100 000 000 001输出 1测试样例2 输入 3 2 1 0 2 0 0 1 2 2 000 000 001 010 101 101 110 010 …
阅读更多...
在docker容器中启动docker服务并实现构建多平台镜像的能力

在docker容器中启动docker服务并实现构建多平台镜像的能力

在docker容器中启动docker服务并实现构建多平台镜像的能力 背景 在容器中运行docker&#xff0c;是devops中无法避免的场景&#xff0c;通常被应用于提供统一的镜像构建工具&#xff0c;出于安全考虑&#xff0c;不适合将主机的docker进程暴露给公司的内部人员使用&#xff0…
阅读更多...
SpringCloud alibaba微服务b2b2c电子商务平台

SpringCloud alibaba微服务b2b2c电子商务平台

1. 涉及平台 平台管理、商家端&#xff08;PC端、手机端&#xff09;、买家平台&#xff08;H5/公众号、小程序、APP端&#xff08;IOS/Android&#xff09;、微服务平台&#xff08;业务服务、系统服务、中间件服务&#xff09; 2. 核心架构 Spring Cloud、Spring Boot2、My…
阅读更多...
飞书开发流程

飞书开发流程

1、进入飞书并创建一个应用 链接: 创建应用 创建应用成功后需要审核通过&#xff0c;如果你拥有管理权限则可以自己进入管理后台通过审核&#xff0c;否则需要联系管理员通过审核 2、进入开发者后台 链接: 发者后台 3、在该调试平台上测试 以这个订阅审批事件为例 这一步…
阅读更多...
DHCP协议简单配置

DHCP协议简单配置

实验原理 网络中主机需要与外界进行通信时，需要配置自己的IP地址、网关地址、DNS服务器等网络参数信息。手工在每台主机上配置维护成本高，容易出错，而且不利于管理员统一维护。 通过DHCP地址自动配置协议，使终端设备能自动获取地址，实现即插即用且IP地址统一由服务器管理…
阅读更多...
springboot+java充电桩充电额维修管理系统

springboot+java充电桩充电额维修管理系统

项目介绍 Spring Boot 是 Spring 家族中的一个全新的框架&#xff0c;它用来简化Spring应用程序的创建和开发过程。也可以说 Spring Boot 能简化我们之前采用SSM&#xff08;Spring MVC Spring MyBatis &#xff09;框架进行开发的过程。 系统基于B/S即所谓浏览器/服务器模式…
阅读更多...
STM32 学习笔记_9 定时器中断：编码器接口模式

STM32 学习笔记_9 定时器中断：编码器接口模式

TIM编码器接口 之前我们处理旋转编码器&#xff0c;是转一下中断一次&#xff0c;挺消耗资源的。 我们可以利用TIM的编码器功能&#xff0c;隔一段时间取一下旋转器值使得cnt或–&#xff0c;以此判断旋转位置以及计算速度&#xff0c;相比中断节约资源。相当于外接了一个有方…
阅读更多...
Kubernetes那点事儿——暴露服务之Service

Kubernetes那点事儿——暴露服务之Service

Kubernetes那点事儿——暴露服务之Service 前言一、Service二、Service与Pod关系三、Service常用类型ClusterIPNodePortLoadBalancer 四、Service代理模式IptablesIPVS修改代理模式 前言 K8s中&#xff0c;我们将应用跑在Pod里。多数情况下是一组Pod&#xff0c;用户如何访问这…
阅读更多...
凌恩生物美文分享 | 提升科研有一套 | 宏基因组磷循环分析又出新！

凌恩生物美文分享 | 提升科研有一套 | 宏基因组磷循环分析又出新！

磷是包括微生物在内的所有生命体中不可缺少的元素。在生物大分子核酸、高能量化合物ATP、以及生物体内糖代谢的某些中间体中&#xff0c;都有磷的存在。在自然界中&#xff0c;磷的循环包括可溶性无机磷的同化、有机磷的矿化、不溶性磷的溶解等。微生物分解含磷化合物的作用&am…
阅读更多...
操作系统面试相关知识

操作系统面试相关知识

目录 一、简介1、什么是操作系统2、操作系统主要有哪些功能&#xff1f; 二、操作系统结构1、什么是内核&#xff1f;2、什么是用户态和内核态&#xff1f;3、 用户态和内核态是如何切换的&#xff1f; 三、 进程和线程1、并行和并发有什么区别&#xff1f;2、什么是进程上下文…
阅读更多...
无线传感器网络的时钟同步估计问题（Matlab代码实现）

无线传感器网络的时钟同步估计问题（Matlab代码实现）

目录 &#x1f4a5;1 概述 &#x1f4da;2 运行结果 &#x1f389;3 参考文献 &#x1f468;‍&#x1f4bb;4 Matlab代码 &#x1f4a5;1 概述 随着无线传感器网络的快速发展,其应用领域也越来越广。在诸多的应用环境中都需要大量已同步的传感器节点通过协同作用执行一个…
阅读更多...
Python 中IndexError: list assignment index out of range 错误解决

Python 中IndexError: list assignment index out of range 错误解决

文章目录 Python IndexError&#xff1a;列表分配索引超出范围修复 Python 中的 IndexError: list assignment index out of range修复 IndexError: list assignment index out of range 使用 append() 函数修复 IndexError: list assignment index out of range 使用 insert()…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023